-
Плазменное состояние вещества. Уравнение Власова. Понятие о самосогласованном поле.
Приблизительное определение: плазма – квазинейтральный ионизированный газ, состоящий из большого количества положительно и отрицательно заряженных частиц, а в ряде случаев из нейтральных атомов и молекул.
Параметры плазмы:
-
концентрация
(плотность) частиц разного сорта (
);
-
степень
ионизации
;
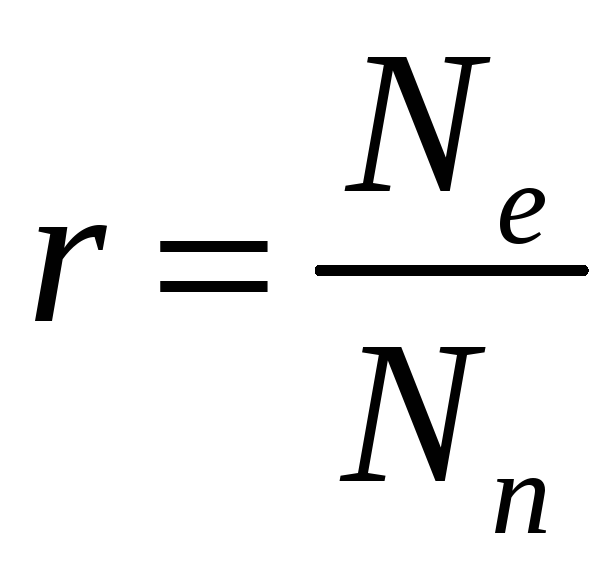- заряд и масса частиц;
- температура плазмы.
Условие квазинейтральности: газ (плазма) в среднем за достаточно большие промежутки времени и на достаточно больших расстояниях должен быть в целом нейтральным.
Временной
масштаб разделения зарядов:
,
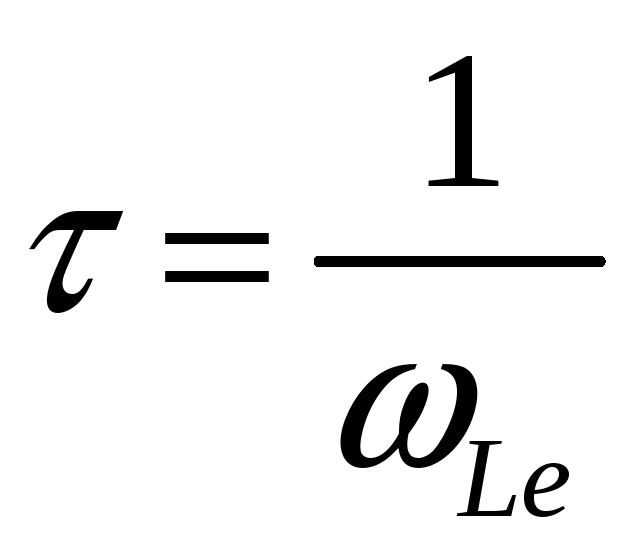где
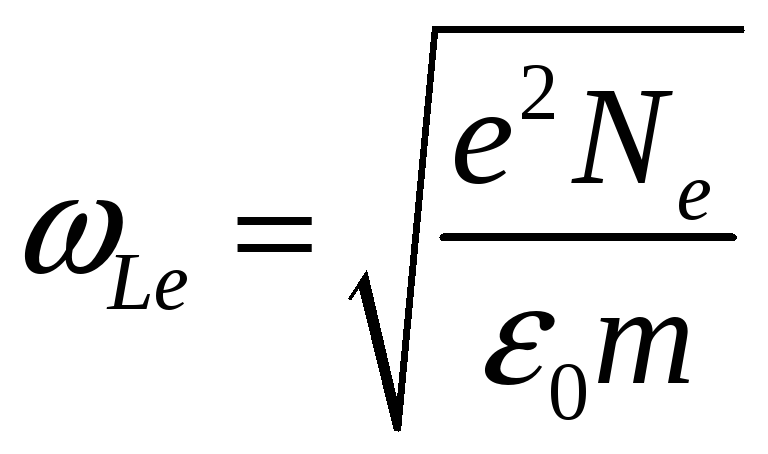– плазменная частота. При
частицы совершают много колебаний около
положения равновесия.
Пространственный
масштаб разделения зарядов:
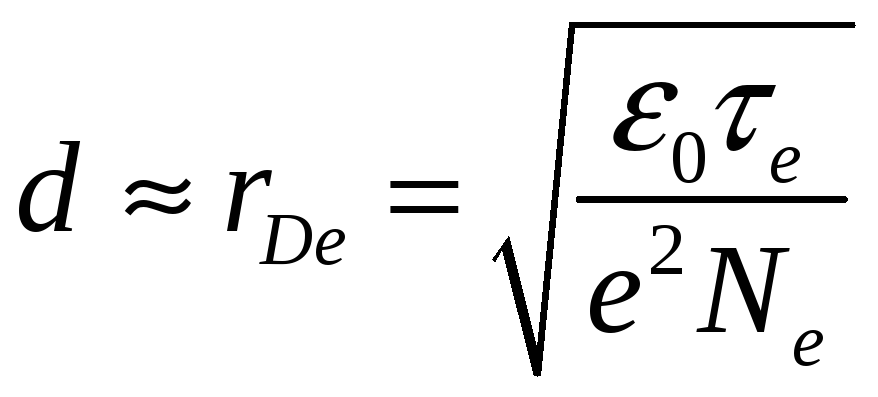– электронный дебаевский радиус.
Условие
квазинейтральности:
характерные размеры
.
Для
вывода ур-я Власова используем
статистическое описание системы частиц:
вводится ф-я распределения, характеризующая
вероятность нахождения частицы в
определенном состоянии в момент времени
в заданной точке пр-ва
.
Если состояние частицы сорта
характеризуется импульсом
и её энергия
однозначно определяется этим импульсом,
то функция распределения имеет вид
.
Величина
представляет число частиц сорта
в момент времени
в фазовом интервале
,
а плотность частиц в точке
:
– условие
нормировки.
Зная функцию распределения, можно найти средние значения, например:
,
.
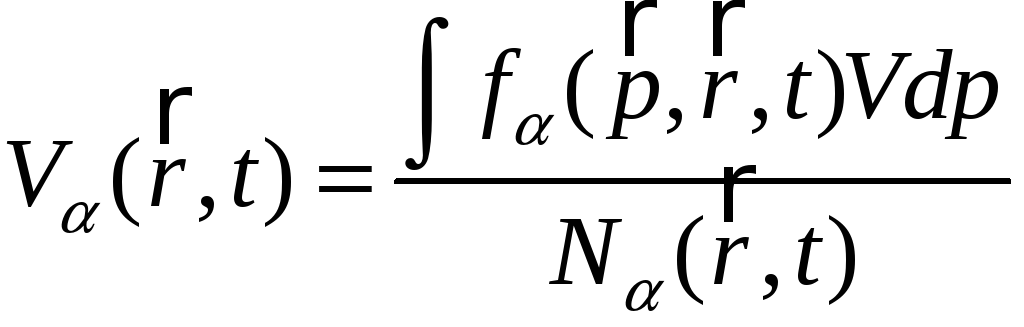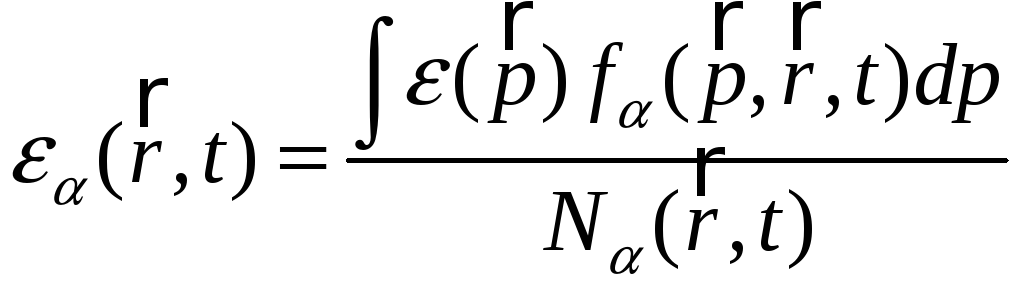Если
в объёме не происходит рождения и гибели
частиц, то функция
не изменяется во времени и
(1)
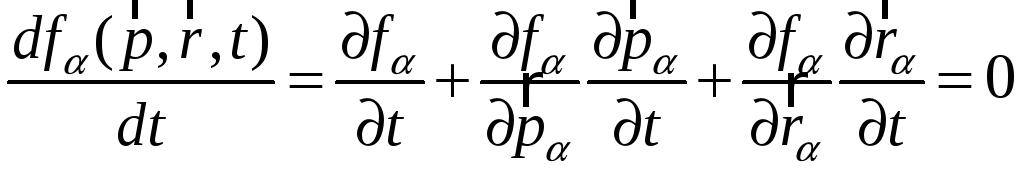– уравнение
непрерывности (Лиувилля).
Согласно
ур-м движения частиц:
,
.
Тогда из (1) следует:
.
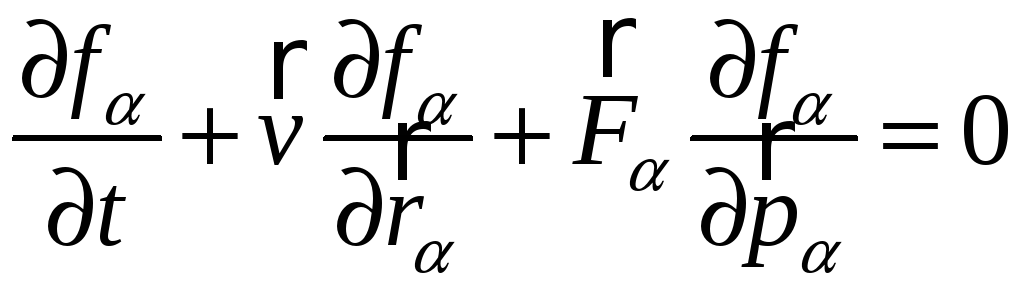– сила,
действующая на частицу сорта
.
В случае заряженных частиц
,
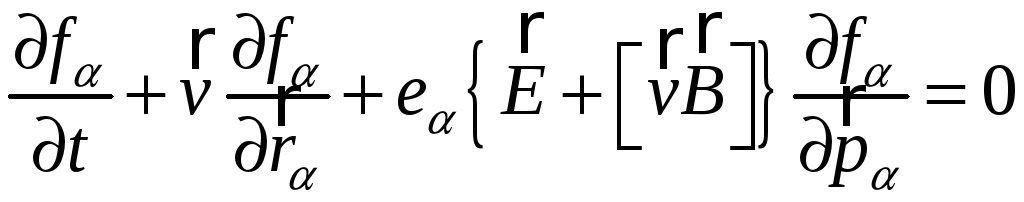– уравнение
Власова.
– электрическое
и магнитное поля в точке нахождения
частицы. Их можно определить из ур-й
Максвелла:
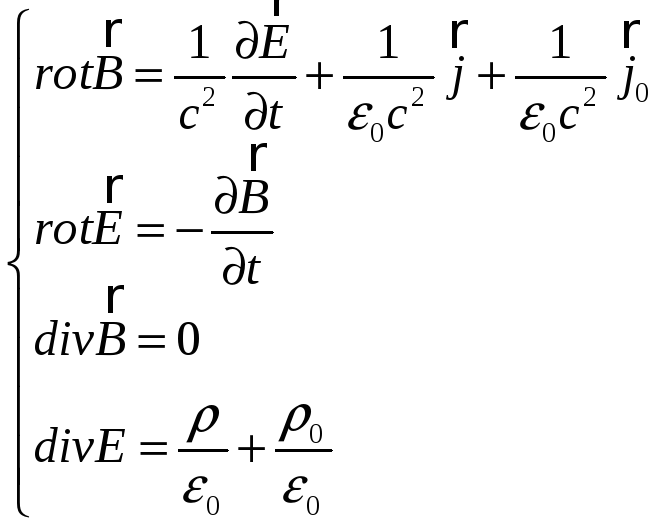
Здесь
и
– плотность тока и заряда, индуцируемых
в среде.
и
– плотность тока и заряда внешних
источников,
– скорость света.
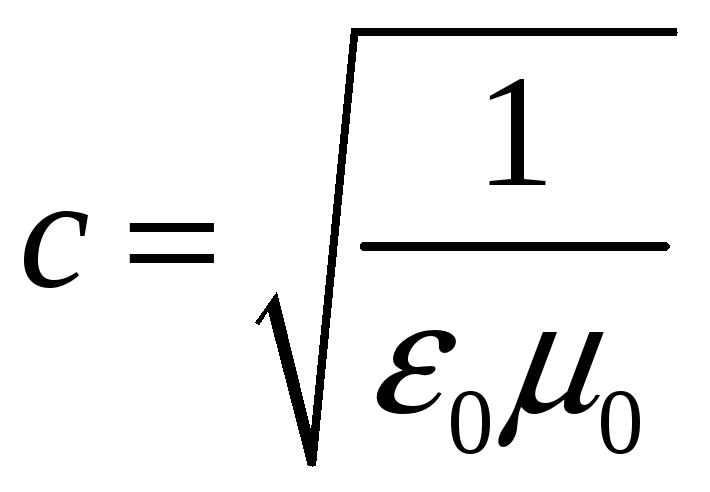и
,
.
Введённые
таким образом поля
и
,
являются самосогласованными, поскольку
из ур-я Власова получается такое
распределение частиц
,
которое вызывает появление э/м полей,
поддерживающих это распределение.