14. Явления переноса.

Теплопроводность: перенос теплоты. Теплопроводность не зависит от давления и увеличивается пропорционально корню квадратному из температуры. В этом случае (см. вопрос про вязкость) есть средняя энергия теплового движения, приходящаяся на одну молекулу. Плотность потока теплоты:.

Коэффициент теплопроводности: ,

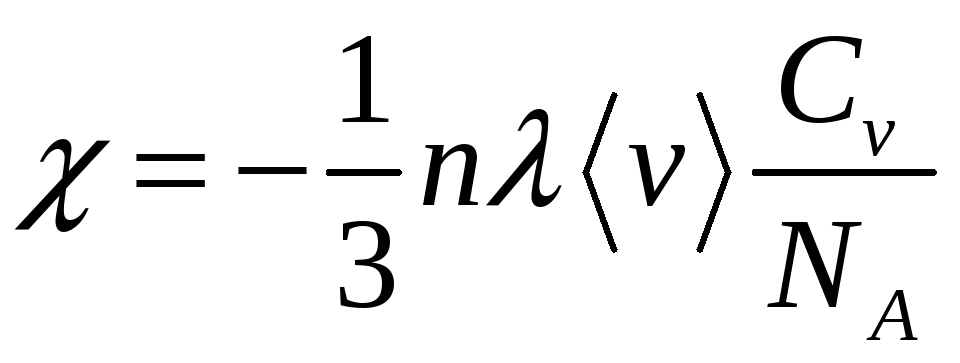– концентрация, – молярная теплоёмкость ( – число степеней свободы), – длина свободного пробега.

Замечания: 1) 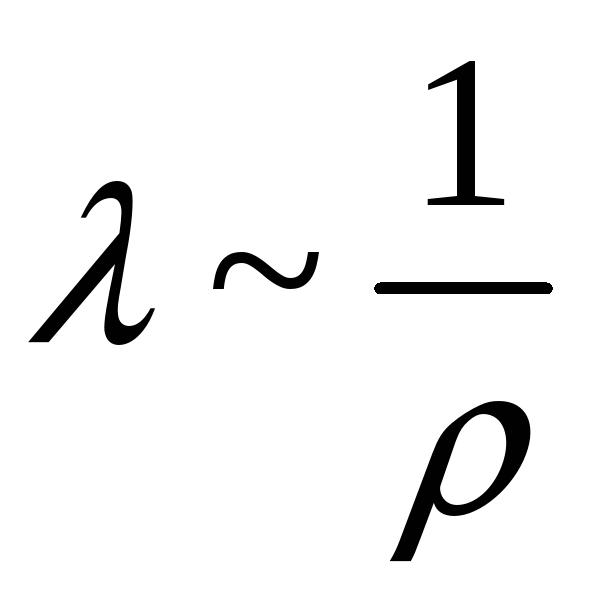, не зависит от давления; 2) .

Диффузия: движение вещества компонент, составляющих фазу, связанное с отклонением плотности системы. – плотность диффузионного потока (кол-во вещ-ва, проходящего перпендикулярно единице площади в ед. времени). – закон Фика.

Коэффициент диффузии: 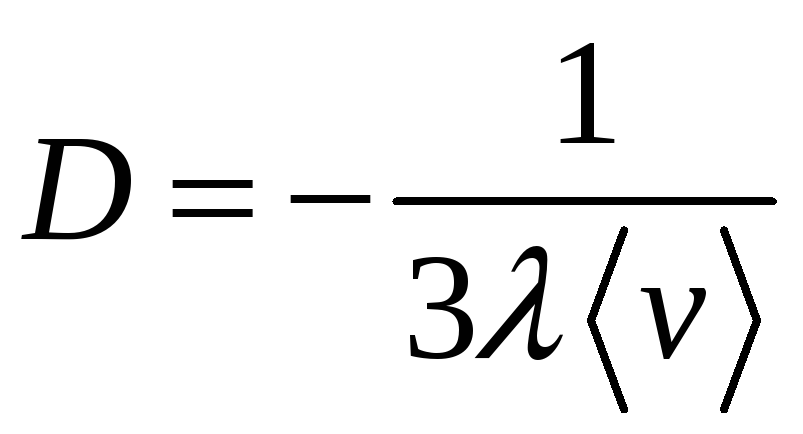, – длина свободного пробега, – средняя скорость.

Замечания: 1) 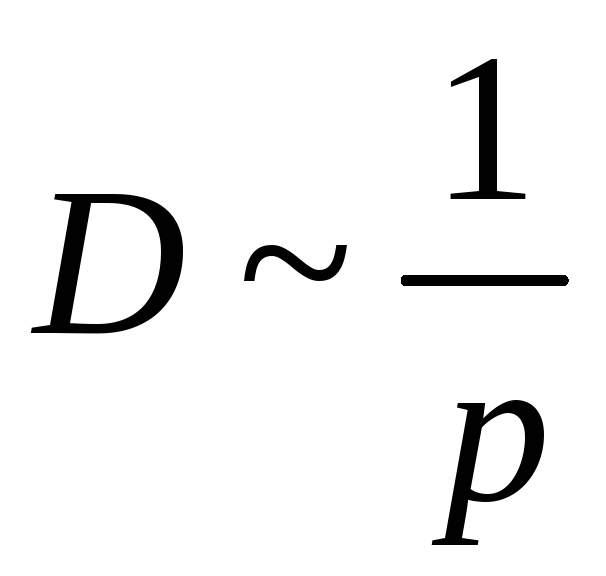, – давление; 2) .

Вязкость: возникновение сил трения в газах и жидкостях обусловлено процессом переноса импульса упорядоченным движеним молекул. Быстрее движущийся слой замедляется, а медленнее движущийся – ускоряется. . Кинематическая вязкость – динамическая вязкость, отнесённая к плотности.

Пусть характеризует некоторое молекулярное свойство, отнесённое к одной молекуле. Этим свойством может быть энергия, импульс, концентрация. Если в равновесном состоянии постоянно по всему объёму, то при наличии градиента имеет место движение в направлении его уменьшения. Пусть ось направлена вдоль градиента . Среднее расстояние, пробегаемое молекулами, пересекающими площадку после последнего столкновения, равно 2<l>3. – импульс, передаваемый в единицу времени от слоя к слою через единицу поверхности, т.е. плотность потока импульса.

, – скорость движения газа как целого.

.

Замечания: 1) не зависит от давления; 2) .

Потоки всех величин являются алгебраическими. Их знак зависит от направления оси . Достаточно обратить направление этой оси на противоположное, и знак потока изменится.

Во всех явлениях переноса направления плотностей потоков противоположны градиентам соответствующих величин. Это означает, что потоки всегда направлены в сторону уменьшения величин , , , т.е. против их градиентов. Таким образом, для потоков существенны градиенты величин, имеющих тенденцию выравниваться.

15. Кинетическое Уравнение Больцмана. Понятие об н-теореме Больцмана.

Задача: найти уравнение для интеграла столкновения частиц.

Предположения:

I. Рассматриваем только парные взаимодействия, где радиус действия 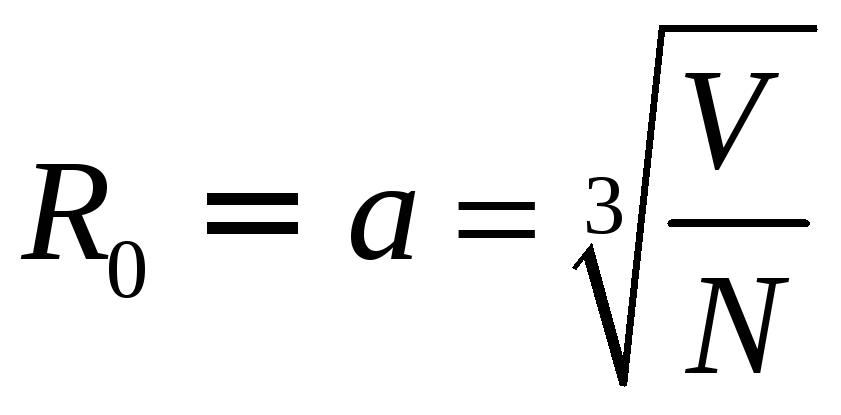, время столкновения – рассматриваем пространственно однозначные системы. .

II. Решение будем искать виде статистических функций , т.е. функций, определяющих число частиц в объёме . Исходить будем из первого ур-я цепочки Боголюбова (также можно получить из законов сохр. энергии и импульса).

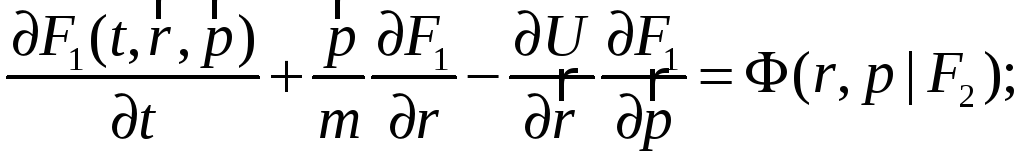
(1) зависит от через зависимость от .

Пусть 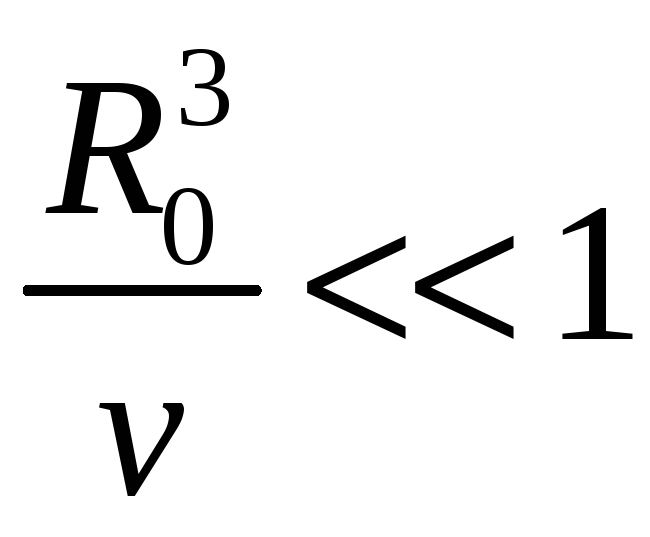, используем принцип ослабления:

(2) ; . Запишем ур-е Лиувилля для 2-х частиц:

(3) .

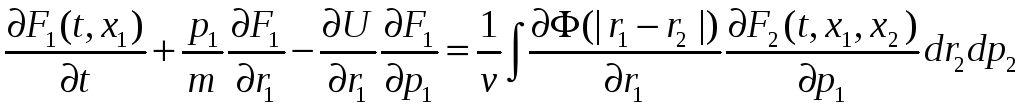(4) .

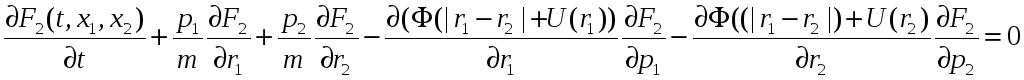Далее используем условие эволюции; полагая , . Упрощая (4) и подставляя выражение для в (3).

Интеграл столкновения (кинетическое ур-е) Больцмана:

(5)

Н-теорема Больцмана.

Введём: и .

Исследуем знаки производных и . После преобразований придем к неравенству:

.

Уравнение Больцмана описывает необратимую во времени эволюцию системы.