- •Молекулярная физика.
- •Термодинамический подход к описанию молекулярных явлений.
- •Первое начало термодинамики. Циклические процессы
- •Второе начало термодинамики.
- •Энтропия термодинамической системы. Термодинамические потенциалы.
- •Взаимодействие молекул. Идеальный газ. Основные газовые законы.
- •1. Дискретный спектр энергий :
- •2. Распределение Гиббса.
- •3. Большое каноническое распределение (для ):
- •Теория флуктуаций. Броуновское движение.
- •Реальные газы. Уравнение Ван-дер-Ваальса.
- •Твердые тела. Кристаллы. Симметрия кристаллов.
- •Фазовые переходы первого и второго рода. Условия устойчивости и равновесия.
- •Явления переноса.
- •Кинетическое Уравнение Больцмана. Понятие об н-теореме Больцмана.
- •Плазменное состояние вещества. Уравнение Власова. Понятие о самосогласованном поле.
-
Теория флуктуаций. Броуновское движение.
-
Реальные газы. Уравнение Ван-дер-Ваальса.
Для
идеальных газов уравнение Клапейрона:
![]() .
Для реальных газов оно соблюдается лишь
приближенно. Отступления от идеальной
модели связаны с наличием жидкого и
твердого состояний и наличием
межмолекулярного взаимодействия.
.
Для реальных газов оно соблюдается лишь
приближенно. Отступления от идеальной
модели связаны с наличием жидкого и
твердого состояний и наличием
межмолекулярного взаимодействия.
Потенциал
взаимодействия (Леннарда-Джонса):
![]() .
.
Здесь
![]() – константы,
– константы,
![]() – расстояние между центрами
взаимодействующих частиц. Этот потенциал
с хорошей точностью описывает реальный
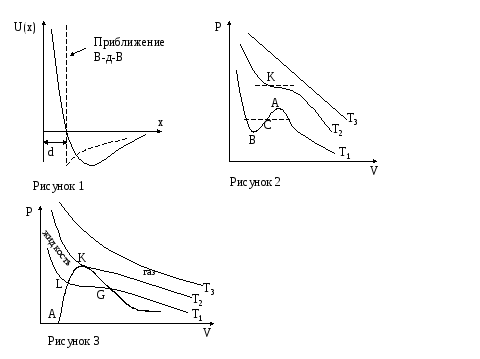
газ. На рисунке 1
– расстояние между центрами
взаимодействующих частиц. Этот потенциал
с хорошей точностью описывает реальный
газ. На рисунке 1
![]() – диаметр молекулы. Рассматриваемая
модель газа: твердые упруго сталкивающиеся
шары, причем возможны только парные
столкновения (это выполняется довольно
точно при небольших давлениях газа).
– диаметр молекулы. Рассматриваемая
модель газа: твердые упруго сталкивающиеся
шары, причем возможны только парные
столкновения (это выполняется довольно
точно при небольших давлениях газа).
Уравнение
Ван-дер-Ваальса
![]() ,
,
где
![]() – универсальная газовая постоянная,
– универсальная газовая постоянная,
![]() – давление,
– давление,
![]() – объем,
– объем,
![]() – температура,
– температура,
![]() – поправка на то, что отдельно взятой
молекуле предоставлен не весь объем
– поправка на то, что отдельно взятой
молекуле предоставлен не весь объем
![]() ,
т.к. молекулы не могут сблизиться на
расстояние, меньшее
,
т.к. молекулы не могут сблизиться на
расстояние, меньшее
![]() ;
;
![]() – поправка на то, что на пристеночный
слой газа действует сила со стороны
всего газа, стремящаяся втянуть внутрь
газа пристеночный слой.
– поправка на то, что на пристеночный
слой газа действует сила со стороны
всего газа, стремящаяся втянуть внутрь
газа пристеночный слой.
![]() – так
называемое внутреннее
давление.
– так
называемое внутреннее
давление.
![]() или
или
![]() ,
,
где
![]() – концентрация,
– концентрация,
![]() – масса частицы,
– масса частицы,
![]() – скорость частицы. Для
– скорость частицы. Для
![]() можно получить:
можно получить:
![]() .
.
Теоретический вывод уравнения Ван-Дер-Ваальса применим при условях:
![]() .
.
В
случае плотных газов уравнение
Ван-Дер-Ваальса лишь качественно
описывает поведение газа. Для реальных
газов
![]() и
и
![]() зависят от температуры.
зависят от температуры.
Изотермы Ван-Дер-Ваальса (рисунок 2).
![]() .
Здесь при
.
Здесь при
![]() наблюдается критическая изотерма, т.е.
при
наблюдается критическая изотерма, т.е.
при
![]() уравнение изотермы имеет один корень
при
уравнение изотермы имеет один корень
при
![]() .
Точка
.
Точка
![]() называется критической.
называется критической.
![]() ,
, ![]() ,
, ![]() .
.
Уравнение изотермы:
![]()
Участки типа ВСА соответствуют неустойчивому состоянию вещества и практически не могут быть реализованы.
Изотермы реального газа (рисунок 3).
Область
между кривой ALKG
и изобарой
![]() соответствует двухфазным состояниям
вещества, т.е. каждая точка этой области
изображает такое состояние вещества,
в котором оно не является физически
однородным, а состоит из жидкости и ее
насыщенного пара (за исключением случаев
неустойчивого состояния в виде перегретой
жидкости или пересыщенного пара).
соответствует двухфазным состояниям
вещества, т.е. каждая точка этой области
изображает такое состояние вещества,
в котором оно не является физически
однородным, а состоит из жидкости и ее
насыщенного пара (за исключением случаев
неустойчивого состояния в виде перегретой
жидкости или пересыщенного пара).
-
Твердые тела. Кристаллы. Симметрия кристаллов.
Твердое состояние возникает при столь сильном взаимодействии между молекулами, что их тепловое движение не играет в структуре значительной роли.
Молекулы располагаются друг относительно друга в фиксированных точках, совершая малые тепловые колебания около положения равновесия. Взаимное расположение молекул повторяется при переходе из одних областей в другие → имеем периодическую структуру, что реализуется в виде кристаллической решетки.
Точки равновесия молекул – узлы кристаллической решетки.
Аморфные тела не находятся в состоянии равновесия.
Примитивная решетка (решетка Браве):
![]() ,
,
![]() – целые
числа,
– целые
числа,
![]() – базисные вектора элементарной ячейки.
– базисные вектора элементарной ячейки.
Некоторая произвольная решетка, вообще говоря, не может быть представлена в виде одной решетки Браве, а является совокупностью решеток Браве.
Браве показал, что можно всегда найти такую примитивную ячейку, которая имеет те же элементы симметрии, что и решетка в целом (кроме гексагональных).
Замечание: под симметрией понимается совокупность элементов симметрии.
Элементы симметрии:
-
ось n-го порядка – нет изменений при повороте на
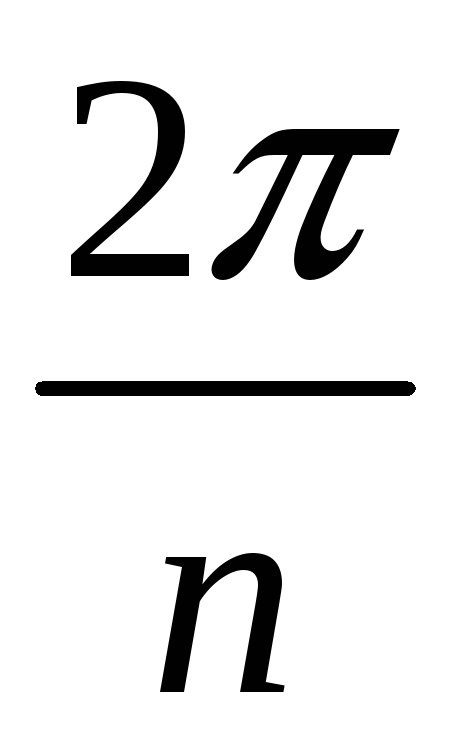 .
.
-
плоскость симметрии – совмещение в результате зеркального отражения.
-
центр симметрии – тело совмещается с собой при повороте отн. точки.
-
Зеркально-поворотная ось n-го порядка – поворот на
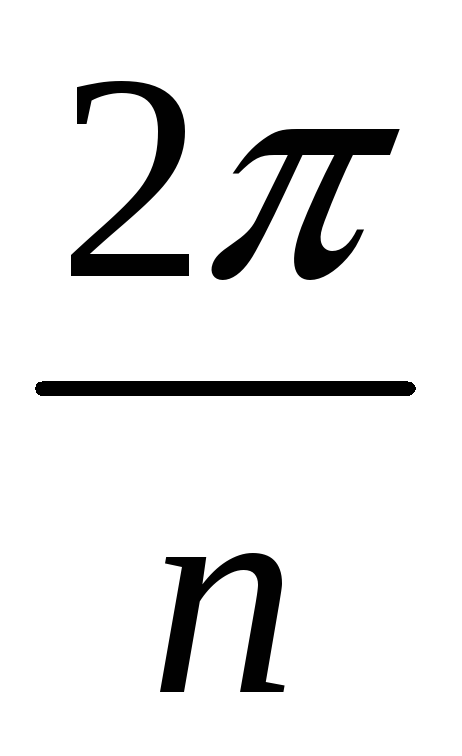 и зеркальная симметрия.
и зеркальная симметрия.
У кристаллической решетки возможна ось вращения 2, 3, 4 и 6-го порядков.
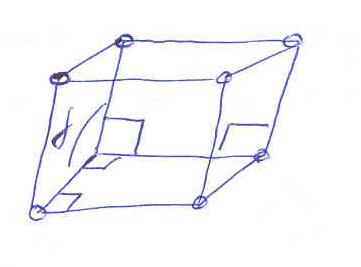
Наименьшая из примитивных ячеек называется параллелепипедом Браве. Существует 6 типов пар. Решетки Браве и гексагональная → 7 типов:
-
Триклинная:
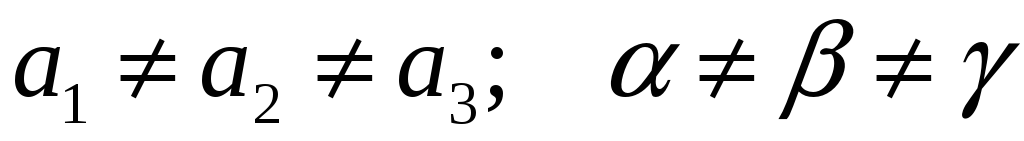
-
Моноклинная:
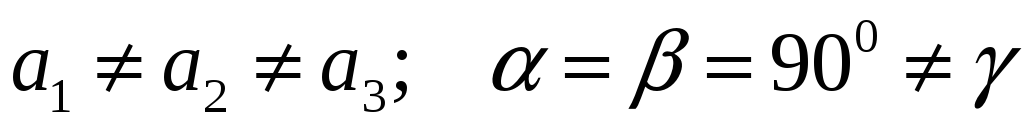
-
Ромбическая:
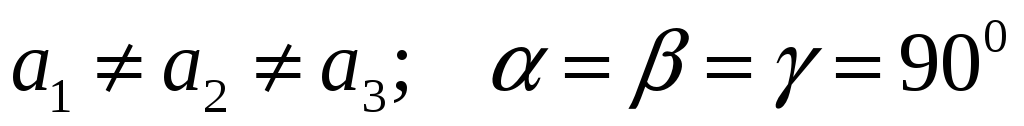
-
Тетрагональная:
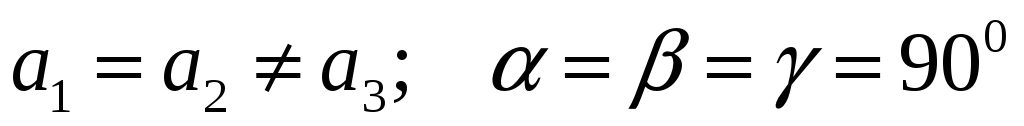
-
Кубическая:
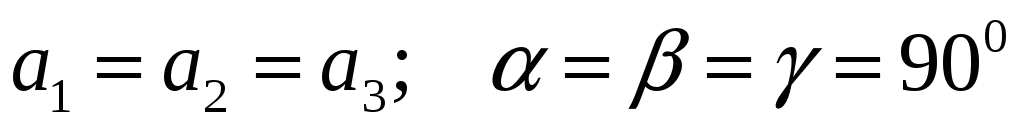
-
Ромбоэдрическая:
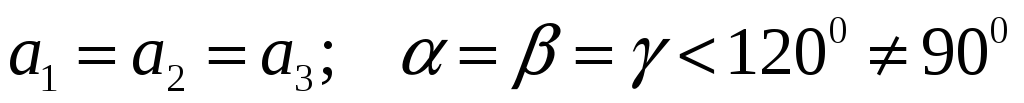
-
Гексагональная:
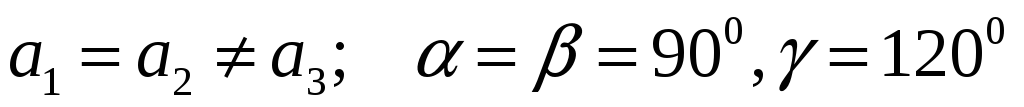 .
.
Триклинная Моноклинная Ромбическая
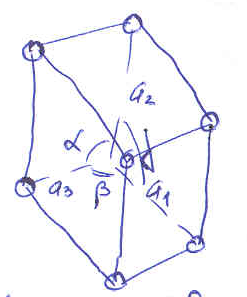
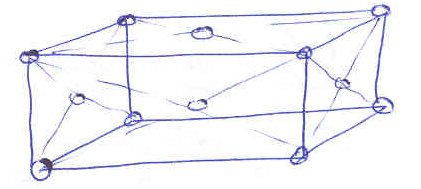
Т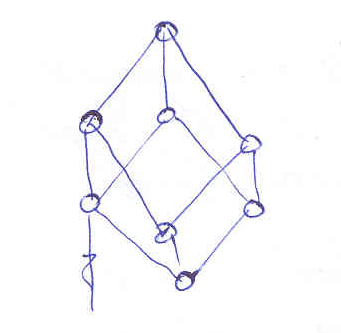 етрагональная Кубическая Ромбоэдрическая
етрагональная Кубическая Ромбоэдрическая
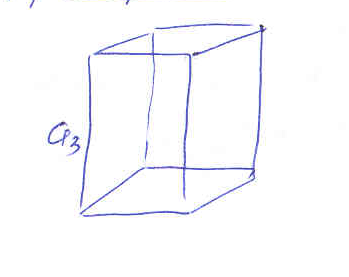
Гексагональная