4. Энтропия термодинамической системы. Термодинамические потенциалы.

Для необратимых круговых процессов выполняется неравенство Клаузиуса, а для обратимых круговых процессов выполняется равенство Клаузиуса: «Приведённое кол-во теплоты, полученное системой при любом квазистатическом круговом процессе, равно нулю».

Энтропия: Энтропия системы есть функция её состояния, определённая с точностью до произвольной постоянной. Разность энтропии в двух равновесных состояниях 2 и 1, по определению, равна приведённому кол-ву теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.

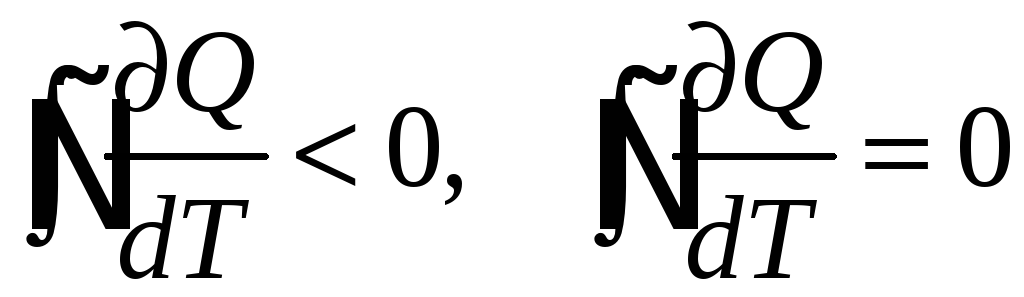
– полный дифференциал

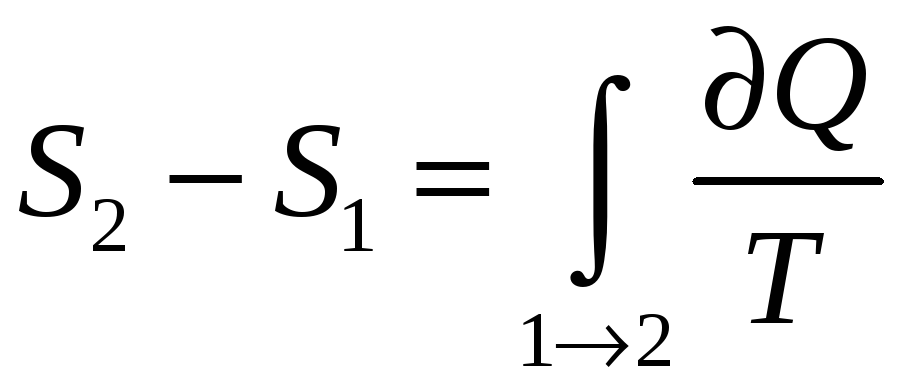, где 1 – необратимый процесс, а 2 – обратимый

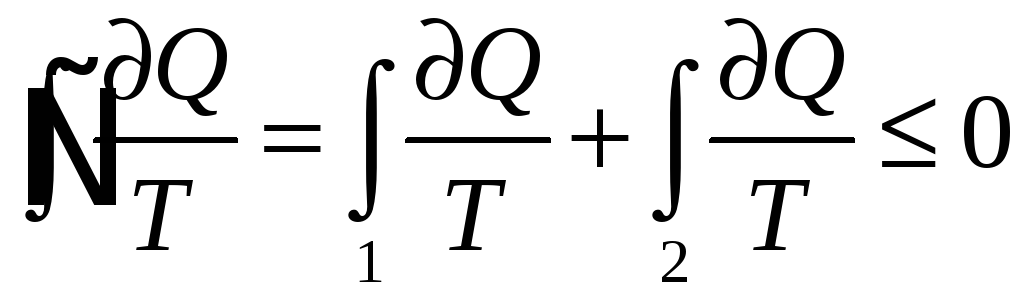
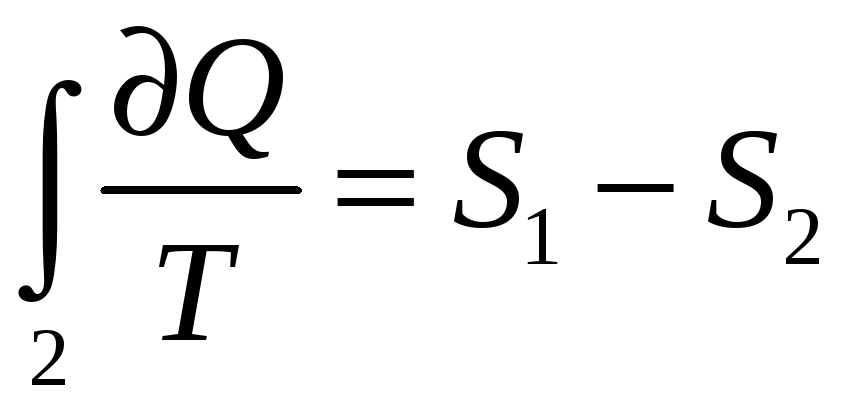, т.к. процесс 2 – квазистатический.

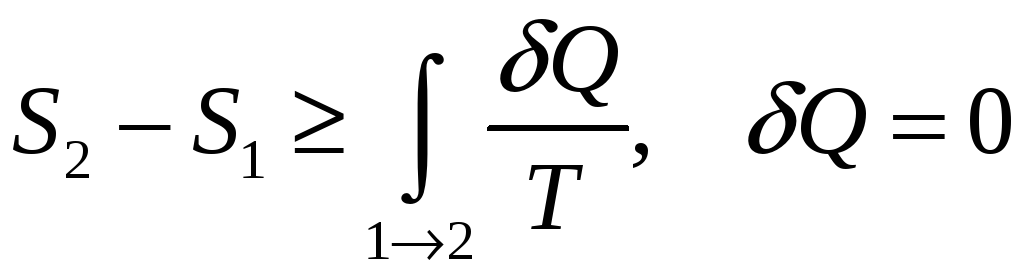, т.к. процесс – адиабатический

Закон возрастания энтропии: энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остаётся постоянной.

Энтропия – аддитивная функция состояния. При расширении в пустоту энтропия увеличивается. Энтропия максимальна в состоянии равновесия.

Энтропия определяется логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние:

– формула Больцмана.

Термодинамические потенциалы.

.

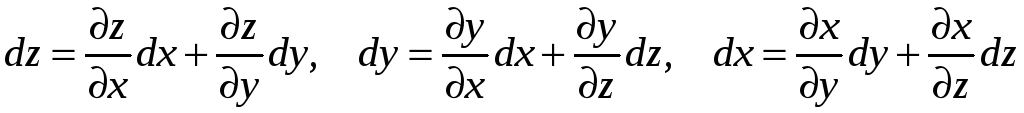
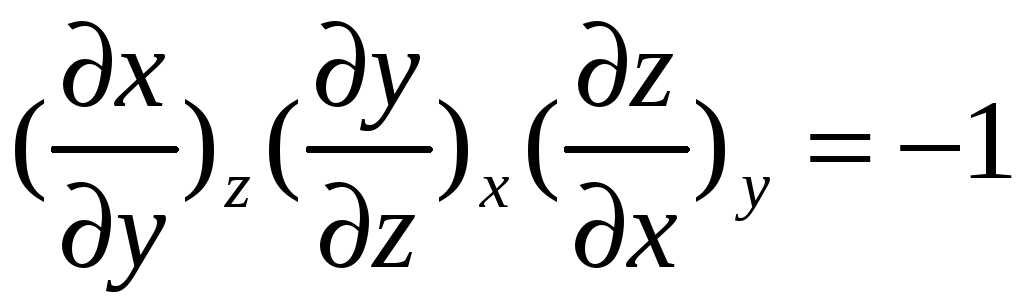Если , то

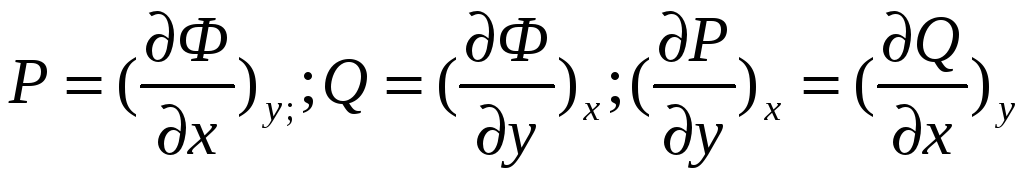
– термодинамическое тождество.

Энтальпия:

Энтропия:

Свободная энергия:

Т/Д функция Гиббса:

5. Взаимодействие молекул. Идеальный газ. Основные газовые законы.

Столкновения делятся на упругие и неупругие.

U – потенциальная энергия взаимодействия частиц: .

Идеальный газ – это такая модель газа, для которой выполняется:

1) U = 0;

2) столкновения между молекулами газа – упругие;

3) молекулы газа – материальные точки.

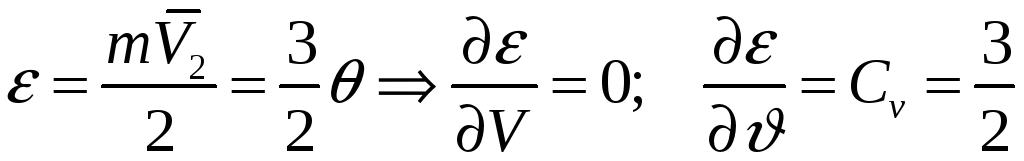_, – внутренняя энергия.

Уравнения состояния: (Клапейрона-Менделеева):

, , , ,

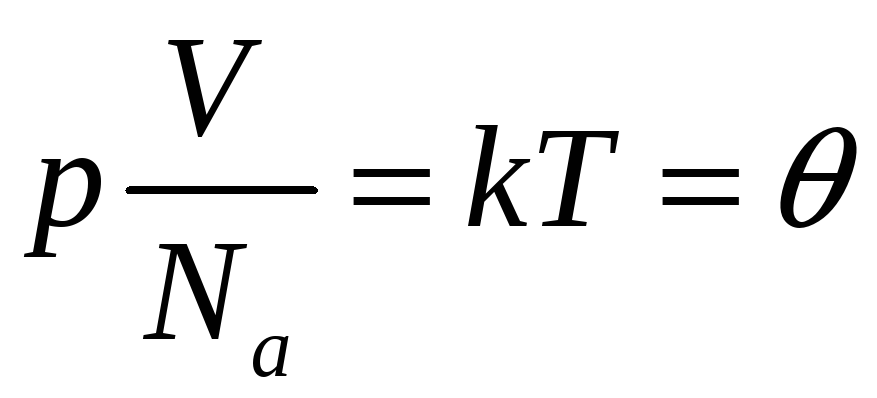Газовые законы:

1) – закон Бойля-Мариотта

2) 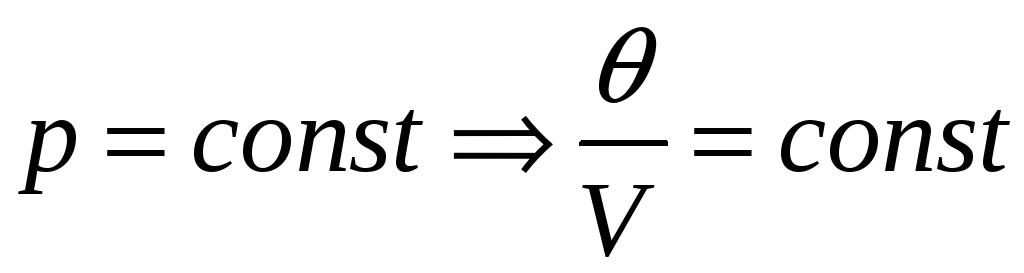– закон Гей-Люссака

3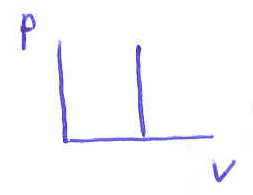) 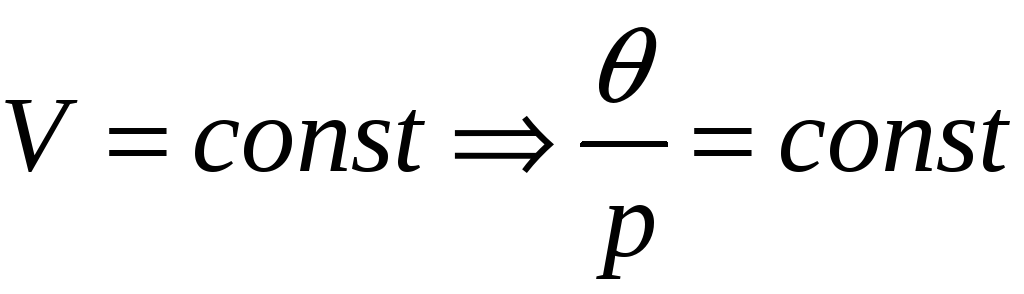– закон Шарля.

6. Распределение молекул газа по скоростям. Идеальный газ во внешнем потенциальном поле.

Распределение Максвелла:

.

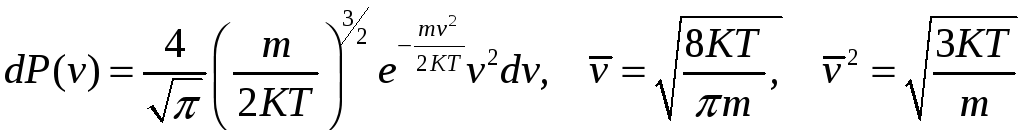Распределение Больцмана.

Путь – потенциал внешнего поля.

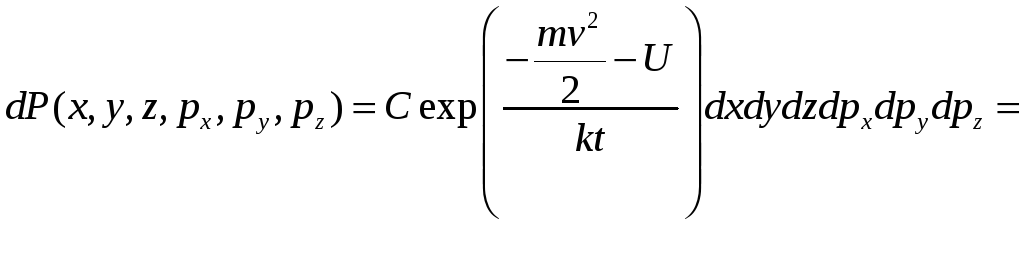
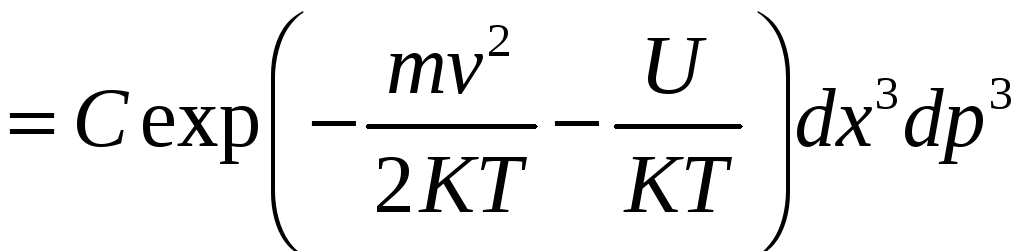, где n – число частиц.

Тогда получится:

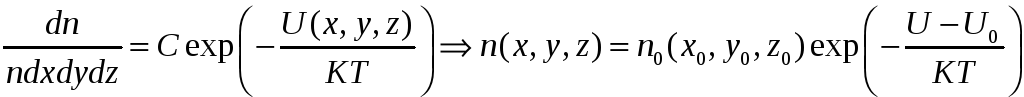
– это и есть распределние Больцмана

7. Канонические распределения.

Пусть есть система с энергией , числом частиц, и параметром .

1. Дискретный спектр энергий :

В этом случае

,

где – квазикронекеровская функция, n – микрокопическое состояние,

– статистический вес.

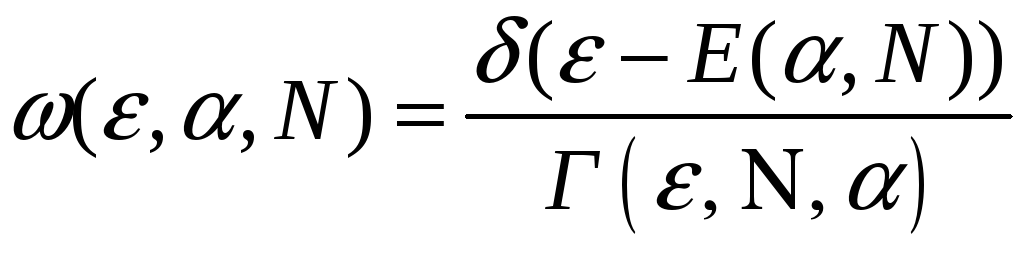– микроканоническое распределение Гиббса.

– энтропия. .

2. Распределение Гиббса.

;

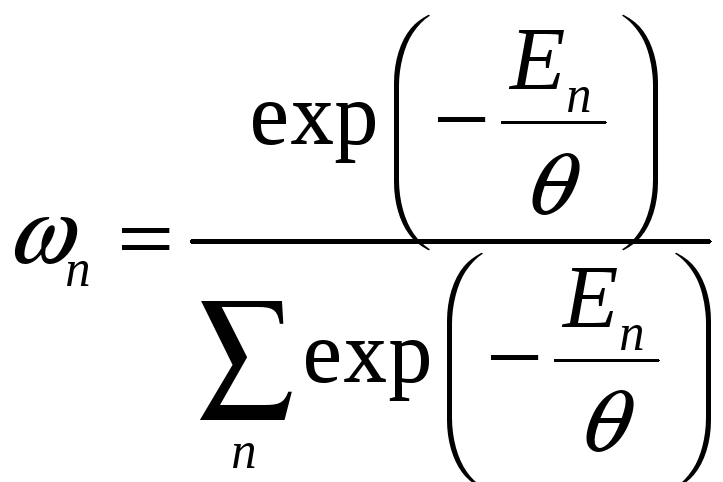– свободная энергия.

3. Большое каноническое распределение (для ):

.

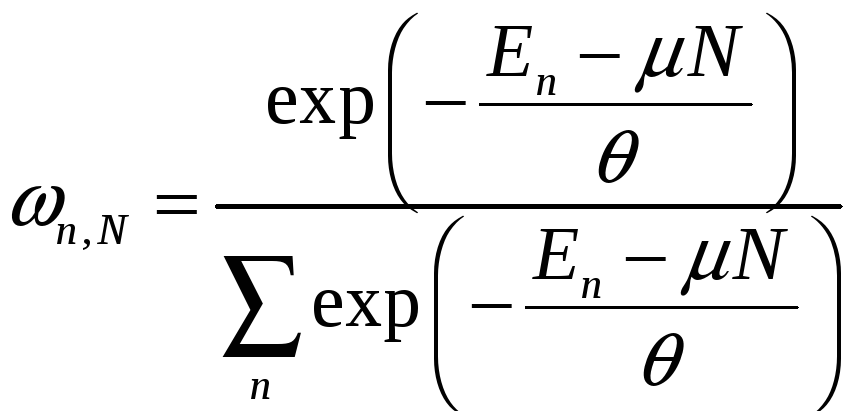8. Идеальный Бозе- и Ферми-газы. Равновесное излучение.

Ферми – Газ

– число частиц с энергией .

Плотность вероятности: ,

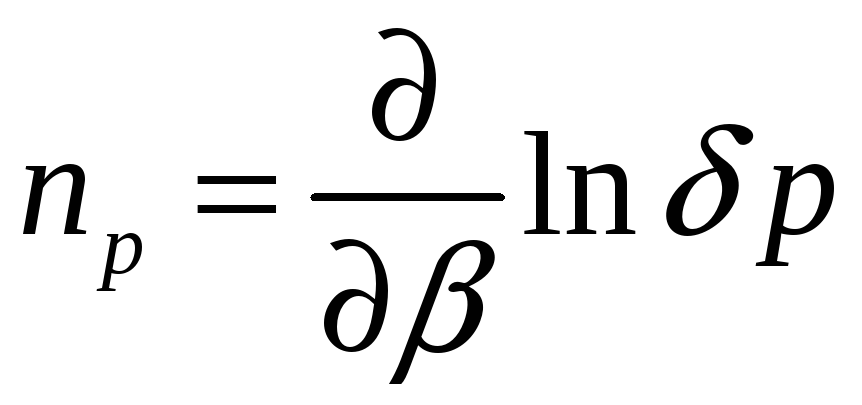где ,

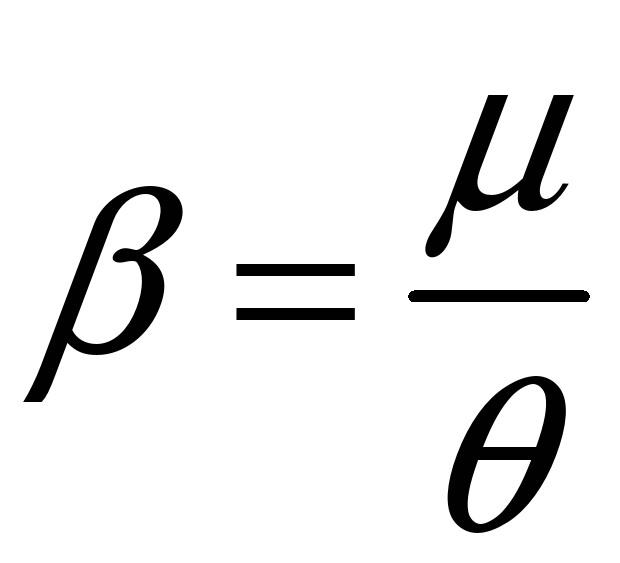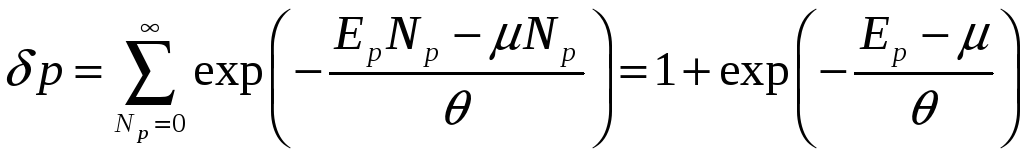
(для первого слагаемого , для второго – ).

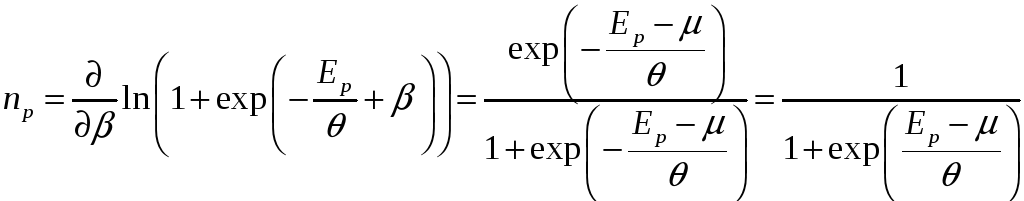
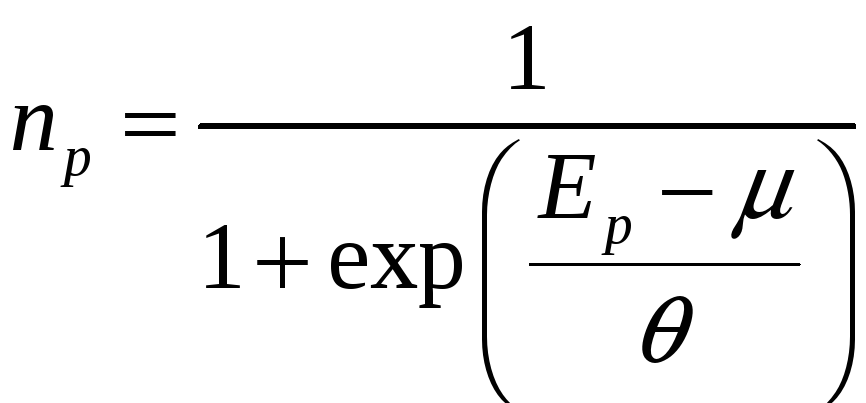
Бозе – газ.

.

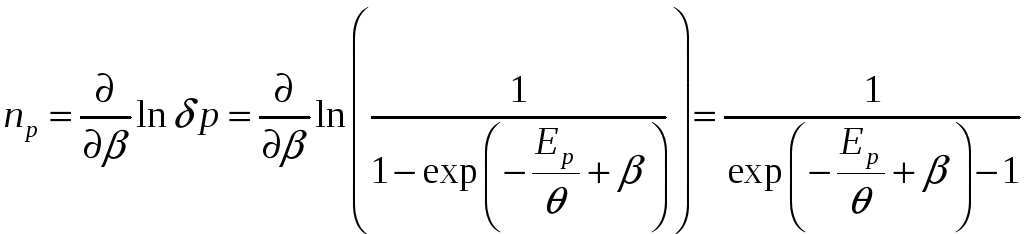Равновесное излучение.

, , где

,

, ;

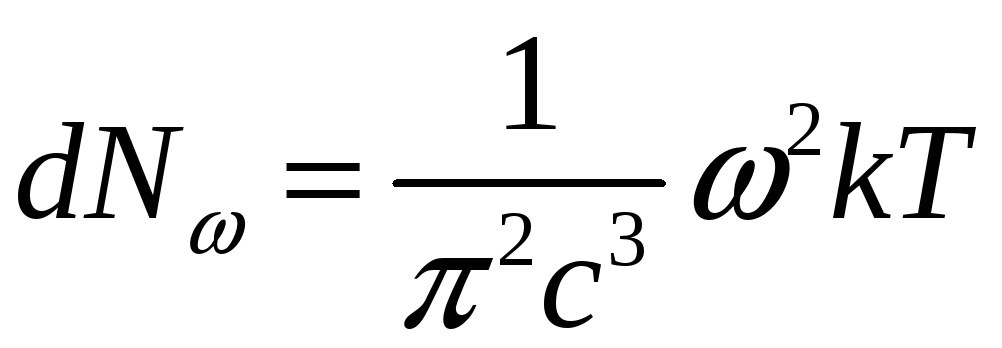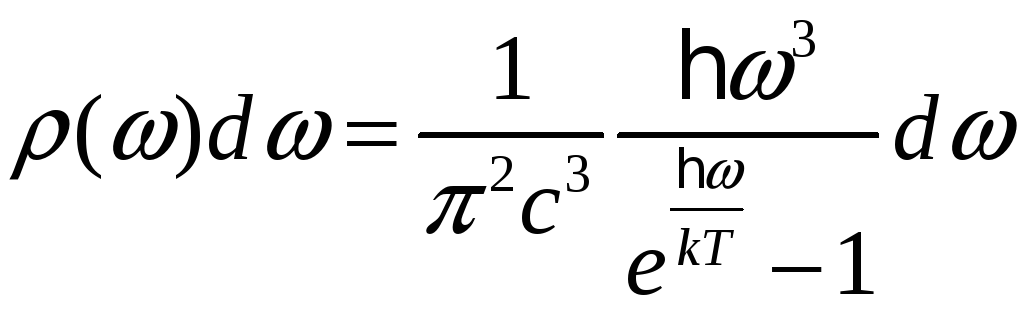
9. Теплоемкость твердых тел. Модели Дебая и Эйнштейна.

Теплоемкость твердого тела.

Теплоемкость при постоянном объеме определяется соотношением: 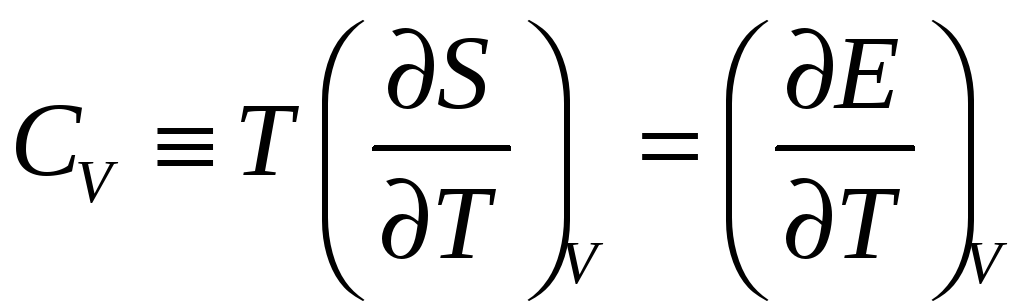, где – энтропия, – внутренняя энергия, – абсолютная температура.

1. При комнатных температурах значение теплоемкости почти всех твердых тел близки к .

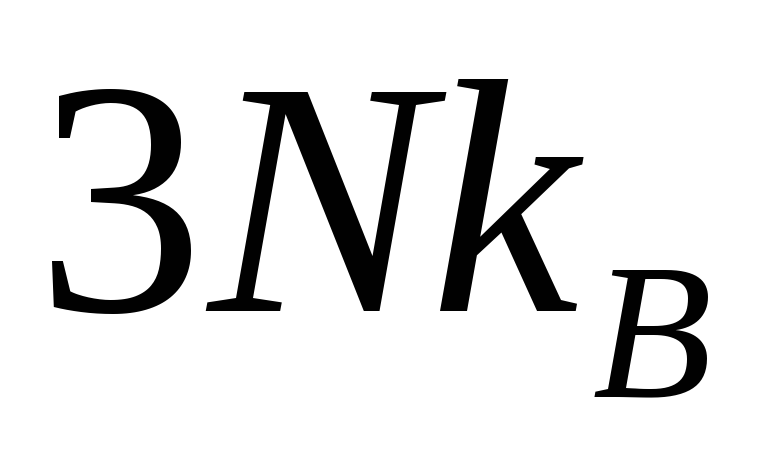2. При низких температурах теплоемкость заметно уменьшается, и в области абсолютного нуля температур приближается к нулю по закону для диэлектриков и по закону для металлов; если металл переходит в сверхпроводящие состояние, то закон уменьшения теплоемкости более резкий, чем .

Модель Эйнштейна.

Средняя энергия линейного осциллятора с частотой равна . Энергия системы из одномерных осцилляторов, имеющих одну и туже резонансную частоту , равна просто сумме энергий осцилляторов:

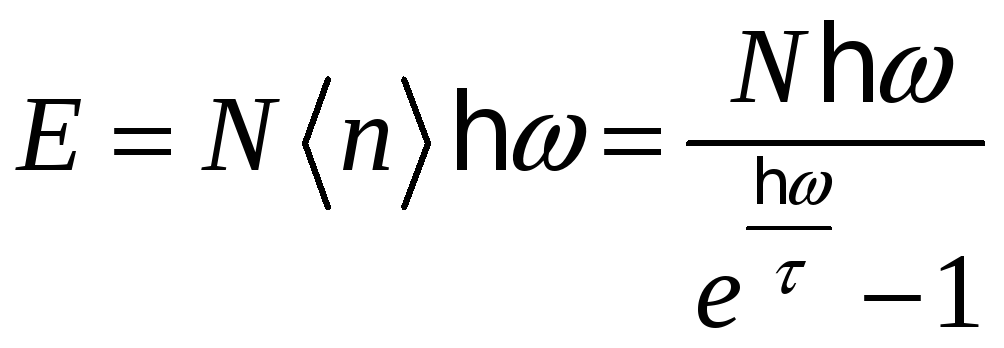
Тогда теплоемкость этой системы осцилляторов:

Таков, по эйнштейновской модели, вклад, который дают осцилляторов одинаковой частоты в теплоемкость твердого тела. Если вместо взять (поскольку каждый из атомов имеет три степени свободы), и предельный случай приведенной выше формулы, отвечающий высоким температурам, то мы получим

.

Модель Дебая. 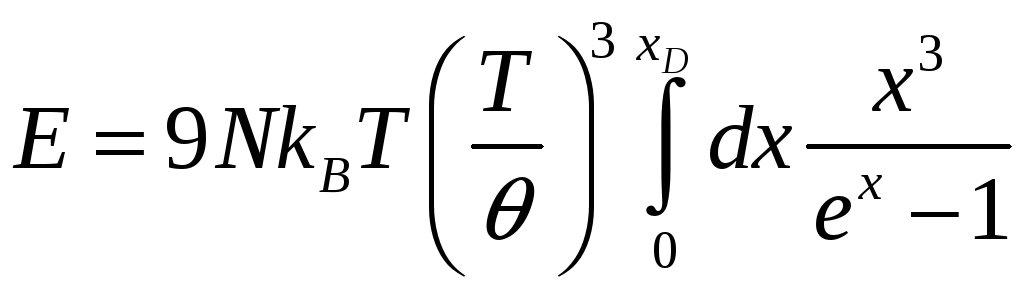, где 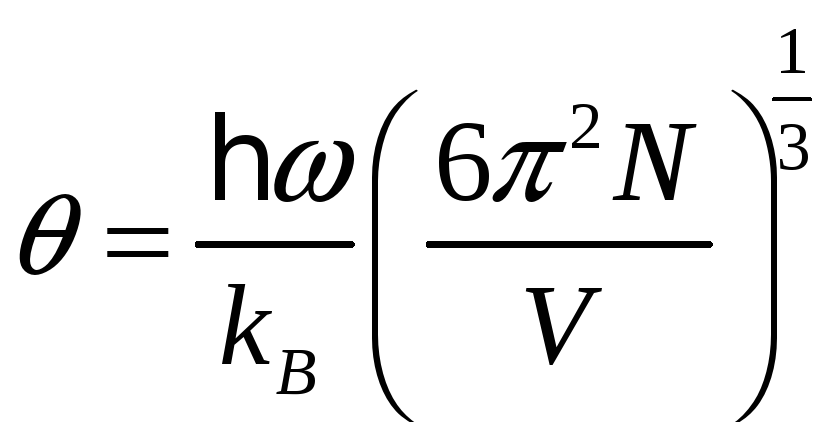– температура Дебая, – число атомов образца,

Тогда теплоемкость этой системы определяется как: .

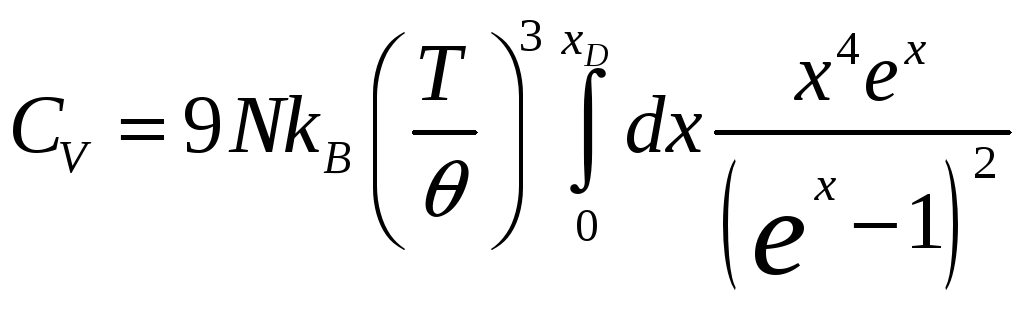При очень низких температурах, т.е. положив верхний придел равным :

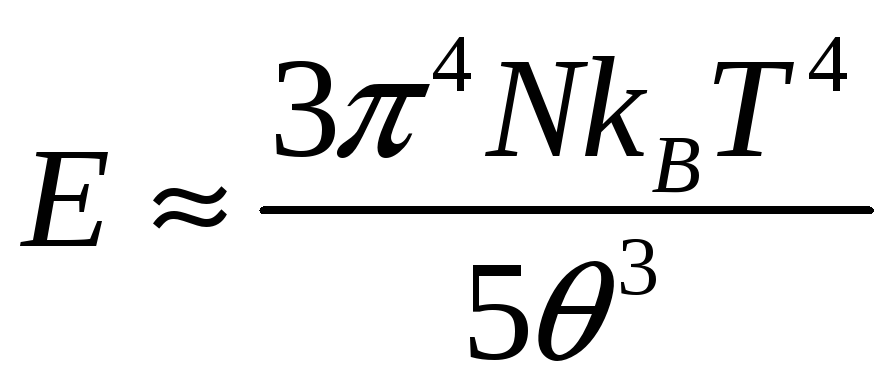при ,

.
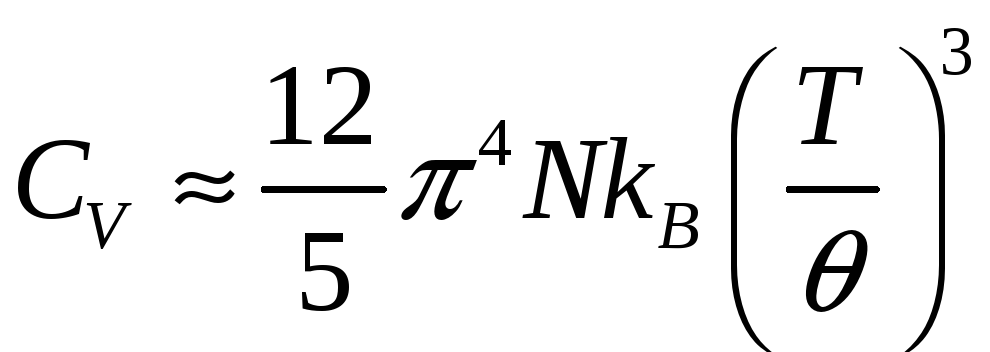