24. Отношения в логике. Умозаключения из суждений с отношениями рефлексивности, симметричности, транзитивности: определения, символическая запись.

25. Умозаключения по логическому квадрату. Запись умозаключений на основе логического квадрата в виде формул. Примеры.

Учитывая отношения между категорическими суждениями А, Е, I, О, которые продемонстрированы схемой логического квадрата, можно строить выводы, основываясь на истинности или ложности исходного суждения.

Выводы строятся по схемам:

Отношения противоречия (А – О; Е - I):

Отношение контрарности (противоположности) (А - Е):

Отношение подпротивности (I - О):

Отношение подчинения (А – I; Е - О):

В качестве примера можно построить вывод на отношения противоположности (A-E) из общеутвердительного суждения (A): «Все жидкости упруги», истинность которого установлена, можно сделать заключение о ложности общеотрицательного суждения (E): «Неверно, что ни одна жидкость не является упругой».

26. Непосредственное умозаключение. Умозаключения превращения, символическая запись, примеры.

К непосредственным умозаключениям относятся следующие виды:

1. превращение;

2. обращение;

3. контрапозиция (противопоставление предикату);

4. умозаключение по логическому квадрату.

Превращение – такое непосредственное умозаключение, в котором устанавливается связь между понятием, являющимся субъектом исходного суждения, и понятием, противоречащим предикату исходного суждения. Например:

.

Исходное суждение – общеутвердительное (А) превращается в общеотрицательное (Е).

Общеотрицательное (Е) превращается в общеутвердительное (А). Например:

.

Частноутвердительное суждение (I) превращается в частноотрицательное (О). Например:

.

Частноотрицательное (О) превращается в частноутвердительное (I). Например:

.

В результате операции превращения меняется качество суждения, но количество остается прежним.

27. Умозаключения обращения (с ограничением и без ограничения), символическая запись, примеры.

К непосредственным умозаключениям относятся следующие виды:

1. превращение;

2. обращение;

3. контрапозиция (противопоставление предикату);

4. умозаключение по логическому квадрату.

Обращение – такое непосредственное умозаключение, в результате которого субъект исходного суждения становится предикатом, а предикат – субъектом заключения. Например:

В зависимости от распределенности терминов исходного суждения различают два вида обращения:

1. простое (чистое) обращение;

2. нечистое обращение.

Простое (чистое) обращение имеет место в том случае, если оба термина (субъект и предикат) исходного суждения являются распределенными или оба являются нераспределенными. Например:

.

При чистом обращении А обращается в А:

Е обращается в Е:

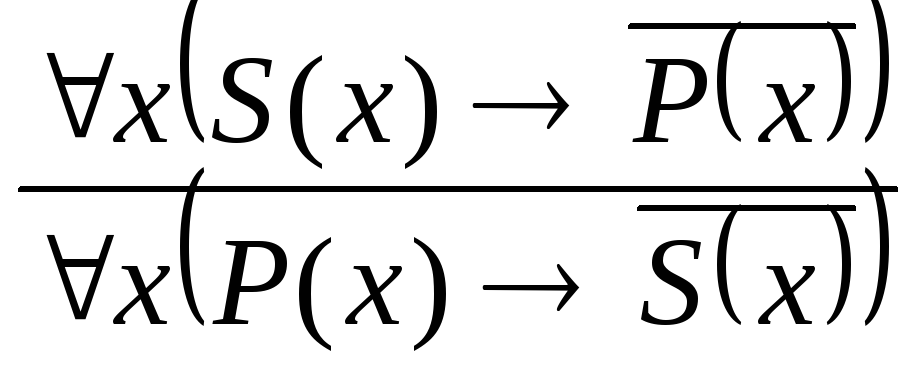
Например:

.

I обращается в I:

Например:

.

Частноотрицательные суждения не обращаются с необходимостью.

Нечистое обращение представлено двумя вариантами:

1. обращение с ограничением;

2. обращение с приращением.

Обращение с ограничением имеет место при переходе от общеутвердительных суждений (А) к частноутвердительным (I):

Например:

Обращение с приращением имеет место в случае выделяющих суждений и связано с переходом от частных суждений к общим:

Например: