Операторы ограничения и прерывания цикла

Данные операторы применяются внутри операторов цикла с параметром или условием. Операторы имеют вид:

Continue; - ограничение цикла,

Break; - прерывание цикла.

Операторы Continue и Break позволяют производить действия не для всех операторов внутри цикла. Действие оператора Continue заключается в передаче управления на начало цикла, при этом контролируется условие выхода из цикла. Действие оператора Break заключается в передаче управления оператору, следующему за последним оператором цикла, при этом не контролируется условие выхода из цикла. Во вложенных циклах операторы Continue и Break действуют только на цикл в котором они записаны. Приведем пример использования операторов для блокировки несанкционированного доступа в программу.

For i := 1 to 3 do

begin

Write( 'Введите ПАРОЛЬ:' ); Readln(S); {S и Parol - переменные одного типа}

If S = Parol Then Break { прерывание цикла }

else If i <> 3 Then Continue; { ограничение цикла }

Writeln( 'Доступ к программе ЗАПРЕЩЕН' );

Writeln( 'Нажмите Enter' );

Readln;

Halt { прерывание программы }

end; { продолжение программы }

Примеры

Пример1: На промежутке от 1 до M найти все числа Армстронга. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенных в n-ю степень, равна самому числу. Этапы решения задачи:

1. Математическая модель: xО[1;M], x=

2. Составим блок схему программы:

Распишем составные части блока"Находим все числа Армстронга на заданном промежутке и печатаем их"

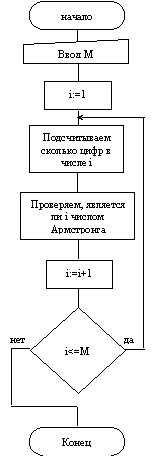
Опишем блок "Подсчитываем сколько цифр в числе i"

Опишем блок "Проверяем, является ли i числом Армстронга"

Дальнейшая детализация не требуется, запишем блок-схему целиком:

Дальнейшей детализации не требуется, переведем программу на язык Паскаль.

PROGRAM Primer_1;

var i,k,s,p,n: Integer;

BEGIN

Write('Введите M ');

Readln(m);

For i:=1 to M do

begin

s:=0; k:=i; n:=0;

While k<>0 do

begin k:=k DIV 10; n:=n+1 end;

k:=i;

While k<>0 do

begin p:=k MOD 10; k:=k DIV 10;

If p<>0 then s:=Trunc (s+Exp(n*Ln(p)))

end;

If s=f then WriteLn (f)

end;

END.

Контрольные вопросы

1. Как записывается и как работает оператор FOR?

2. Для организации каких циклов применим оператор FOR?

3. В чем отличие оператора WHILE от оператора REPEAT?

4. Как программируются циклические алгоритмы с явно заданным числом повторений цикла?

5. Как программируются циклические алгоритмы с заранее неизвестным числом повторений цикла?

6. Напишите оператор цикла, который не выполняется ни разу.

7. Напишите оператор цикла, который выполняется неограниченное число раз.

8. Замените оператор "Repeat A Until B" равносильным фрагментом программы с оператором While.

Задачи

1. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.

2. Найти все трехзначные числа, сумма цифр которых равна данному целому числу.

3. Найти все трехзначные числа, средняя цифра которых равна сумме первой и третьей цифр.

4. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры.

5. Найти все двузначные числа, сумма квадратов цифр которых делится на 17.

6. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр.

7. Найти двузначное число, обладающее тем свойством, что куб суммы его цифр равен квадрату самого числа.

8. Найти двузначное число, равное утроенному произведению его цифр.

9. В каких двузначных числах удвоенная сумма цифр равна их произведению?

10. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи. Вычисление выражений: Дано натуральное n. Вычислить:

11. ;

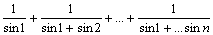12. ; Дано действительное число х, натуральное число n. Вычислить:

13. x ( x - n )( x - 2 n )( x - 3 n )…( x - n2 );

14. ;

15. ; Дано натуральное n. Вычиcлить:

16. ;

17. ;

Вычислить приближенно значение бесконечной суммы (справа от каждой суммы дается ее точное значение, с которым можно сравнить полученный ответ):

18. = ;

19. = ;

20. = ; Нужное приближение считается полученным, если вычислена сумма нескольких первых слагаемых, и очередное слагаемое оказалось по модулю меньше данного положительного числа e.

21. Даны два целых числа A и B (A < B). Вывести все целые числа, расположенные между данными числами (не включая сами эти числа), в порядке их возрастания, а также количество N этих чисел.

22. Даны два целых числа A и B (A < B). Вывести все целые числа, расположенные между данными числами (включая сами эти числа), в порядке их убывания, а также количество N этих чисел.

23. Дано вещественное число A и целое число N (> 0). Вывести A в степени N: AN = A·A·...·A (числа A перемножаются N раз).

24. Дано вещественное число A и целое число N (> 0). Вывести все целые степени числа A от 1 до N.

25. Дано вещественное число A и целое число N (> 0). Вывести 1 + A + A2 + A3 + ... + AN.

26. Дано вещественное число A и целое число N (> 0). Вывести 1 - A + A2 - A3 + ... + (-1)NAN.

27. Дано целое число N (> 1). Вывести наименьшее целое K, при котором выполняется неравенство 3K > N, и само значение 3K.

28. Дано целое число N (> 1). Вывести наибольшее целое K, при котором выполняется неравенство 3K < N, и само значение 3K.

29. Дано вещественное число A (> 1). Вывести наименьшее из целых чисел N, для которых сумма 1 + 1/2 + ... + 1/N будет больше A, и саму эту сумму.

30. Дано вещественное число A (> 1). Вывести наибольшее из целых чисел N, для которых сумма 1 + 1/2 + ... + 1/N будет меньше A, и саму эту сумму.

31. Дано целое число N (> 0). Вывести произведение 1·2·...·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

32. Дано целое число N (> 0). Если N - нечетное, то вывести произведение 1·3·...·N; если N - четное, то вывести произведение 2·4·...·N. Чтобы избежать целочисленного переполнения, вычислять это произведение с помощью вещественной переменной и выводить его как вещественное число.

33. Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). Отрезок [A, B] разбит на равные отрезки длины H с концами в N точках вида A, A + H, A + 2H, A + 3H, ..., B. Вывести значение H и набор из N точек, образующий разбиение отрезка [A, B].

34. Дано целое число N (> 2) и две вещественные точки на числовой оси: A, B (A < B). Функция F(X) задана формулой F(X) = 1 - sin(X). Вывести значения функции F в N равноотстоящих точках, образующих разбиение отрезка [A, B]: F(A), F(A + H), F(A + 2H), ..., F(B).

35. Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 2, AN = 2 + 1/AN-1, N = 2, 3, ... Найти первый из номеров K, для которых выполняется условие |AK - AK-1| < D, и вывести этот номер, а также числа AK-1 и AK.

36. Дано число D (> 0). Последовательность чисел AN определяется следующим образом: A1 = 1, A2 = 2, AN = (AN-2+ AN-1)/2, N = 3, 4, ... Найти первый из номеров K, для которых выполняется условие |AK AK-1| < D, и вывести этот номер, а также числа AK-1 и AK.