Контрольные вопросы

1. Для чего нужны в программе процедуры и функции?

2. В чем отличие между процедурой и функцией?

3. Чем отличаются формальные и фактические параметры?

4. Чем отличаются параметры-значения и параметры-переменные?

5. Как объявляются глобальные и локальные переменные? Каково правило видимости этих переменных?

6. Почему при обращении к процедуре, аргумент, передаваемый параметру-переменной, может быть только переменной, а не константой или выражением?

Пример

Пример1. Найти сумму положительных элементов в массиве. Этапы решения задачи:

1. Алгоритм решения довольно прост - в цикле будем "пробегать" массив, сравнивая его ячейки с 0 и суммировать, если они >0.

2. Составим блок-схему программы

Уточним из каких блоков состоит блок"Суммирование положительных ячеек"

Содержание этих блоков простое, поэтому не стоит их уточнять.

3. Напишем программу на языке Паскаль

program example;

type

Tarray = array[1..100] of integer;

Var v: Tarray;

N,i,s:integer;

Procedure vvod_data(var m:Tarray;n:integer);

Var i:integer;

Begin

Writeln('Введите ',n,' чисел через пробел');

For i:= 1 to n do read(m[i]);

End;

Function summ(m:TArray):integer;

Var s:integer;

Begin

S:=0;

For i:= 1 to n do if m[i]>0 then s:= s+m[i];

Summ:=s;

End;

begin

write('Введите размерность массива N= '); readln(n);

vvod_Data(v,n);

s:= summ(v);

writeln('Сумма= ',s);

end.

Задания

1. Описать функции Min2(A,B) и Max2(A,B)2 вещественного типа, находящие минимальное и максимальное из двух вещественных чисел A и B.

2. Описать процедуру Minmax(A,B), записывающую в переменную A минимальное из значений A и B, а в переменную B - максимальное из этих значений.

3. Описать функцию Fact(N) целого типа, вычисляющую значение факториала N! = 1·2·...·N (N > 0 - параметр целого типа). С помощью этой фунции вычислить факториалы 10 данных чисел.

4. Описать процедуру SumDigit(N,S), находящую сумму цифр S целого числа N (N - входной, S - выходной параметр). Используя эту процедуру, найти суммы цифр пяти данных чисел.

5. Описать функцию Polynom(A,N,X) вещественного типа, находящую значение полинома P в вещественной точке X. Полином P задается параметрами N (степень полинома, 0 < N < 8) и A (коэффициенты полинома, вещественный массив размера N+1): P(X) = A[1]·XN + A[2]·XN-1 + ... + A[N]·X + A[N+1]. Используя эту функцию, найти значения заданного полинома в пяти данных точках.

6. Описать функцию Min(A,N) и Max(A,N)2 вещественного типа, находящую минимальный и максимальный элемент массива A, состоящего из N вещественных чисел.

7. Описать функцию NMin(A,N) и NMax(A,N)2 целого типа, находящую номер минимального и максимального2 элемента массива A (массив состоит из N вещественных чисел).

8. Описать процедуру NMinmax(A,N,NMin,NMax), находящую номера минимального и максимального элемента массива A из N вещественных чисел.

9. Описать процедуру Invert(A,N), меняющую порядок следования элементов массива A из N вещественных чисел на противоположный ("инвертирование массива").

10. Описать процедуру Smooth(A,N), заменяющую каждый элемент вещественного массива A размера N на его среднее арифметическое со своими соседями ("сглаживание массива"). С помощью этой процедуры выполнить пятикратное сглаживание данного массива A размера N, выводя на экран результаты каждого сглаживания.

11. Описать функцию SumLine(A,M,N,k) вещественного типа, вычисляющую сумму элементов вещественной матрицы A размера M x N, расположенных в k-й строке (если [k > M]1|[k > N]2, то функция возвращает 0).

12. Описать функцию SumCol(A,M,N,k)2 вещественного типа, вычисляющую сумму элементов вещественной матрицы A размера M x N, расположенных в k-й столбце (если [k > M]1|[k > N]2, то функция возвращает 0).

13. Описать функцию IsIdent(S) целого типа, проверяющую, является ли строка S допустимым идентификатором Паскаля. При утвердительном ответе возвращается 0. Если S является пустой строкой, то возвращается -1, если строка начинается с цифры, то возвращается -2. Если S содержит недопустимые символы, то возвращается номер первого недопустимого символа. Проверить с помощью этой функции пять данных строк.

14. Описать функцию FillStr(S,Len) строкового типа, возвращающую строку длины Len, заполненную повторяющимися копиями строки-шаблона S (последняя копия строки-шаблона может входить в результирующую строку частично).

15. Описать процедуру Trim(S), удаляющую в строке S начальные и конечные пробелы.

16. Описать функцию PosLast(subS,S) целого типа, возвращающую номер позиции, с которой в строке S содержится последнее вхождение подстроки subS. Если в строке S отсутствуют подстроки subS, то функция возвращает 0.

17. Даны действительные числа х1, у1, х2, у2, …,х10, у10. Найти периметр десятиугольника, вершины которого имеют соответственно координаты (х1, у1), (х2, у2), …, (х10, у10). (Определить процедуру вычисления расстояния между двумя точками, заданными своими координатами.)

18. Даны действительные числа a, b, c, d, e - стороны пятиугольника. Найти площадь пятиугольника. (Определить процедуру вычисления площади треугольника по его сторонам.)

19. Даны три символьные матрицы. a) ту матрицу, где есть хотя бы одна гласная - транспонировать; b) в той матрице, на главной диагонали которой все цифры, найти наименьшую и удалить соответствующую строку.

20. Написать программу вычисления P по формуле: где n - заданное натуральное число.

21. Описать функцию Stepen (x,n) от вещественного x и целого n, вычисляющую (посредством умножения) величину xn, и использовать ee для вычисления b=2.7k+(a+1)-5.

22. Даны отрезки a,b,c и d. Для каждой тройки этих отрезков, из которых можно построить треугольник, напечатать площадь данного треугольника. Определить процедуру Plo(x,y,z), печатающую площадь треугольника со сторонами x,y и z, если такой треугольник существует.

23. Пусть процедура Socr(a,b,p,q) от целых параметров (b№0)приводит дробь к несократимому виду Описать данную процедуру и использовать ее для приведения дроби к несократимому виду

24. Даны длины a,b и c сторон некоторого треугольника. Найти медианы треугольника, сторонами которого являются медианы исходного треугольника. Длина медианы, проведенной к стороне a, равна

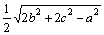
25. Даны координаты вершин двух треугольников. Определить, какой из них имеет большую площадь.

26. Даны координаты вершин треугольника и координаты некоторой точки внутри него. Найти расстояние от данной точки до ближайшей стороны треугольника. (При определении расстояний учесть, что площадь треугольника вычисляется и через три его стороны, и через основание и высоту.).

27. Три прямые на плоскости заданы уравнениями akx+bky=ck, k=1,2,3. Если эти прямые попарно пересекаются и образуют треугольник, тогда найти его площадь.

28. Два натуральных числа называются "дружественными", если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Напечатать все пары "дружественных" чисел, не превосходящих заданного натурального числа.

29. Дано четное число n > 2. Проверить для этого числа гипотезу Гольдбаха. Эта гипотеза (по сегодняшний день не опровергнутая и полностью не доказанная) заключается в том, что каждое четное n, большее двух, представляется в виде суммы двух простых чисел. Воспользоваться функцией распознавания простых чисел.

30. Дано натуральное число n. Выяснить, является ли оно полным квадратом. Определить функцию, позволяющую распознавать полные квадраты.

31. Дан массив A[1..50], элементы которого отличны от нуля. Расположить их в таком порядке, чтобы первыми были все положительные элементы, а затем - все отрицательные, причем порядок следования как положительных, так и отрицательных элементов должен сохраниться (при решении задачи новый массив не заводить!).

32. Преобразовать массив S, "поворачивая" его вокруг центра на 90, 180, 270 градусов против часовой стрелки.

33. Рассматривая массивы X, Y и Z как представление некоторых множеств из объектов типа индекс (X[k]=TRUE, если элемент k принадлежит множеству X, и X[k]=FALSE иначе, и т.п.), реализовать следующую операцию над этими массивами-множествами: переменной t присвоить значение TRUE, если множество X является подмножеством множества Y, и значение FALSE иначе.

34. Элемент двухмерного массива называется локальным минимумом, если он строго меньше всех имеющихся у него соседей. Подсчитать количество локальных минимумов заданной матрицы размером NxN найти максимум среди всех локальных минимумов.

35. Составить функцию для нахождения точного значения суммы натуральных чисел, в десятичной записи которых более 20 знаков. Указание. Исходные данные и ответ представить в виде массивов цифр.

36. Даны две строки символов. Символ будем называть общим, если он встречается и в первой, и во второй строке. Пусть K1 - число вхождений в первую строку общего символа, а K2 - во вторую. Минимальное из чисел K1, K2 будем называть числом общности. Вывести все общие символы с указанием для них числа общности.