Лабораторна робота № 8

Тема: Розрахунок надійності послідовної системи за критерієм міцності при нормальному розподілі навантаження.

Мета роботи: ознайомитися і практично освоїти метод розрахунку на стадії проектування надійності електромеханічних систем.

Загальні відомості

У розрахунках основних деталей машин, крім підшипників кочення, міцність визначають за співвідношенням розрахункових напружень та граничних за критерієм міцності напружень деталі , перевищення яких викличе відмовлення.

Напруження та розглядають як незалежні випадкові величини, розподілені за нормальним законом. Кількісно напруження та задають їх числовими характеристиками: середніми значеннями (математичними очікуваннями) та і середніми квадратичними відхиленнями та або коефіцієнтами варіації та .

Імовірність безвідмовної роботи системи за критерієм міцності , або імовірність неруйнування, визначають як імовірність того, що розрахункові напруження не перевищать граничних , тобто

.

Числове значення імовірності неруйнування визначають за таблицями нормального розподілу в залежності від квантилі

, (8.1)

де – коефіцієнт запасу міцності за середніми напруженнями.

Імовірність безвідмовної роботи послідовної системи з несучою здатністю R при навантаженні F дорівнює добутку імовірностей безвідмовної роботи елементів:

(8.2)

де – імовірність безвідмовної роботи -го елемента системи при його навантаженні , – кількість елементів у системі.

Метод оцінки надійності послідовної системи для випадку нормального розподілу навантаження та несучої здатності полягає в наступному.

1. Задаються двома значеннями фіксованих навантажень і . Навантаження вибирають так, щоб при оцінці надійності системи імовірності її безвідмовної роботи отримувались в межах і . Орієнтовні значення навантажень можна приймати:

(8.3)

2. За формулою (8.2) проводять розрахунок імовірностей безвідмовної роботи системи при цих навантаженнях. Переконуються, що отримані значення та знаходяться в допустимих межах. У противному разі необхідно змінити значення та .

3. За таблицею 1 Додатку знаходять квантілі нормованого нормального розподілу та , що відповідають знайденим імовірностям.

4. Апроксимують закон розподілу несучої здатності системи нормальним розподілом з математичним очікуванням 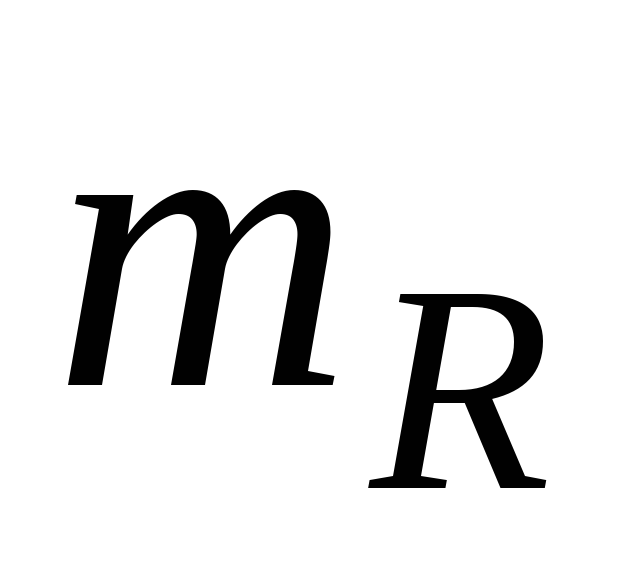і коефіцієнтом варіації .

Квантіль нормального розподілу для визначення імовірності безвідмовної роботи системи за критерієм несучої здатності при фіксованому навантажені дорівнює:

. (8.4)

Для навантажень та квантілі дорівнюватимуть відповідно

; (8.5)

. (8.6)

Запишемо отримані вирази у вигляді системи рівнянь:

(8.7)

Вирішуючи спільно ці рівняння, і враховуючи, що , отримують вирази для математичного очікування та коефіцієнта варіації несучої здатності системи:

; (8.8)

; (8.9)

4. За формулою (8.1) обчислюють квантіль та знаходять відповідну їй імовірність безвідмовної роботи за таблицею 1 Додатку.