2.3.Соотношения, используемые для расчета электрических характеристик антенны

Параметры ферритовых стержней линзы таковы, что связь между ними (взаимодействие) пренебрежимо мала и их можно рассматривать как неэкранированные фазовращатели, а для расчета фазовых распределений и диаграмм направленности использовать соотношения для фазированных антенных решеток [2].

Расчет амплитудно-фазового распределения поля в раскрыве антенны

Используемые соотношения поясняются рисунками 2 и 4.

Распределение амплитуд рассчитывается с учетом структуры поля в возбуждающем волноводе и изменений, вносимых металло-воздушной линзой. Для определения амплитуд поля в областях, примыкающих к ферритовым стержням, следует воспользоваться соотношениями

(1)

,

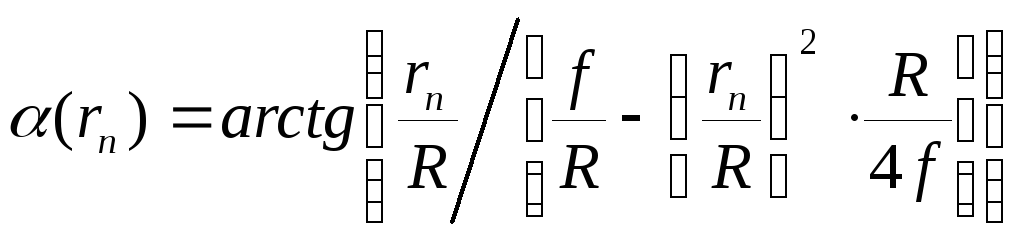где - угол раствора рупора; - фокусное расстояние параболического изгиба; - раскрыв антенны; r_n-координата n-го стержня; r_n=dn; d – период решетки стержней; n-номер стержня при отсчете от центра решетки (n=0,1,2…14).

Распределение фаз (при идеальном фазировании в направлении  ₀):

, (2)

где: - волновое число; - направление главного лепестка диаграммы направленности.

Регулировка фазы осуществляется в пределах от 0 до 2 и соответствующее фазовое распределение определяется соотношением:

, где m=0,1,2 … (3)

Дискретные значения фазы, устанавливаемые с помощью ферритовых элементов линзы:

, (4)

где - целая часть x;  - дискрет регулировки фазы.

С учетом краевых эффектов принимается (r₁₅)=(r₁₄) и А(r₁₅)=А(r₁₄).

Формулы (1) и (2) являются приближенными и не учитывают неравномерности в распределении амплитуд и фаз поля в раскрыве, обусловленные взаимодействием ферритовых элементов.

Расчет диаграммы направленности антенны в плоскости сканирования:

Рассматривая ферритовые стержни управляемой линзы как излучатели с диаграммой направленности вида , воспользуемся соответствующей формулой для ФАР.

Нормированная диаграмма направленности для симметричной ФАР с нечетным числом элементов, размещенных с шагом d, имеет вид:

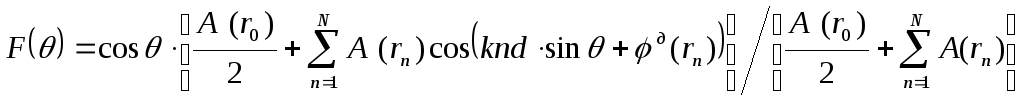. (5)

Расчет коэффициента усиления антенны:

Для расчета используется соотношение

, (6)

где  - коэффициент полезного действия;  - коэффициент, учитывающий дискретность регулировки фазы в элементах линзы; c – коэффициент, зависящий от дисперсии фазовых ошибок; g – коэффициент использования поверхности раскрыва антенны; S – площадь раскрыва антенны.

С учетом того, что распределение амплитуд вдоль раскрыва в плоскости Н близко к косинусоидальному, а в ортогональном направлении - равномерное с фазой, изменяющейся по квадратичному закону, можно принять g0.7 .Остальные величины:

; =0.8; S=LB;  - дискрет регулировки фазы; с=exp(-_ф-_а); _ф,_а – дисперсии фазовых и амплитудных ошибок, значения которых с учетом характеристик используемых фазорегулирующих элементов могут быть приняты равными _ф=_а=0.1.

2.4.Порядок расчета характеристик антенны

1. Рассчитать по формуле (1) значения А_n амплитуд поля в точках раскрыва антенны, лежащих напротив осей ферритовых стержней линзы.

2. Рассчитать для стержней линзы по формуле (2) значения фазовых сдвигов, соответствующие идеальному фазированию антенны при ориентации главного максимума диаграммы в направлениях ₀=0, ₀=₁ и ₂ (₁ и ₂ – задаются преподавателем). Результаты расчетов занести в таблицу 1.

3. Рассчитать по формуле (4) значения фазовых сдвигов, соответствующие указанным углам ₀ при регулировке фазы с дискретом =45. Результаты занести в таблицу 2 в виде схемы положения тумблеров на пульте фазирования.

4. Выполнить расчеты, указанные в п.3, для случая фазирования с дискретом =90.

5. По формуле (6) рассчитать значения G, соответствующие ₀=₁ и ₂ и дискрету фазирования =45.

6. Рассчитать по формуле (5) диаграммы направленности антенны, соответствующие ₀=0, ₀=₁, и ₀=₂ при идеальном фазировании, фазировании с дискретом 45.

7. Расчеты по п.5 и 6 выполнить для фазирования с дискретом =90. Результаты расчетов отобразить графически в прямоугольной системе координат.

8. Ориентировочно определить предельный угол отклонения луча.

Примечание:

Студенты 3-го курса выполняют расчеты по пунктам 1,2,3,5,6.