Вопрос 21. Вероятностное описание случайных погрешностей. Плотность распределения и ее свойства.

Более наглядным является описание свойств результатов измерений и случайной погрешности с помощью дифференциальной функции распределения, иначе называемая плотностью распределения величины Х. f(x)=dF(x) / dx=

Плотность распределения всегда неотрицательна, и подчиняется условию нормирования в виде

Учитывая взаимосвязь между F(x) и f(x):

легко показать, что вероятность попадания случайной величины в интервал от Х₁ до Х₂ равна Р (Х₁ <X <X₂) =

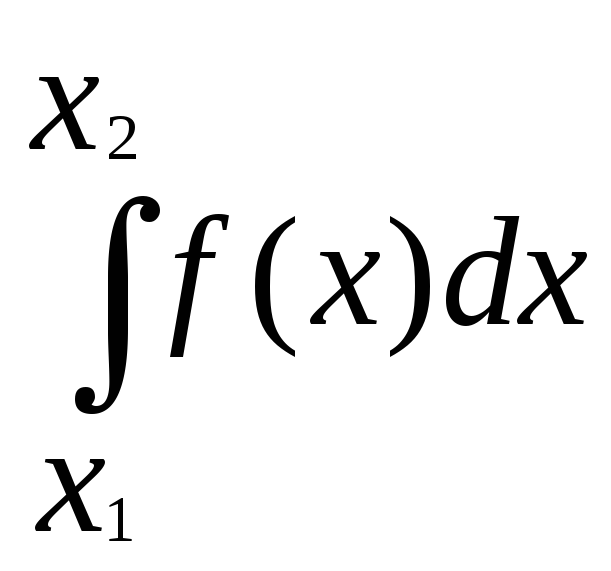
Отсюда видно, что условие нормирования означает, что вероятность попадания величины Х в интервал от - до + = 1. Т.е. представляет достоверное событие.

График плотности распределения имеет вид

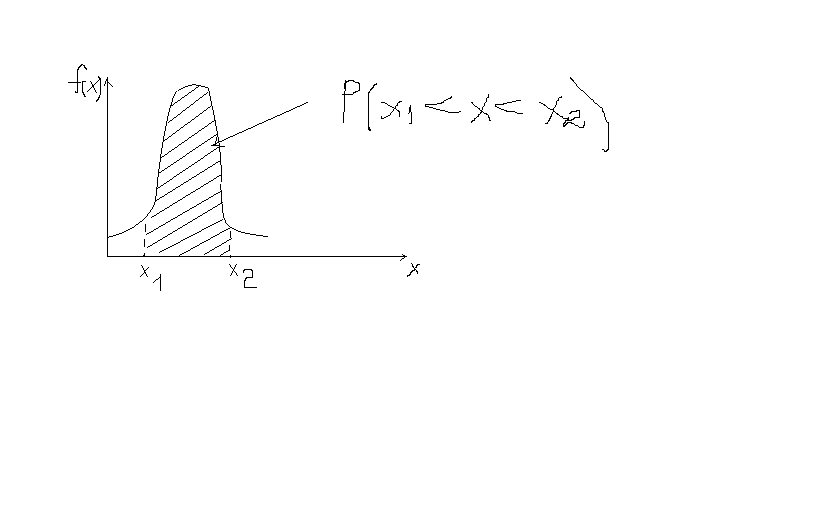
22. Закон распределения суммарной погрешности. Центральная предельная теорема.

Результирующая погрешность часто складывается из ряда составляющих с различными плотностями распределения. В связи с этим возникает задача определения закона распределения суммарной погрешности. Для суммы независимых непрерывных СВ Х₁ и Х_{2 с} с плотностями f₁(X₁) и f₂(X₂). Он (закон) называется композицией и выражается интегралом:

.

Большинство встречающихся на практике погрешностей измерений могут быть представлены как сумма большого числа сравнительно малых слагаемых, каждая из которых вызвана действием отдельной причины, независящей от остальных. Каким бы законам распределения не были подчинены отдельные составляющие погрешности, особенности этих распределений теряются и сумма оказывается подчиненной закону, близкому к нормальному. Это утверждение получило название- центральная предельная теорема теории вероятности. Основное ограничение, налагаемое на суммируемую составляющую, состоит в том, чтобы каждая из них играла в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из составляющих погрешностей окажется по своему влиянию резко превалирующей над всеми другими, то закон ее распределения определит в основных чертах закон распределения суммы.

23. Числовые характеристики случайной величины: мат.Ожидание.

Среди числовых характеристик случайной величины прежде всего отличают те, которые определяют положение случайной величины на числовой оси. Тоесть указывают ориентировочные значения около которого группируются все возможные значения случайной величины.

Характеристикой положения является мат. ожидание:

Пусть имеется дискретная случайная величина Х, ее значения Х₁, Х₂,…,Х_n с вероятностью р₁,р₂,…,р_n.

Для характеристики положения такой СВ на оси абсцисс с учетом того, что ее значения имеют разные вероятности воспользуемся средним взвешиванием.

Рассчитать среднее взвешивание можно из выражения

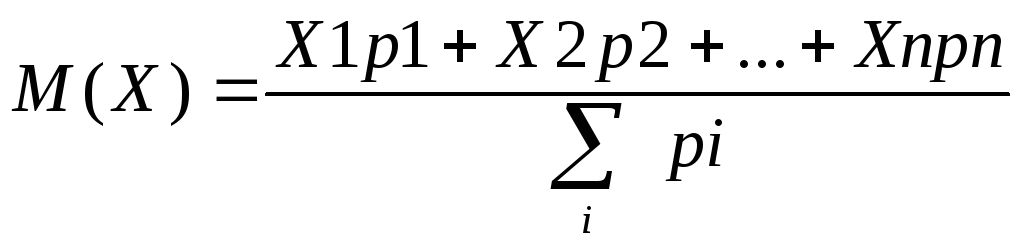(1)

Это среднее взвешивание значений и называется мат. ожиданием СВ.

Мат. ожидание связанное со средним арифметическим. При большом числе опытов среднее арифметическое значение СВ приближается к ее мат. ожиданию. Сред. арифм. Является статистической оценкой мат. ожидания. Если при изучении дискретной СВ Х производят N независимых опытов при чем х₁ появилось m₁ раз и т.д. х_i появилось m_i раз, то среднее арифм. Значение Х определяется по формуле.

Где pi*- статистическая оценка вероятности или частоты.

Среднее арифметическое значений СВ равно сумме произведения всех возможных значений случайной величины на частоты этих значений.

При увеличении кол-ва опытов частоты р* будут приближаться к соответствующей вероятности р., а среднее арифм. m* к мат ожиданию m.

Формула (1) соответств. дискретной СВ для непрерывной СВ

24. Числовые характеристики случайной величины: мода, медиана.

Модой дискретной СВ называется ее наиболее вероятное значение.

Для непрерывной величины модой является то значение в котором плотность вероятность максимальная

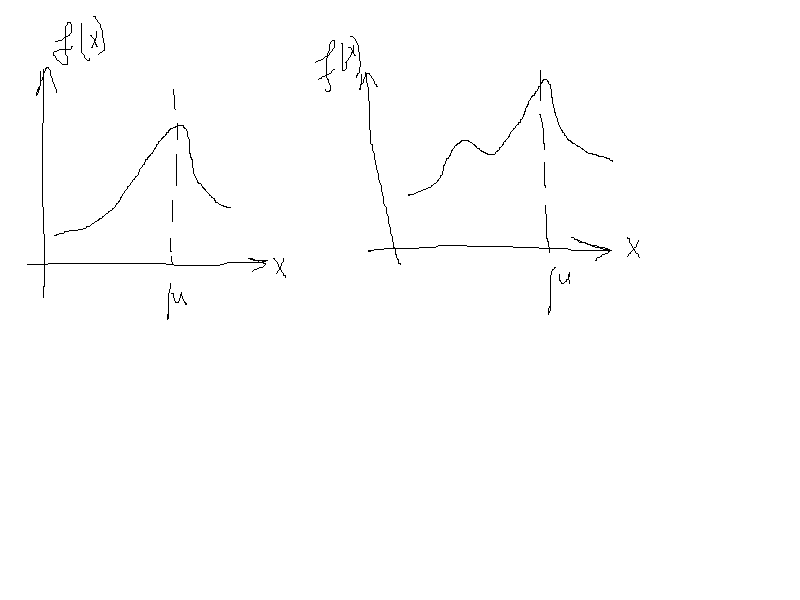
Если кривая распределения имеет более 1 максимального распределения, называется полимодальным.

Иногда встречается распределение обладающее на максимумом а минимумом и называется антимодальное распределение.

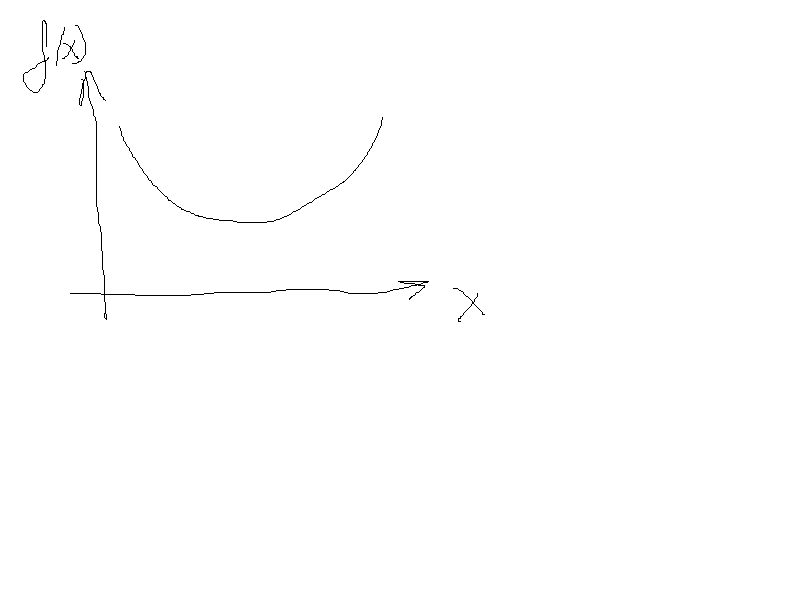
В общем случаи мода и мат. ожидание СВ не совпадает. В частном случаи для симметричного распределения мода совпадает с мат. ожидание и центром симметрии распределения.

Медиана СВ Х – такое значение для которого одинаково вероятно окажется ли СВ больше или меньше медианы.

Геометрически медиана – это абсцисса точки, в которой площадь ограниченная кривой распределения делится напополам.

В случаи симметрии модальное распределение медианы совпадает с мат. ожиданием и модой.