
- •Вопрос 1. Предмет изучения и задачи метрологии.
- •Вопрос 2. Роль экологического обеспечения экологического контроля.
- •3.Этапы формирования метрологии как науки.
- •5. Виды измерения по способу получения и характеру изменения информации. Общая характеристика.
- •6. Виды измерений по количеству, качеству информации, отношению к основным единицам и метрологическому назначению. Общая характеристика.
- •7. Методы измерений. Их классификация и общая характеристика.
- •8. Истинное и действительное значения измеряемой величины. Понятие погрешности измерения.
- •9. Причины, вызывающие погрешность в результатах измерений.
- •10. Классификация погрешностей.
- •11. Виды погрешностей по причине возникновения и форме представления. Их общая характеристика.
- •12. Виды погрешностей по характеру проявления в результатах измерений, условиям возникновения и зависимости от значения измеряемой величины. Общая характеристика.
- •13.Правильность измерений.Способы исключения систематических погрешностей из результата измерений
- •14.Методы устранения постоянной систематической погрешности
- •15. Методы обнаружения и устранения переменных систематических погрешностей из результатов измерений (анализ знаков, графический метод, метод симметричных наблюдений).
- •16. Критерий Аббе.
- •17. Критерий Фишера
- •18. Критерий Вилкоксона
- •19. Исключение систематических погрешностей путем введения поправок.
- •20)Вероятность описания случайной погрешности. Функции распределения её и свойства.
- •Вопрос 21. Вероятностное описание случайных погрешностей. Плотность распределения и ее свойства.
- •22. Закон распределения суммарной погрешности. Центральная предельная теорема.
- •23. Числовые характеристики случайной величины: мат.Ожидание.
16. Критерий Аббе.
Способ последовательных разновидностей состоит в следующем, дисперсию результатов наблюдений можно оценить 2-мя путями:
-
обычным.
2) последовательных разностей. .
Если в процессе измерения происходило смещение центра группирования результатов измерений, т.е. имело место переменная систематическая погрешность, то дает преувеличенную оценку дисперсии результата измерений. В тоже время изменение центра группирования мало сказывается на значении последовательных разностей, поэтому смещения почти не отразятся на значении . Отношение является критерием для обнаружения систематических смещений центров группирования результатов измерений. Для проверки гипотезы о постоянстве центра группирования задаются доверительной вероятностью Р; определяют уровень значимости q=1-P или зная число n по таблице определяют критическое значение критерия Vq.
Если расчетное Vзначение критерия Аббе меньше Vq – критического, то гипотеза о постоянстве центра группирования результатов наблюдений отклоняются, т.е. обнаруживается переменная систематическая погрешность результатов измерений.
17. Критерий Фишера
Дисперсионный анализ (критерий Фишера) состоит в следующем: проводят многократные измерения, состоящие из S серий, каждая из которых соответствует определённому, пусть неизвестному, но различному в каждой серии значению влияющего фактора. В каждой серии n-измерений, а N=S*n – общее кол-во опытов. Если установлено что рез-ты в сериях распределены нормально можно установить имеется ли систематическое расхождение между результатами отдельных серий. Считается, что рассеяние результатов наблюдения в пределах каждой серии характеризует только случайные погрешности измерений и оцениваются величиной внутрисерийной дисперсии
![]() ,
,
Где
![]()
![]() – результат i-го
измерения в j-
той серии. Рассеяние Xj
различных серий обусловлено не только
случайными погрешностями измерений,
но и систематическими различиями между
результатми наблюдения с группированными
по сериям следовательно межсерийная
дисперсия.
– результат i-го
измерения в j-
той серии. Рассеяние Xj
различных серий обусловлено не только
случайными погрешностями измерений,
но и систематическими различиями между
результатми наблюдения с группированными
по сериям следовательно межсерийная
дисперсия.
![]()
Где
![]()
![]() выражает
силу действия фактора, вызывающие
систематические различия между сериями.
Таким образом величина
выражает
силу действия фактора, вызывающие
систематические различия между сериями.
Таким образом величина
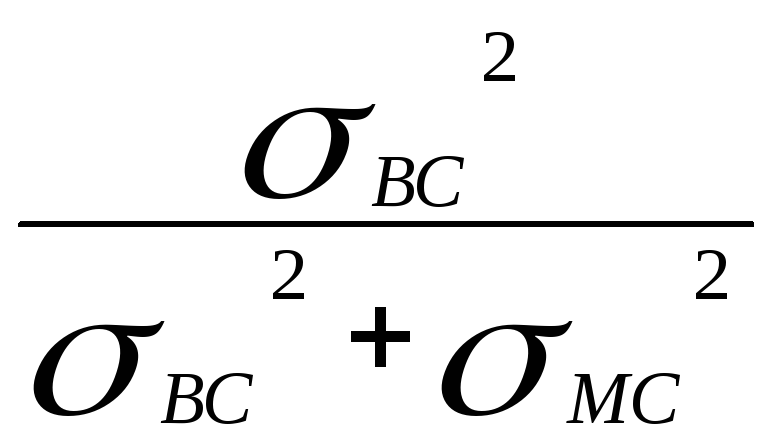 характеризует волю дисперсии
обусловленную наличием случайных
погрешностей измерения, а величина
характеризует волю дисперсии
обусловленную наличием случайных
погрешностей измерения, а величина
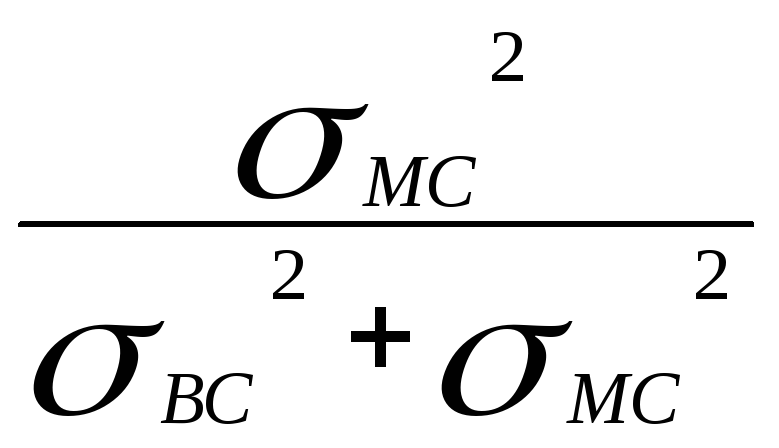 долю дисперсии, обусловленную
межсерийными различиями результатов
наблюдения. Первую из них называют
коэффициентом ошибки, вторую – показателем
дифференциации. Чем больше отношение
показателя дифференциации к коэффициенту
ошибки, тем сильнее действие фактора
по которому группировались серии и тем
больше систематическое различие между
ними. Критерии оценки наличие
систематических погрешностей в данном
случае яв-ся дисперсионный критерий
Фишера
долю дисперсии, обусловленную
межсерийными различиями результатов
наблюдения. Первую из них называют
коэффициентом ошибки, вторую – показателем
дифференциации. Чем больше отношение
показателя дифференциации к коэффициенту
ошибки, тем сильнее действие фактора
по которому группировались серии и тем
больше систематическое различие между
ними. Критерии оценки наличие
систематических погрешностей в данном
случае яв-ся дисперсионный критерий
Фишера
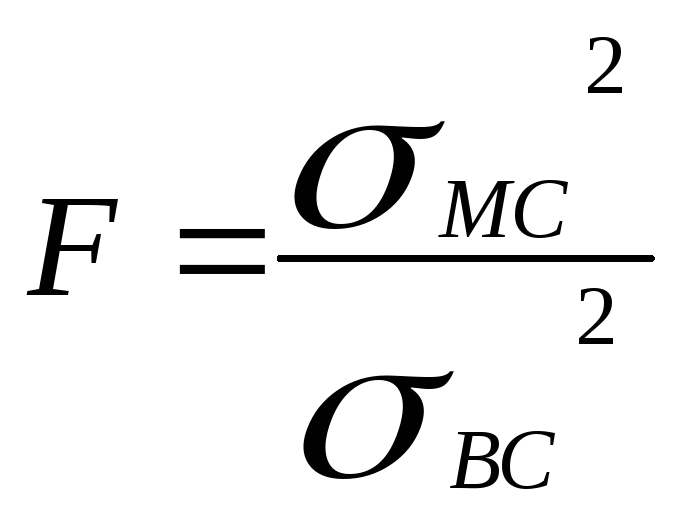
Критические значения этого критерия Fq для различных уравнений значимости q чмсла измерений N и числа серий S приведены в таблице. Если расчетное значение F критерия Фишера больше Fq то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность вызванная тем фактором по которому группировались результаты наблюдения.
