ms_prac

ОПИСОВА СТАТИСТИКА

Основним методом наукових досліджень є експеримент з досліджуваним об'єктом, явищем або процесом. Під експериментом розуміють наукову постановку дослідів і спостереження за поведінкою досліджуваного явища в строго врахованих умовах.

Експериментальні дані формуються шляхом пасивного спостереження або за допомогою активного експерименту. При пасивному спостереженні інформація отримують шляхом реєстрації необхідних відомостей за умови нормального функціонування об'єкта.

В активному експерименті здійснюється цілеспрямована дія на об'єкт за заздалегідь складеною схемою – планом експерименту. Активний експеримент дозволяє суттєво розширити область дослідження, з більшою точністю розкрити закономірності функціонування, скоротити потреби в ресурсах на проведення дослідження.

Проведення будь-якого експерименту супроводжується деякими спрощеннями або допущеннями. Досить часто мають місце випадкові помилки спостережень, які повністю виключити практично неможливо. Тому збір і обробку статистичних даних необхідно здійснювати із застосуванням строгих методів математичної статистики. Метою математичної обробки сукупності отриманих експериментальних даних є:

по-перше, отримання узагальнюючих кількісних та якісних показників, які характеризують досліджуваний обʼєкт, явище або процес;

по-друге, побудова корисної аналітичної моделі досліджуваного об'єкта для виявлення його властивостей і прогнозування його поведінки.

Однак не завжди отримана аналітична модель може бути використана на практиці. Лише за умови дотримання подібності (схожості) математичного опису моделі і об'єкта, модель можна вважати адекватною реальній ситуації, а результати дослідження властивостей моделі можна переносити на об'єкт.

Коректність математичної моделі і можливість її застосування на практиці залежать від того, як спланований експеримент. При дослідженні залежностей мають бути враховані всі значущі фактори та коректно виконана інтерпретація отриманих результатів.

Під плануванням експерименту розуміють оптимальне управління експериментом, коли визначається число і умови проведення дослідів, необхідних і достатніх для вирішення поставленого завдання з необхідною точністю. Початок теорії планування експериментів поклали праці P. Фішера (1935), де він довів, що раціональне планування експериментів дає такий же суттєвий виграш в точності оцінок побудованих залежностей, як і коректна з точки зору математичної статистики обробка результатів вимірювань.

Розвиток інформаційних технологій і можливостей комп'ютерів обробляти великі обсяги інформації зробило доступними для широкого користувача найсучасніші методи статистичного аналізу. На сьогоднішній день існують різні програмні пакети, що реалізують такі можливості.

Вивчаючи той чи інший обʼєкт, явище, процес, в більшості випадків, досліджують якусь певну сукупність, значень деякого показника, який певною мірою характеризує предмет дослідження. Таку сукупність називають генеральною сукупністю. Генеральна сукупність – це множина елементів, об'єднаних загальною характеристикою, що вказує на їхню приналежність до певної системи. Теоретично вважається, що обсяг генеральної сукупності не обмежений. Практично ж обсяг генеральної сукупності завжди обмежений і може бути різним залежно від предмета спостереження і поставленого завдання.

Вибіркою або вибірковою сукупністю називається будь-яка підгрупа елементів, виділена з генеральної сукупності. Обсяг вибірки, звичайно позначається буквою n , може бути будь-яким, але не меншим, ніж два елементи.

До вибірки застосовують низку обов'язкових вимог, визначених, перш за все, цілями і завданнями дослідження. Планування експерименту має включати в себе облік як обсягу вибірки, так і властивих їй особливостей. Так, в багатьох дослідженнях важливою є вимога однорідності

1

вибірки. Ця вимога означає, що не можна включати в одну вибірку різні елементи (елементи як значення різних показників), а лише ті, які характеризують один конкретний показник.

Другою, не менш важливою вимогою якомога більша повнота відображення характеристик досліджуваної генеральної сукупності. Дана властивість вибірки називається репрезентативністю. Репрезентативна вибірка – це вибірка, в якій всі основні ознаки генеральної сукупності відображені приблизно в тій же пропорції і з тією ж частотою, з якою дана ознака виступає в даній генеральної сукупності. Якщо вибірка є репрезентативною, тоді висновки, зроблені на її основі, можна з великою часткою впевненості вважати застосовними до всієї генеральної сукупності.

З точки зору статистики репрезентативність вибірки означає, що представлений вибіркою розподіл значень досліджуваної ознаки відповідає (очевидно, з певною часткою похибки) їх розподілу в генеральній сукупності. Найбільш поширеним методом формування вибірки є відбір елементів з генеральної сукупності. В цьому випадку вибірка складається з елементів, відібраних таким чином, щоб кожен елемент цієї сукупності мав би рівну ймовірність потрапити до вибірки. Отримана таким чином вибірка називається простою випадковою вибіркою. Отримати просту випадкову вибірку можна шляхом звичайного жеребкування (за аналогією з лотереєю) або за допомогою спеціальних таблиць випадкових чисел.

Не менш важливим є визначення обсягу вибірки. Підкреслимо, що він залежить насамперед від завдань дослідження. Очевидно, що більший обсяг вибірки, дозволяє отримати більш надійні результати. Крім того, обсяг вибірки залежить від тих статистичних методів, які передбачається використовувати. Одні методи вимагають великої кількості елементів у вибірці, інші можуть застосовуватися при відносно невеликій їх кількості.

Модель даних у вибірці (дати назви понять)

З основ теорії ймовірності відомо, що кожна випадкова величина повністю визначається своєю функцією розподілу F x Pr X x , X x1 , x2 , , xN , де

Векспериментальних дослідженнях отримані дані мають суттєву випадкову складову, яка відображає вплив різних чинників, отже експериментальні дані практично завжди мають в собі елемент випадковості. Це означає, що розподіл варіант у вибірці відповідає певному закону розподілу випадкових величин. Однак, безпосередньо вказати до якого розподілу належать дані, тобто одному з відомих теоретичних розподілів чи їх суміші практично неможливо. Тим більше, що побудувати емпіричну функцію яка б відповідала конкретному теоретичному розподілу, навіть

втому випадку, коли для досліджуваного об’єкта теоретично обґрунтовано конкретний вид розподілу, задача є досить складною. З другого боку, широко використовуване в теоретичних підходах поняття генеральної сукупності втрачає сенс, якщо характер об’єкта, а отже і даних, є таким як зафіксовано в експериментах, проведених в конкретний відрізок часу, тобто тільки ці дані, отримані визначеними методами і засобами, і тільки вони, найкраще описують даний об’єкт.

Вбагатьох випадках встановлення закону розподілу, як моделі випадкових величин не є метою дослідження, а важливими є лише конкретні кількісні величини, що характеризують отримані дані. Зауважимо, що експериментальні дані, отримані чи безпосередньо вимірюванням, чи в результаті збору в інформативних джерелах, характеризують об’єкт вивчення саме в межах розмаху їх значень в певний період часу і за певних умов. Тому, їх не можна розглядати як просто «фрагмент» деякої генеральної сукупності, оскільки вони є реальною реакцією на дану ситуацію, а їх кількість є такою якою є, і саме в них міститься інформація про об’єкт вивчення. Досить часто обсяг отриманих при конкретних умовах вибіркових значень є єдиною інформацією про досліджуваний об’єкт. Іншими словами, якщо експеримент закінчено, то вже жодні інші дані, які отримані про цей об’єкт поза часом експерименту не можуть бути використані, оскільки вони вже належать іншій ситуації.

Врахувати всі фактори, які можуть впливати на поведінку об’єкта, в процесі проведення експерименту, та на результати вимірювань є практично неможливо, але цілком зрозуміло, що вони будуть містити принаймні дві випадкові складові, зумовлені внутрішніми (системними) та

2

зовнішніми (реєстраційними) чинниками. В загальному, отримані дані, а точніше їх конкретні значення, в будь-яких дослідженнях, можна представити такою моделлю

де mx – математичне сподівання або деяка умовно чи теоретично встановлена величина, яка «ідеалізує» значення вимірюваного показника; F xi – випадкова величина з індивідуальним для об’єкта вивчення розподілом, яка змінюється в межах від нуля до деякого значення xmax і характеризує зміну величини xi за рахунок зміни стану об’єкта, через дії внутрішніх та зовнішніх чинників; i – випадкова величина яка характеризує помилки вимірювання та випадковий вплив

середовища на процес вимірювання.

В цьому плані, врахування впливаючих на стан об’єкта та процес вимірювання різних чинників, можна розглянути на моделі результатів експерименту, відображений в ній перерозподіл

випадкові зміни в стані об’єкта вивчення та характеризують процес вимірювання. Очевидно, що в i k

такий спосіб можна врахувати і більше як два фактори, прийнявши i 1. Тоді в (2), всі i 1

доданки починаючи з другого, які враховані в (1) сумою F xi i дадуть, в загальному, випадкову величину з багатомодовим розподілом. Це означає, що ми ніколи не зможемо отримати значення xi , які б точно збігалися з відомими конкретними законами розподілів. Цей факт завжди

треба мати на увазі при виборі вигляду функції для апроксимації нею емпіричної функції розподілу (гістограми).

Варіаційний ряд

Найпростішим видом подання статистичної сукупності даних, тобто, отриманих в той чи інший спосіб чисел, які характеризують досліджувану ознаку чи параметр досліджуваного обʼєкта, явища, процесу є варіаційний ряд. Його особливістю є те, що числа значень отриманої сукупності даних знаходяться в порядку зростання (спадання) їх величин. Такий ряд, а точніше його обвідна, дає загальну картину розподілу випадкових значень отриманих даних. Саме ранжування – розташування в порядку зростання значень даних, дає підстави виявити, яка закономірність закладена в розподілі та, навколо якої величини концентруються варіанти – елементи вибірки. Ряди, впорядковані за зростанням значень варіант характеризують структуру (склад) досліджуваного явища, дають змогу судити про однорідність сукупності та про варіювання досліджуваної ознаки, а також визначити загальні кількісні характеристики цієї вибірки.

Варіаційний ряд дає можливість наочно і швидко сприйняти структуру даних, а саме: варіанти значень xi , які може приймати і приймає змінна X ;

- кількість відповідних варіант ni ;

- мінімальні xmin та xmax максимальні значення;

- безпосередньо оцінити основні показники вибірки – моду і медіану, квартилі. Представлення даних варіаційним рядом є підготовчим етапом до розрахунків і побудови

статистичних розподілів досліджуваної змінної.

Варіаційний ряд для задач обробки даних має надзвичайно важливе і переважно вирішальне значення. Формально, зміст варіаційного ряду можна подати в такий спосіб. Нехай, в результаті

3

експериментів отримано N випадкових величин, що характеризують значення спостережень, тобто отримано вибірку даних обсягом N , яку можна представити множиною X значень її варіант в такий спосіб:

X x1, x2 , , xN xi :i 1, N .

Для варіаційного ряду цей вираз можна записати в такій спосіб

~ X N x 1 x 2 x N ,

де значок тильда означає перетворення сортування, причому таке, що x 1 min (x1 , , x N ) , а

x N max (x1 , , xN ) .

Отримана в результаті сортування послідовність формальним поданням варіаційного ряду. Величину x i називають i -ою порядковою статистикою або i -ою варіантою варіаційного ряду.

Переважно випадкові величини xi є незалежними і однаково розподіленими, натомість величини x i є вже залежними завдяки, отриманій впорядкованості між ними.

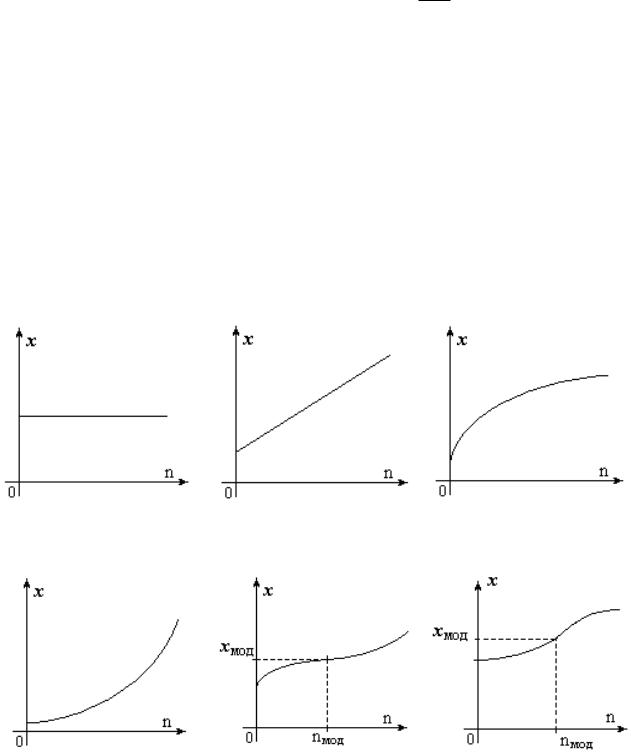
Найбільшу інформацію про характер закону розподілу значень варіант несе обвідна варіаційного ряду. На рис. 1 представлені типові зображення обвідних варіаційних рядів.

Рис. 1. Види обвідних варіаційних рядів: а – для постійних за величиною значень; б – за рівномірного розподілу, в і г - нелінійні розподіли за відсутності моди; д і е – одномодові розподіли.

4

Крім того, графічне подання варіант варіаційного ряду дає можливість вияснити, а часом і визначити такі характеристики:

-розмах, як різницю між найбільшим і найменшим значеннями варіант;

-вказати тип розподілу, до якого відноситься розподіл варіант даного варіаційного ряду;

-просто встановити значення квантилів, зокрема квартилів та медіани (другого квартиля);

-вказати на присутність або відсутність моди;

-присутність кількох точок перегину вказує на багатомодовий вид розподілу;

-вказати на асиметрію розподілу.

За достатнього досвіду можна значно розширити цей перелік властивостей вибірки. До основних характеристик варіаційного ряду відносять:

обсяг вибірки N ;

екстремальні значення x 1 та x N ;

розмах W x( N ) x(1) ;

максимальне відхилення x(i) xi від вибіркового середнього x ;

розмах варіаційного ряду R x N x 1 ;

мода – xmod – значення, що найчастіше зустрічається в вибірці;

медіана – xmed – значення, яке ділить варіаційний ряд на дві однакові за кількістю елементів частини;

Обвідна варіаційного ряду X n є не спадною монотонною функцією, оскільки для будьяких двох точок n1 n2 має місце X n1 X n2 . В реальних даних це зростаюча східчаста

функція з випадковою висотою, рівною максимальному значенню варіанти даної сукупності. Висота сходинок визначається кількістю однакових значень у даному інтервалі вибірки.

Можна виділити шість видів обвідних, форми яких представлені на рис.1., в залежності від закону розподілу випадкових величин.

Для рядів з формою обвідної, як на рис.1а, обвідна вказує на те що дані майже не змінюються і є близькими до константи. Дані представлені варіаційними рядами на рис. 1б – 1г належать відповідно рівномірному, логарифмічному та екпоненційному типам розподілів. Характерним для них є те, що вони представляють випадкові змінні з законами розподілів, які не мають моди, тобто ці обвідні не мають точок перегину. Обвідні на рис.1д і 1е мають точки

перегину з координатами nмод ; xмод , які визначають з рівняння d 2X n 0 . dn2

Якщо не повторюючи елементів варіаційного ряду xi для кожного з них вказати відносну частоту його появи pi mNi , враховуючи кількість однакових значень, тобто mi 1, 2, , то

такий варіаційний ряд є дискретним розподілом випадкової величини, отриманих спостережень. Тому на основі варіаційного ряду досить легко побудувати емпіричну функцію розподілу

N

значень менших за xi , Fn x – східчаста не спадна функція, причому висота сходинок є рівна

частоті pi .

Для варіаційного ряду (1) функцію Fn x можна записати такими співвідношеннями

5

Подання даних у вигляді варіаційного ряду показує на присутність серед варіант значень, що дуже сильно відрізняються від основної маси спостережень. Такі дані називають викидами. Більшість традиційних статистичних методів є вельми чутливі до таких значних відхилень значень варіант. Тому викиди можуть не тільки спотворити значення вибіркових показників, але і привести до помилкових висновків.

Підозра про присутність таких спостережень повинно виникнути, якщо вибіркова медіана сильно відрізняється від вибіркового середнього, хоча в цілому сукупність симетрична, або, якщо положення медіани є дуже несиметричне щодо мінімального і максимального елементів вибірки. Тому, найпростіше виявляти викиди за допомогою переходу від вибірки до варіаційного ряду.

Ще однією дуже важливою властивістю варіаційного ряду є те, що положення точки перегину вказує на симетричність розподілу. Якщо точка перегину знаходиться всередині варіаційного ряду, а відхилення по обидві сторони від точки перегину по осі ординат є практично однакові, тоді розподіл є симетричним.

Другою особливістю є встановлення ексцесу – коефіцієнта, який характеризує «крутість», тобто, стрімкість підвищення кривої розподілу у порівнянні з нормальною кривою, за характером ділянки варіаційного ряду всередині якої знаходиться точка перегину. Якщо точка перегину лежить в середині лінійної ділянки варіаційного ряду, причому досить великої, можна стверджувати таке. Якщо ексцес деякого розподілу відмінний від нуля, то крива щільності цього розподілу відрізняється від кривої щільності нормального розподілу. Якщо ексцес додатній, то крива цього розподілу має «гострішу» вершину ніж крива нормального, а якщо ексцес від'ємний, то то його крива має «плоскішу» вершину ніж крива нормального. При цьому вважається, що нормальний і даний розподіли мають однакові арифметичні середні та дисперсії.

Приклад. В табл. 1 приведені значення елементів деякої вибірки.

Наприклад, це може бути щоденна кількість відвідувачів бібліотеки, кількість книжок у видачі тощо. Приведена вибірка має обсяг рівний N 60 елементів. Елементами є цілі числа, що

6

відповідають щоденній кількості відвідувачів читального залу деякої бібліотеки протягом 60 днів. Курсивом виділено порядок днів, жирним – кількість відвідувачів.

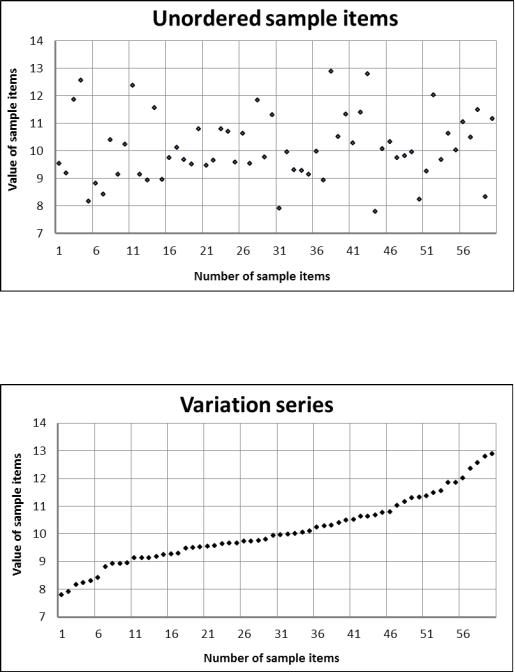
На рис. 2. зображено точками значення елементів цієї вибірки даних у відповідності з порядком їх отримання.

Рис. 2. Послідовність отриманих лементів вибірки, що мають кількісний характер.

На рис. 3 графічно зображений варіаційний ряд для вибірки на рис. 2.

Рис. 3. Варіаційний ряд вибірки з рис. 2.

Простий візуальний аналіз графіка варіаційного ряду на рис. 3 дає таку інформацію. По-перше, вибірка має моду, а по-друге є практично є симетричною. Функція щільності має

дещо приплюснута, оскільки є багато значень дуже близьких до значення моди. значення ексцесу є відʼємним, оскільки обвідна в середині ряду (між двома квартелями) має прямолінійний характер.

Описова статистика

7

Одним з пріоритетних завдань математичної статистики є встановлення виду закону розподілу значень елементів даної сукупності та визначення його параметрів. Це досить складна задача. Проте, апріорну характеристику даних, на першому кроці аналізу, дає описова статистика.

Методами описової статистики називаються методи опису вибірок Х1, Х2, ..., Хn за допомогою різних показників і графіків. Перевага методів описової статистики в тому, що її прості і досить інформативні статистичні показники позбавляють від необхідності перегляду великої кількості значень вибірки.

Описова статистика займається дослідженням структури вибірки як чогось цілого. Метою описової статистики є представлення отриманого масиву даних у такій компактній формі, яка би володіла максимумом інформативності щодо цих даних. В цьому випадку, отримані дані можуть бути охарактеризовані простими засобами математичної статистики. Вони дають можливість подати представлення про особливості отриманої вибірки щодо перспективи використання більш глибоких методів аналізу.

Описова статистика − це набір основних статистичних показників емпіричної вибірки. Загалом для того, щоб передати максимум інформації про певні особливості об’єктів вибірки, використовують три типи характеристик: центру, масштабу та форми розподілу вибірки. Методи розрахунку цих показників, як правило, розроблені, на основі припущення, що розподіл варіант такої вибірки є нормальним. Тому, перш ніж приступити до визначення параметрів включених в описову статистику, необхідно перевірити відповідність елементів вибірки нормальному закону розподілу.

До кількісних характеристик відносять числові характеристики: середнє значення, середнє квадратичне відхилення, коефіцієнт варіації та моменти.

Центр статистичного розподілу характеризують його середнє значення, медіана та мода. Якщо усі ці три параметри збігаються, тоді має місце симетричний, переважно нормальний закон розподілу, але якщо вони відрізняються між собою розподіл характеризується певною величиною асиметрії.

Асиметрія є додатною, якщо значення моди перевищує значення медіани або від᾽ємною, тобто, значення медіани перевищує значення моди.

Крім того, можна дати і характеристику ексцесу. Якщо відрізок обвідної між першим і третім квартилем, середина якого збігається з точкою перегину (з модою), апроксимований прямою лінією має незначний кут нахилу ексцес є значним. Чим меншим є такий відрізок, тим меншим є ексцес.

Описова статистика дає досить загальну відповідь щодо характеристики розподілу сукупності даних. Ці характеристики є групами параметрів і кількісно описують загальну структуру розподілу. До них відносять такі:

- міри центральної тенденції – характеристики положення (середнє арифметичне, медіана,

мода);

-міри розкиду даних – характеристики розсіювання (дисперсія, середньоквадратичне відхилення, коефіцієнт варіації, розмах);

-показники асиметрії і ексцесу.

Міри центральної тенденції

Міри центральної тенденції – це такі величини у вибірці, навколо яких групуються інші дані. Вони показують загальні характеристики розподілу даних за певною змінною, дозволяють виявити одне значення або кілька значень, що описують весь розподіл. Ці величини є як би узагальнюючими для всієї вибірки показниками, що, по-перше, дозволяє на підставі них судити про всю вибірку, а по-друге, вони дають можливість порівнювати різні вибірки між собою. До мір центральної тенденції відносять: середнє арифметичне, медіану, моду, середнє геометричне, середнє гармонічне. Можна також сказати, що середнє, мода та медіана — це окремі значення що представляють весь набір даних. У статистиці вони є типовими для всіх досліджуваних груп.

Міри центральної тенденції потрібні з наступних міркувань:

8

-отримати загальну картину розподілу, оскільки неможливо запам’ятати кожен факт, що стосується сфери дослідження.

-отримати чітку картину щодо досліджуваної сфери для розуміння та отримання потрібних висновків.

-отримати чіткий опис групи в цілому та мати змогу порівнювати дві або більше груп у термінах типової для них «поведінки».

Середнє арифметичне значення (Mean). Представлення даних у вигляді таблиць і діаграм є суттєвою, але не основною частиною аналізу даних. Головна роль належить методам дослідження числових значень даних та їх властивостей. В більшості випадків дані концентруються навколо деякої точки – середньої величини. Середня величина є найбільш поширеною формою статистичних показників. Вона фактично є узагальненою кількісною характеристикою ознаки сукупності даних за конкретних умов місця і часу. Показник у формі середньої величини відображає типові риси і дає узагальнену характеристику однотипних явищ за однією з варіюючих ознак. Значення окремих одиниць сукупності для даної ознаки можуть коливатися в ту чи іншу сторону під впливом як основних, так і випадкових факторів. Сутність середньої полягає в тому, що в ній взаємно нейтралізуються відхилення значень окремих одиниць сукупності даних щодо ознаки, зумовлені дією випадкових факторів, і враховуються зміни, викликані дією основних

Середньою величиною в статистиці називають показник, який характеризує типовий розмір варіюючої ознаки в якісно однорідній сукупності даних. Переважно, роль цієї середньої величини виконує середнє арифметичне (arithmetic mean) значення. Середнє арифметичне є таким значенням ознаки, для якого сума відхилень окремих значень цієї ознаки рівна нулю. Геометричний зміст середнього арифметичного полягає в тому що його значення є точкою на абсцисі, яка відповідає центру мас. Іншими словами, середнє значення ознаки залежить від суми значень усієї статистичної сукупності. При цьому, якщо індивідуальні значення ознаки в даній сукупності замінити середньою арифметичною, то сумарний обсяг ознаки для цієї сукупності залишиться незмінним. Це означає, що середня арифметична і є середньою величиною. Її обчислюють за такою формулою:

1n

xn xi ,

i1

де xi − значення величини варіанти даної вибірки, n – кількість варіант у вибірці.

Середня арифметична є найбільш розповсюдженим видом середніх величин і, використовується в тих випадках, коли обсяг даних усереднюваної ознаки є адитивною величиною.

Оскільки середнє арифметичне залежить від усіх елементів сукупності, наявність екстремальних значень суттєво впливає на результат. В таких випадках середнє арифметичне може значно спотворити зміст числових даних.

Є певні загальні правила для використання середнього, зокрема:

-середнє – це «центр тяжіння» розподілу, і кожне значення дає внесок у його визначення;

-середнє значення є більш узагальнюючим ніж медіана чи мода. Тому, коли потрібно знайти найбільш загальну міру центральної тенденції, використовують саме середнє.

Переваги середнього:

Середнє визначене дуже жорстко, тому не виникає питань чи нерозуміння щодо його значення та суті.

Це найбільш поширена міра центральної тенденції, оскільки її легко зрозуміти. Середнє легко підрахувати.

Враховує всі значення вибірки.

Обмеження середнього:

На значення середнього впливають екстремальні значення. Часом середнім є величина значення, що не присутня у вибірці.

9

Інколи результатом можуть бути абсурдні значення. Наприклад, середнє цілих чисел є дробовим (середня кількість відвідувачів за день протягом тижня може бути дробовим числом).

Медіана. Медіана є числовою характеристикою випадкової величини і відповідає такій умові. Якщо варіанта x(i) з імовірністю p 0.5 може набувати значення як більші за медіану, так

і менші за неї, то вона є медіаною, тобто x i xmed . Отже, медіана є серединним значенням

впорядкованої сукупності однорідних даних, причому половина значень виявиться меншими за медіану, а половина – більшими. Якщо в сукупність містить екстремальні значення, то для оцінки середнього значення краще використовувати не середнє арифметичне, а медіану. Для обчислення медіани спочатку необхідно впорядкувати сукупність, наприклад, в зростаючому порядку.

Якщо кількість варіант даного варіаційного ряду є непарною, то його медіаною є той його

приймати за медіану середню арифметичну двох сусідніх членів в середині варіаційного ряду

До основних характеристичних властивостей медіани належать такі:

1.Кількість додатних відхилень від медіани рівна кількості від’ємних відхилень. Ця властивість медіани є прямим наслідком її визначення.

2. Сума абсолютних значень відхилень від медіани є найменшою. Для чого використовують медіану?

- Коли потрібно знайти точну середню точку, точку на «півдорозі» від найменшого значення до найбільшого.

-Коли екстремальні значення впливають на середнє – медіана є найкращою мірою центральної тенденції.

-Медіану використовують коли потрібно, щоб певні значення впливали на центральну тенденцію, але все, що про них відомо – що вони менші або більші за медіану.

Переваги медіани:

-легко вирахувати та зрозуміти.

-для підрахунку медіани не потрібні всі значення в розподілі.

-екстремальні значення розподілу не впливають на медіану.

Обмеження медіани:

-вона не так жорстко визначена як середнє, оскільки її значення не обчислюється, а визначається шляхом впорядкування даних;

-не враховує всі спостереження;

-з медіаною не можна робити алгебраїчні перетворення так, як із середнім.

-потребує впорядкування значень.

Квартилі. В доповнення до медіани для характеристики структури варіаційного ряду, вираховують квартилі, які поділяють цей ряд на 4 рівні частини, які також є числовими характеристиками даної вибірки. Квартилі - це показники, які найчастіше використовуються для

10