3.4.1. Непараметрические модели коллективного типа, основанные на учёте оценки эффективности упрощённых аппроксимаций

С целью повышения аппроксимационных свойств непараметрических моделей коллективного типа в условиях большого уровня зашумлённости и наличия выбросов в исходных экспериментальных данных возникает задача дополнительного сглаживания модели восстанавливаемой зависимости (3.1). Предлагается учитывать статистические оценки эффективности упрощённых параметрических аппроксимаций . В качестве показателя эффективности -ой аппроксимации может выступать среднеквадратический критерий

, .

Учёт эффективности целесообразно осуществить введя в коллективную модель (3.25) ядерную меру близости между значением и её минимальным значением (нулём). В результате полученная модификация непараметрической модели коллективного типа (3.25) с учётом оценок эффективности упрощённых параметрических аппроксимаций имеет вид

,

где - параметр ядерной функции , который характеризует область её определения.

3.4.2. Асимптотические свойства непараметрической модели коллективного типа

Для удобства последующего анализа предположим, что - скаляр и закон распределения известен, а опорные функции - линейные. Тогда непараметрическая модель коллективного типа принимает вид

(3.28)

Запишем оценку непараметрической модели коллективного типа (3.28) с учётом выражения (3.27) в виде статистики

,

которая позволяет упростить методику исследования асимптотических свойств .

Теорема 3.2. Пусть: 1) и , в области определения ограничены и непрерывны со всеми своими производными до второго порядка включительно; 2) ядерные функции являются положительными, нормированными и симметричными, а также ; 3) последовательность при , а . Тогда непараметрическая модель коллективного типа обладает свойствами асимптотической несмещённости и состоятельности.

Асимптотические выражения смещения оценки (3.28) и её среднеквадратического отклонения после стандартных аналитических преобразований принимают вид

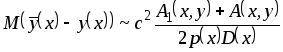, (3.29)

, (3.30)

где , - нелинейные функционалы от и их производных; - дисперсия опорных точек; .

Из асимптотических выражений (3.29), (3.30) при и следует асимптотическая несмещённость и сходимость в среднеквадратическом непараметрической модели коллективного типа .

Установлено, что асимптотические свойства непараметрических моделей коллективного типа «слабо» зависят от вида упрощённых аппроксимаций и объёма выборки в задаче их идентификации. Эффективность рассматриваемых моделей в значительной степени определяется законом распределения системы опорных точек и их количеством.

Данные выводы подтверждает выражение минимального среднеквадратического отклонения при оптимальном значении параметра размытости

(3.31)

3.4.3. Оптимизация непараметрических моделей коллективного типа

Проблема оптимизации непараметрических моделей коллективного типа охватывает определение рационального закона распределения «опорных» точек, выбор оптимальных коэффициентов размытости и ядерных функций.

Выбор оптимальной ядерной функции осуществляется по аналогии с пунктом 3.3.2. При этом установлено, что оптимальным с смысле минимума среднеквадратического отклонения является ядро Епанечникова

Оптимизация непараметрических моделей коллективного типа осуществляется по аналогии с непараметрической оценкой регрессией (пункт 3.3.3).

Выбор закона распределения опорных точек. Выбор рационального закона распределения опорных точек осуществляется, основываясь на основных положениях теории вероятностей, путем решения следующей вариационной задачи

,

,

где - асимптотическое выражение среднеквадратического критерия (3.31).

В соответствии с результатами решения данной задачи рекомендуется выбирать «опорные» точки с законом распределения

повторяющим вид восстанавливаемой зависимости, что позволяет минимизировать главную составляющую дисперсии . При этом большая часть «опорных» точек формируется в области больших значений восстанавливаемой функции и её производных.

Итерационная процедура формирования упрощённых аппроксимаций. Пусть - некоторая система упрощённых аппроксимаций зависимости построенная относительно «опорных» точек . При этом эмпирическая ошибка расхождения между экспериментальными данными и строящейся непараметрической моделью

,

где - множество номеров точек не входящих в число «опорных» ; - множество номеров точек исходной выборки.

Вклад слагаемых в формирование эмпирической ошибки неравнозначный. Если модель в некоторой точке имеет максимальное расхождение с экспериментальным значением , то естественно было бы принять точку в качестве «опорной» при построении -ой упрощённой аппроксимации. Однако существующая невязка может быть связана с ошибкой системы контроля. Для проверки данной гипотезы можно воспользоваться условием непрерывности: близким значениям аргумента соответствуют близкие значения функции.

Методика формирования системы «опорных» точек модели представляется следующей последовательностью действий:

1. Выбрать в качестве первой «опорной» -ю точку с максимальным значением функции либо её производной. Принять значение параметра .

2. Включить номер -й «опорной» точки в множество .

3. Оценить параметры упрощённой параметрической аппроксимации .

4. Построить непараметрическую модель коллективного типа .

5. Проверить соответствие количества опорных точек требуемому либо заданной оценке точности аппроксимации. Если условие выполнено, то процесс заканчивается.

6. Определить новую опорную точку из условия

.

Принять и перейти к этапу 2.

Комбинированная процедура формирования упрощённых аппроксимаций. В процессе исследований непараметрических моделей коллективного типа возникла идея создания метода формирования упрощённых аппроксимаций, учитывающих преимущество рационального метода и итерационной процедуры формирования опорных точек. Итерационная процедура обусловлена значительными временными затратами, а рациональный закон распределения сложен в реализации. Поэтому предлагается комбинированная процедура формирования упрощённых аппроксимаций.

Идея предлагаемого подхода формирования последовательности опорных точек основывается на их моделировании с равномерными законом распределения и последующей доводкой с помощью итерационной процедуры выбора упрощённых аппроксимаций, минимизирующих на каждом этапе относительную эмпирическую ошибку между восстанавливаемой зависимостью и её коллективной моделью.

Предлагаемая методика:

1. Выбрать из обучающей выборки с помощью датчика случайных чисел опорных точек .

2. Оценить оптимальные параметры моделей из условия

,

где - множество номеров точек не входящих в число опорных.

3. Построить непараметрическую модель коллективного типа

,

где - нормированное расстояние между точками либо ядерная функция.

4. Определить следующую опорную точку из условия

.

5. Оценить оптимальные параметры модели

.

Далее принять и перейти к этапу 3. Так продолжать до тех пор, пока ошибка восстановления не будет удовлетворять пользователя.