
- •3.1. Классификация методов восстановления стохастических зависимостей
- •3.2. Параметрические алгоритмы восстановления стохастических зависимостей
- •3.3. Непараметрическая оценка регрессии в задаче восстановления стохастических зависимостей
- •3.3.1. Асимптотические свойства непараметрической оценки регрессии
- •Распишем выражение
- •3.3.2. Оптимизация непараметрической оценки регрессии по виду ядерной функции
- •3.3.3. Оптимизация непараметрической оценки регрессии по коэффициенту размытости
- •3.4. Непараметрические модели коллективного типа в задаче восстановления стохастических зависимостей
- •3.4.1. Непараметрические модели коллективного типа, основанные на учёте оценки эффективности упрощённых аппроксимаций
- •3.4.2. Асимптотические свойства непараметрической модели коллективного типа
- •3.4.3. Оптимизация непараметрических моделей коллективного типа
- •3.4.4. Оптимизация непараметрических моделей коллективного типа по коэффициенту размытости
- •3.5. Нелинейные непараметрические коллективы решающих правил в задаче восстановления стохастических зависимостей
- •3.6. Гибридные модели в задаче восстановления стохастических зависимостей
- •3.7. Синтез и анализ гибридных моделей стохастических зависимостей в условиях наличия их частного описания
- •3.8. Непараметрические гибриды решающих правил в задаче восстановления стохастических зависимостей
- •3.9. Последовательные процедуры формирования решений, основанные на учёте функций невязок
- •3.10. Коллективы решающих правил, основанные на учёте их условий компетентности
- •Литература
- •Дополнительная литература
- •Контрольные вопросы
- •Контрольные упражнения
Распишем выражение
![]()
![]()
Рассмотрим отдельно второе и третье слагаемое:
-
Подставим в удвоенное произведение выражение (3.8), тогда
![]()
-
 ;
;
Рассмотрим первое слагаемое

 .
.
Двойную сумму
можно представить в виде квадратной
матрицы с
![]() - столбцами и
- столбцами и
![]() - строками. Выделим главную диагональ
матрицы
- строками. Выделим главную диагональ
матрицы
![]() и все остальные элементы
и все остальные элементы
![]()
 .
.
(3.9)
Рассмотрим данное выражение (3.9) по частям, сначала слагаемое соответствующее главной диагонали матрицы

 .
.
Учитывая, что
![]() наблюдения одной
и той же случайной величины
наблюдения одной
и той же случайной величины
![]() ,
поэтому
,
поэтому
![]() .
.
Тогда


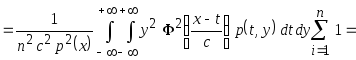
 .
.
Представим
совместную плотность вероятности
![]() в виде произведения
в виде произведения
![]() и выделив квадрат условного математического
ожидания
и выделив квадрат условного математического
ожидания
 ,
получаем
,
получаем


 .
.
После замены
переменных
![]() ,
,
![]() ,
,
![]() и т.д., получаем
и т.д., получаем


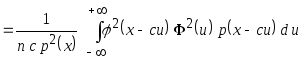 .
.
Разложим функции
![]() и
и
![]() в ряд Тейлора в точке
в ряд Тейлора в точке
![]() до второй производной. Тогда
до второй производной. Тогда




 .
.
Заметим, что 3-е
слагаемое в первой скобки содержит
отношение
![]() .
Если
.
Если
![]() ,
а
,
а
![]() ,
то отношение
,
то отношение
![]() очень мало. Поэтому для упрощения
дальнейших выкладок будем пренебрегать
ими. Тогда получим
очень мало. Поэтому для упрощения
дальнейших выкладок будем пренебрегать
ими. Тогда получим



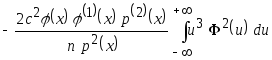 .
.
Так как
 и
и
 ,
а слагаемыми с коэффициентом
,
а слагаемыми с коэффициентом
![]() несоизмеримо малы, то выражение,
соответствующее элементам главной
диагонали матрицы имеет вид
несоизмеримо малы, то выражение,
соответствующее элементам главной
диагонали матрицы имеет вид
 .
.
Рассмотрим второе слагаемое выражения (3.9)

 .
.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, поэтому данное выражение принимает вид

 .
.
Учитывая, что
![]() и
и
![]() наблюдения одной и той же случайной
величины
наблюдения одной и той же случайной
величины
![]() ,
тогда
,
тогда
![]() .
.
Тогда


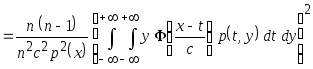 .
.
При
![]() отношение
отношение
![]() .
Внесём
.
Внесём
![]() под квадрат, а совместную плотность
вероятности
под квадрат, а совместную плотность
вероятности
![]() представим в виде произведения
представим в виде произведения
![]() ,
получим
,
получим
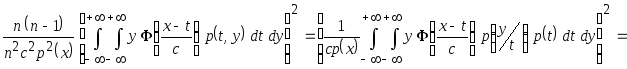
 .
.
Заметим, что
полученное выражение соответствует
квадрату математического ожидания
![]()
 .
.
Раскрывая квадрат
и пренебрегая слагаемыми малости
![]() ,
получим
,
получим
![]()
![]()
![]() .
.
В итоге выражение, соответствующее среднеквадратическому отклонению, имеет вид
![]()

![]()
 .
.
Вычислим интегральное выражение среднеквадратического отклонения

 .
(3.10)
.
(3.10)
Оптимальный коэффициент размытости, минимизирующее интегральное среднеквадратическое отклонение
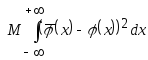 ,
,
определяется по формуле
 .
(3.11)
.
(3.11)
Из полученного
выражения следует, что
![]() .
.
3.3.2. Оптимизация непараметрической оценки регрессии по виду ядерной функции
Выбор оптимальной ядерной функции осуществляется по аналогии с пунктом 2.2.2.3. Подставляем в интегральное выражение среднеквадратического отклонения (3.10) выражение соответствующее оптимальному коэффициенту размытости (3.11). В результате имеем
 .
.
Следовательно, задача минимизации данного выражения сводится к решению вариационной задачи (см. параграф 2.2.2.3)
 ,
,

В результате получаем ядерную функцию Епанечникова

3.3.3. Оптимизация непараметрической оценки регрессии по коэффициенту размытости
При фиксированном объёме статистических данных качество аппроксимации стохастических зависимостей с помощью непараметрической оценки регрессии существенно зависит от выбранных коэффициентов размытости ядерных функций.
Определение
конкретных значений коэффициентов
размытости
![]() обычно осуществляется из условия
минимума эмпирических критериев:
обычно осуществляется из условия
минимума эмпирических критериев:
средняя ошибка аппроксимации
 ;
;
среднеквадратическая ошибка аппроксимации
 ;
(3.12)
;
(3.12)
средняя относительная ошибка аппроксимации
 ;
(3.13)
;
(3.13)
среднеквадратическая относительная ошибка аппроксимации
 .
.
В преимущество
критерия (3.13) состоит в том, что умножив
его величину на 100%, получим ошибку
аппроксимации в процентном соотношении
с диапазоном изменения
![]() .
Иначе говоря, значение критерия не
зависит от единиц измерения
.
Иначе говоря, значение критерия не
зависит от единиц измерения
![]() .
Основной его недостаток заключается в
том, что если
.
Основной его недостаток заключается в
том, что если
![]() может принимать нулевые значения либо
близкие к ним возникает неоднозначность
и значения критерия могут значительно
превышать 100%.
может принимать нулевые значения либо
близкие к ним возникает неоднозначность
и значения критерия могут значительно
превышать 100%.
В отличие от (3.13)
критерий (3.12) может быть использован в
любых ситуациях, но его значения зависят
от единиц измерения
![]() ,
что затрудняет количественную оценку
ошибки аппроксимации.
,
что затрудняет количественную оценку
ошибки аппроксимации.
Метод
скользящего экзамена. Выбор
оптимального коэффициента размытости
осуществляется по элементам обучающей
выборки. Идея метода заключается в том,
что последовательно каждая
![]() -я
точка исходной обучающей выборки
принимается в качестве контрольной
ситуации с последующим исключением её
из процесса обучения. Рассмотрим данный
процесс на примере критерия (3.12)
-я
точка исходной обучающей выборки
принимается в качестве контрольной
ситуации с последующим исключением её
из процесса обучения. Рассмотрим данный
процесс на примере критерия (3.12)
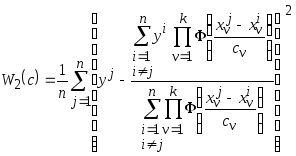 .
(3.14)
.
(3.14)
Условие
![]() позволяет исключить
позволяет исключить
![]() -ю
контрольную точку из процесса обучения.
При этом оптимальный набор коэффициентов
размытости
-ю
контрольную точку из процесса обучения.
При этом оптимальный набор коэффициентов
размытости
![]() будет соответствовать минимальному
значению критерия
будет соответствовать минимальному
значению критерия
![]()
![]() .
.
Для упрощения
задачи выбора оптимального коэффициента
размытости можно воспользоваться
методикой представленной в пункте
2.2.2.2., что позволяет свести задачу
оптимизации к нахождению всего лишь
одного параметра
![]() .
.
Рассчитаем по обучающей выборки оценки среднеквадратического отклонения
 ,
,
которые характеризуют диапазон изменения признаков.
Сопоставим каждому
коэффициенту размытости
![]() произведение
произведение
![]() ,
где неопределённый коэффициент
,
где неопределённый коэффициент
![]() будет общим для каждого признака. В
результате получим
будет общим для каждого признака. В
результате получим
![]() .
.
При этом среднеквадратический критерий (3.14) будет иметь вид
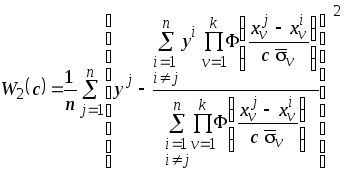 .
(3.15)
.
(3.15)
Зависимость
эмпирического критерия
![]() от коэффициента размытости представлена
на рис. 3.4.
от коэффициента размытости представлена
на рис. 3.4.

Рис. 3.4. Зависимость
ошибки аппроксимации (3.12) от величины
коэффициента размытости для одномерного
случая (![]() - скаляр).
- скаляр).
Кривая 1 соответствует
объёму обучающей выборки
![]() ,
,
кривая 2 -
![]() ,
кривая 3 -
,
кривая 3 -
![]() .
.
Метод
деления выборки на контрольную и
обучающую. Идея
метода состоит в декомпозиции исходной
обучающей выборки на контрольную
![]() и обучающую
и обучающую
![]() выборки
выборки

где
![]() - объём обучающей выборки, а
- объём обучающей выборки, а
![]() - контрольной.
- контрольной.
При этом среднеквадратический критерий (3.12) будет иметь вид
 .
.
Данный критерий
характеризует среднеквадратическое
расхождение между строящейся по выборке
![]() непараметрической регрессией и элементами
контрольной выборки
непараметрической регрессией и элементами
контрольной выборки
![]() .
.
Рассматриваемый
метод поиска оптимального коэффициента
размытости наиболее удобно применять
при достаточно больших объёмах обучающей
выборки (более 200 наблюдений на каждый
признак
![]() ),
когда исследователь может пожертвовать
частью исходной выборки
),
когда исследователь может пожертвовать
частью исходной выборки
![]() и сформировать контрольную
и сформировать контрольную
![]() .
.
Метод случайного
поиска коэффициентов размытости. Данный
метод основан на случайном выборе
оптимального вектора
![]() из множества альтернатив, которое
генерируется с использованием датчиков
случайных величин.
из множества альтернатив, которое
генерируется с использованием датчиков
случайных величин.
Запишем непараметрическую оценку регрессии (3.5) в виде
 .
(3.16)
.
(3.16)
Из вычислительных
экспериментов установлено, что
коэффициенты
![]() ,
,
![]() в выражении (3.16) принадлежит интервалу
в выражении (3.16) принадлежит интервалу
![]() .
.
Для генерации
множества векторов
![]() воспользуемся датчиками случайных
величин с равномерными законами
распределения на интервале
воспользуемся датчиками случайных
величин с равномерными законами
распределения на интервале
![]()
![]() ,
,
где
![]() - случайная величина с равномерным
законом распределения,
- случайная величина с равномерным
законом распределения,
![]() - величина близкая к нулю (например
- величина близкая к нулю (например
![]() ),
а
),
а
![]() можно принять равным трём. В результате
данной операции получим выборку
можно принять равным трём. В результате
данной операции получим выборку
![]() ,
которую при
,
которую при
![]() можно отобразить на рис. 3.5.
можно отобразить на рис. 3.5.

Рис. 3.5. Выборка
векторов
![]() при
при
![]() .
.
Последовательно подставляя полученные вектора в среднеквадратический критерий
 ,
,
получим выборку
![]() и выберем тот вектор
и выберем тот вектор
![]() ,
при котором
,
при котором
![]() будет минимальна.
В окрестности
будет минимальна.
В окрестности
![]() генерируются новые вектора
генерируются новые вектора
![]() и находится наилучший на данном этапе
набор параметров
и находится наилучший на данном этапе
набор параметров
![]() .
Описанный процесс продолжается до тех
пор пока изменения критерия будут
незначительными.
.
Описанный процесс продолжается до тех
пор пока изменения критерия будут
незначительными.
Рандомизированный
метод оптимизации непараметрической
оценки регрессии.
Существующий парадокс традиционных
методов идентификации стохастических
моделей состоит в сопоставлении случайной
выборке наблюдений
![]() переменных изучаемого объекта конкретного
набора параметров модели оптимальных
в смысле минимума эмпирической
ошибкиаппроксимации. Рассмотрим
принципиально новый рандомизированный
подход оптимизации непараметрических
алгоритмов, основанный на процедуре
случайного выбора коэффициентов
размытости ядерных функций из некоторой
генеральной совокупности с определённым
законом распределения. В этом случае
непараметрическая оценка регрессии
принимает вид
переменных изучаемого объекта конкретного
набора параметров модели оптимальных
в смысле минимума эмпирической
ошибкиаппроксимации. Рассмотрим
принципиально новый рандомизированный
подход оптимизации непараметрических
алгоритмов, основанный на процедуре
случайного выбора коэффициентов
размытости ядерных функций из некоторой
генеральной совокупности с определённым
законом распределения. В этом случае
непараметрическая оценка регрессии
принимает вид
 ,
,
где коэффициент
размытости
![]() является случайной величиной с плотностью
вероятности
является случайной величиной с плотностью
вероятности
![]() и соответствует наблюдению
и соответствует наблюдению
![]() .
.
Из анализа
асимптотических свойств непараметрической
регрессии следует, что нижняя граница
области изменения коэффициента размытости
с ростом объёма выборки
![]() стремится к нулю. Отсюда возникает идея
оптимизировать непараметрическую
оценку регрессии по виду закона
распределения
стремится к нулю. Отсюда возникает идея
оптимизировать непараметрическую
оценку регрессии по виду закона
распределения
![]()
![]()
![]() коэффициентов размытости и правой
границе
коэффициентов размытости и правой
границе
![]() .
Для генерации коэффициентов размытости
.
Для генерации коэффициентов размытости
![]() воспользуемся датчиками случайных
величин известных законов распределения,
например (рис. 3.6):
воспользуемся датчиками случайных
величин известных законов распределения,
например (рис. 3.6):
Нормальный закон
 .
.
Равномерный закон
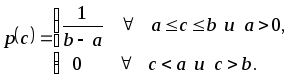
Показательный


Рис. 3.6. Графики
плотностей вероятности в диапазоне
![]() .
Кривая 1 соответствует нормальному
закону распределения при
.
Кривая 1 соответствует нормальному
закону распределения при
![]() ,
,
![]() ;
кривая 2 – равномерному закону при
;
кривая 2 – равномерному закону при
![]() ,
,
![]() ;
кривая 3 и 4 – показательным законам для
;
кривая 3 и 4 – показательным законам для
![]() ,
,
![]() при
при
![]() .
.
Воспользуемся результатами раздела 2.5. и сформируем датчики случайных величин введённых законов распределения:
- нормальный закон
 ,
где параметр распределения
,
где параметр распределения
![]() ;
;
- равномерный закон
распределения
![]() на интервале
на интервале
![]() ;
;
- показательный
закон распределения
![]() на интервале
на интервале
![]() .
.
Здесь
![]() случайная величина с равномерным законом
распределения.
случайная величина с равномерным законом
распределения.
При использовании
датчика случайных значений коэффициентов
размытости с нормальным законом
распределения задача оптимизации
непараметрической оценки регрессии
сводится к нахождению оптимальных
значений математического ожидания
коэффициента размытости
![]() и его среднеквадратического отклонения
и его среднеквадратического отклонения
![]() .
Для датчика с равномерным законом
необходимо определить оптимальную
длину интервала
.
Для датчика с равномерным законом
необходимо определить оптимальную
длину интервала
![]() ,
(
,
(![]() и
и
![]() )
и его центр, а при использовании датчика
с показательным законом необходимо
эффективно оценить правую границу
)
и его центр, а при использовании датчика
с показательным законом необходимо
эффективно оценить правую границу
![]() и наилучшую степень
и наилучшую степень
![]() .
.
При использовании
датчика случайных чисел, например, с
показательным законом распределения
при
![]() непараметрическая оценка регрессии
имеет вид
непараметрическая оценка регрессии
имеет вид
 ,
(3.17)
,
(3.17)
где оптимальный
набор параметров
![]() определяется из эмпирической оценки
среднеквадратического отклонения
определяется из эмпирической оценки
среднеквадратического отклонения
 .
.
Пример применения непараметрической оценки регрессии при восстановлении стохастической зависимости. Для иллюстрации эффективности непараметрической оценки регрессии (3.4) в задачах восстановления стохастических зависимостей (3.1) проведён вычислительный эксперимент с использованием функции
![]() .
(3.18)
.
(3.18)
Методика формирования исходных данных:
1. Случайная величина
![]() генерировалась в диапазоне
генерировалась в диапазоне
![]() с равномерным законом распределения.
с равномерным законом распределения.
2. Значения функции
![]() получались путём подстановки
получались путём подстановки
![]() в полином (3.18)
в полином (3.18)
![]() .
.
3. Полученная
выборка
![]() зашумлялась, накладывая на значения
восстанавливаемой функции аддитивную
относительную помеху
зашумлялась, накладывая на значения
восстанавливаемой функции аддитивную
относительную помеху
![]() ,
,
где
![]() - уровень шума,
- уровень шума,
![]() - случайная величина с равномерным
законом распределения.
- случайная величина с равномерным
законом распределения.
Используя
непараметрическую оценку регрессии
(3.4) и метод скользящего экзамена при её
оптимизации по данным
![]() восстанавливалась зависимость
восстанавливалась зависимость
![]() рис. 3.7.
рис. 3.7.

Рис. 3.7. Иллюстрация
восстановления стохастической зависимости
(3.1) с помощью непараметрической
регрессии(3.4) при
![]() ,
,
![]() .
.
