5. Средне-квадратичная скорость молекул газа.

Так как , то, следовательно, …(11.12)

где – кинетическая энергия всех молекул газа.

Массу газа можно выразить как , тогда (12.12) запишется как ; для одного моля газа, то есть m = M, а V = V_

 , отсюда

Так как молярную массу можно выразить через массу одной молекулы m₀ и число Авогадро - , то квадратичную скорость можно представить как

где - постоянная Больцмана.

При комнатной температуре молекулы кислорода, например, имеют среднеквадратическую скорость 480м/с, водорода – 1900м/с.

6. Средняя кинетическая энергия поступательного движения молекул газа.

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа – она пропорциональна термодина-мической температуре и зависит только от нее, то есть температура тела есть количественная мера энергии движения молекул, из которых состоит это тело. Кроме того, связи между абсолютной температурой и средней кинетической энергией показывает, что при одинаковой температуре средние кинетические энергии молекул всех газов одинаковы, несмотря на различие масс молекул разных газов.

Кинетическая энергия газа состоящего из молекул, равна

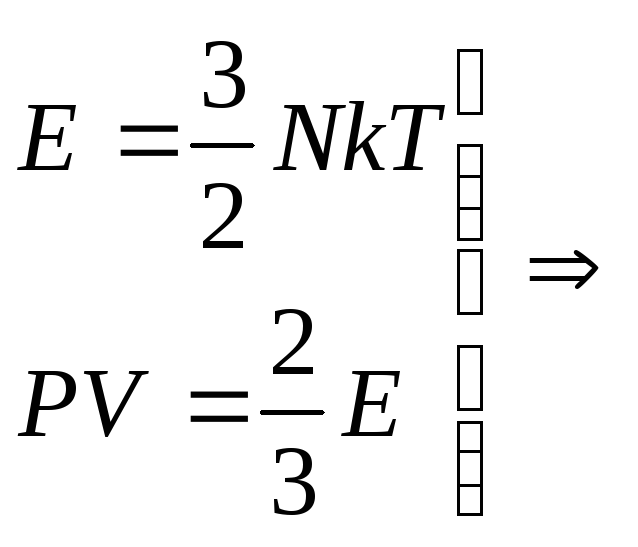
, то есть , отсюда , где - концентрация молекул, тогда – получили уравнение состояния идеального газа. Из этих выражений видно, что если то <E₀> = 0, то есть прекращается поступательное движение молекул идеального газа, а, , его давление равно нулю.

Не следует думать, что при абсолютном нуле температуры, прекращается всякое движение частиц вещества. Даже если все молекулы газа остановятся, то внутри них будут двигаться электроны, будут участвовать в движении протоны и нейтроны ядер.

Абсолютный ноль температур означает для реальной системы не отсутствие движения, но такое состояние тела, при котором дальнейшее уменьшение интенсивности этого движения за счет отдачи его энергии окружающим телам невозможно. Следовательно, при абсолютном нуле система находится в состоянии с наименьшей возможной энергией. Характер этого состояния зависит от конкретных свойств составляющих систему частиц.

7. Любая молекулярная система состоит из большого числа составных частиц (идеальный газ). Эти частицы беспорядочно движутся. Скорости каждой частицы в произвольный момент времени неизвестны. Но, оказываются разные скорости различных частиц встречаются с разными вероятностями. В этом можно убедится на опыте Штерна (1888 – 1970):

	Раскаленная током нить расположена на оси двух имеющих общую ось цилиндров. Нить покрыта серебром., атомы которого
	испаряясь, покидают нить и по радиусу разлетаются в разные
	стороны. Во внутреннем цилиндре сделана узкая щель. Только
	те атомы, которые попали в щель, достигают внутренней

поверхности внешнего цилиндра, они создают изображение щели, которое можно увидеть, если через некоторое время развернуть внутреннюю поверхность большого цилиндра. Если прибор привести во вращение вокруг общей оси, то атомы серебра, прошедшие сквозь щель, будут оседать не прямо напротив него, а с некоторым смещением. Если бы всех молекул серебра была одинакова, то и это смещение было бы одинаковым, но опыт показал распределение по скоростям.

	Существует некая скорость
	около которой расположе-
	ны наиболее населенные
	интервалы, она называется
	наиболее вероятной скоро-
	стью Uв и ей соответству-
	ет максимум на рисунке.

Чем больше скорость частиц отличается от U_в, тем меньше число таких частиц. С увеличением возрастает наиболее вероятная скорость, больше появится быстрых частиц, вся кривая сместится вправо. Однако площадь под кривой остается постоянной (так как постоянно число частиц), кривая растягивается. Сама кривая называется: распределение Максвелла молекул по скоростям.

Применив методы теории вероятностей, Максвелл нашел функцию распределения по скоростям f (1)

Значение наиболее вероятной скорости можно найти, продифференцировав (1):

(2)

Средняя скорость молекул определяется по формуле:

(3)

Таким образом, состояние газа характеризуется следующими скоростями:

1) наиболее вероятная

2) средняя

3) Средняя квадратичная

Исходя из распределения молекул по скоростям можно определить функцию распределения молекул по энергиям теплового движения

(4)

Тогда средняя кинетическая энергия :

7