2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации и эмпирического корреляционного отношения

Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации и эмпирическое корреляционное отношение .

Эмпирический коэффициент детерминации оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формуле

, (9)

где – общая дисперсия признака Y,

– межгрупповая (факторная) дисперсия признака Y.

Значения показателя изменяются в пределах . При отсутствии корреляционной связи между признаками Х и Y имеет место равенство =0, а при наличии функциональной связи между ними - равенство =1.

Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле

, (10)

где y_i – индивидуальные значения результативного признака;

– общая средняя значений результативного признака;

n – число единиц совокупности.

Общая средняя вычисляется как средняя арифметическая простая по всем единицам совокупности:

(11)

или как средняя взвешенная по частоте групп интервального ряда:

(12)

Для вычисления удобно использовать формулу (11), т.к. в табл. 7 (графы 3 и 4 итоговой строки) имеются значения числителя и знаменателя формулы.

Расчет по формуле (11):

Для расчета общей дисперсии применяется вспомогательная таблица 11.

Таблица 11

Вспомогательная таблица для расчета общей дисперсии.

Номер банка по п/п	Прибыль, млн.руб.	Yi - Y ср.	(Yi - Y ср.)^2	Yi^2
1	110	-75,970	5 771,441	12100
2	538	352,030	123 925,121	289444
3	68	-117,970	13 916,921	4624
4	213	27,030	730,621	45369
5	146	-39,970	1 597,601	21316
6	70	-115,970	13 449,041	4900
7	111	-74,970	5 620,501	12321
8	153	-32,970	1 087,021	23409
9	215	29,030	842,741	46225
10	224	38,030	1 446,281	50176
11	203	17,030	290,021	41209
12	348	162,030	26 253,721	121104
13	64	-121,970	14 876,681	4096
14	240	54,030	2 919,241	57600
15	153	-32,970	1 087,021	23409
16	134	-51,970	2 700,881	17956
17	121	-64,970	4 221,101	14641
18	94	-91,970	8 458,481	8836
19	105	-80,970	6 556,141	11025
20	93	-92,970	8 643,421	8649
21	329	143,030	20 457,581	108241
22	269	83,030	6 893,981	72361
23	451	265,030	70 240,901	203401
24	139	-46,970	2 206,181	19321
25	62	-123,970	15 368,561	3844
26	441	255,030	65 040,301	194481
27	237	51,030	2 604,061	56169
28	282	96,030	9 221,761	79524
29	91	-94,970	9 019,301	8281
30	166	-19,970	398,801	27556
31	165	-20,970	439,741	27225
32	112	-73,970	5 471,561	12544
33	77	-108,970	11 874,461	5929
34	204	18,030	325,081	41616
35	78	-107,970	11 657,521	6084
36	189	3,030	9,181	35721
Итого	6695	0,080	475 622,972	1720707

Расчет общей дисперсии по формуле (10):

Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних от общей средней . Показатель вычисляется по формуле

, (13)

где –групповые средние,

– общая средняя,

–число единиц в j-ой группе,

k – число групп.

Для расчета межгрупповой дисперсии строится вспомогательная таблица 12 При этом используются групповые средние значения из табл. 7 (графа 5).

Таблица 12

Вспомогательная таблица для расчета межгрупповой дисперсии.

Группы банков по объему работающих активов,Xi	Число банков,Fi	Среднее значение Yj в группе,	Yj ср - Yi ср.	(Yj ср - Yi ср.)^2*Fi
4493,00 - 8816,40	7	144,57	-41,40	11998,18
8816,40 - 13139,80	10	146,20	-39,77	15818,2966
13139,80 - 17463,20	9	187,44	1,47	19,50694444
17463,20 - 21786,60	5	213,20	27,23	3706,759414
21786,60 - 26110,00	5	293,60	107,63	57918,69275
Итого	36			89461,43571

Расчет межгрупповой дисперсии по формуле (13):

Расчет эмпирического коэффициента детерминации по формуле (9):

^{или 18,8%}

Вывод. 18,8% вариации суммы прибыли банков обусловлено вариацией объема работающих активов, а 81,2% – влиянием прочих неучтенных факторов.

Эмпирическое корреляционное отношение оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле

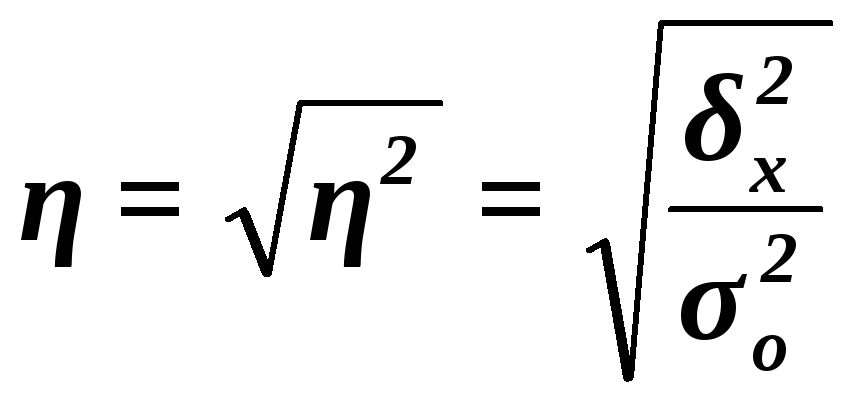(14)

Значение показателя изменяются в пределах . Чем ближе значение к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе служит шкала Чэддока (табл. 14):

Таблица 13

Шкала Чэддока

	0,1 – 0,3	0,3 – 0,5	0,5 – 0,7	0,7 – 0,9	0,9 – 0,99
Характеристика силы связи	Слабая	Умеренная	Заметная	Тесная	Весьма тесная

Расчет эмпирического корреляционного отношения по формуле (14):

^{или 43,4%}

Вывод. Согласно шкале Чэддока связь между объемом работающих активов и суммой прибыли банков является умеренной.