Лабораторная работа № 5 решение интегральных уравнений
Дано интегральное
уравнение Фредгольма
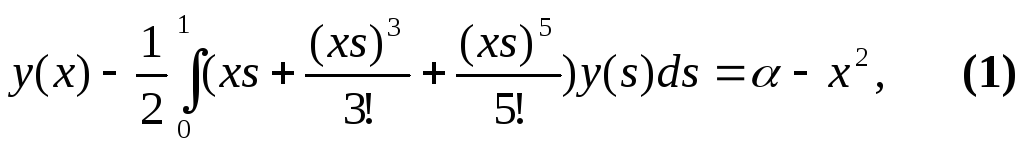
где
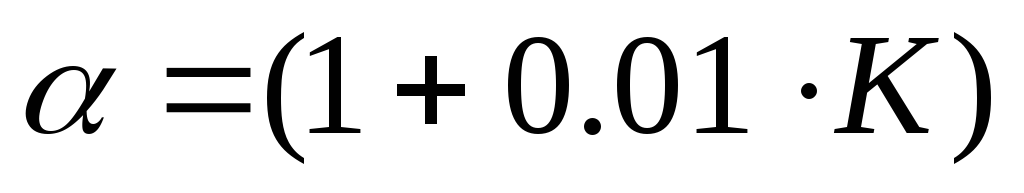 ,
,
 – номер варианта.
– номер варианта.
Задание 1.
Решить
уравнение (1) методом последовательных
приближений. Заменить решение отрезком
ряда
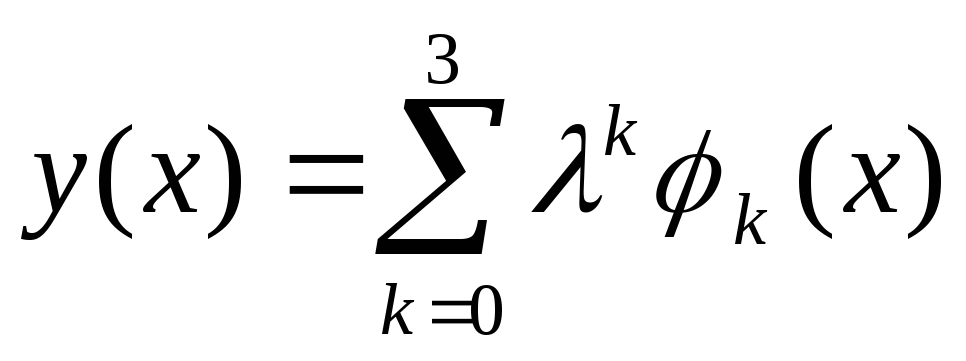 .
.
Задание
2.
Решить
уравнение (1) методом конечных сумм.
Использовать квадратурную формулу
Симпсона в обобщенном виде. Разбить
отрезок на 4 равные части:
 .
.
Задание
3.
Решить
уравнение (1) методом вырожденных ядер.
Решение искать в виде

Задание
4.
Решить
уравнение (1) методом коллокации. Искать
решение в виде
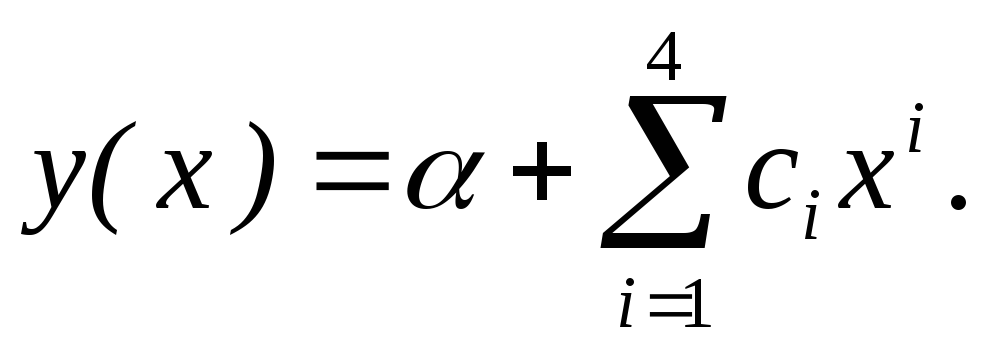 Взять в качестве точек коллокации точки
Взять в качестве точек коллокации точки
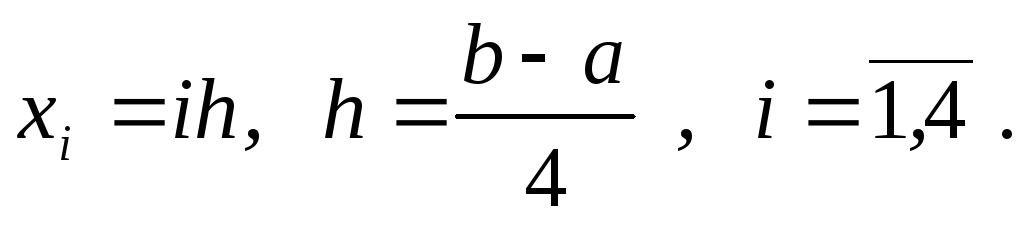
Задание
5.
Решить
уравнение (1) методом моментов. Искать
решение в виде
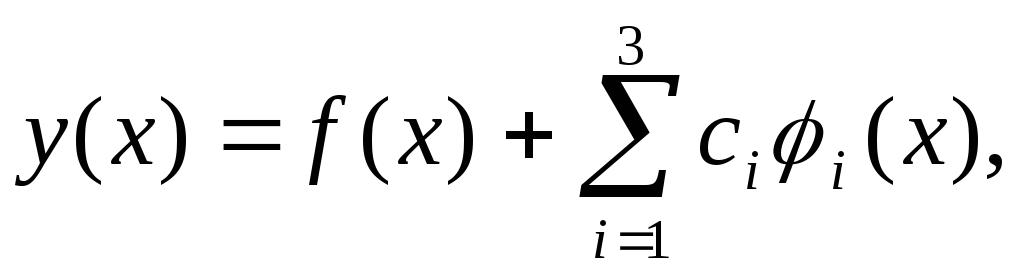 где
где
 .
.
Задание
6.
Решить
уравнение (1) методом наименьших квадратов.
Искать решение в виде
 .
.
Вопросы по теме
-
Уравнения
какого вида называются интегральными
уравнениями (ИУ)?
-
Какое
ИУ называется линейным?
-
ИУ
Фредгольма.
-
ИУ
Вольтерра.
-
Однородное
ИУ. Собственные значения, собственные
функции.
-
Теорема
Фредгольма.
-
Симметрические
ядра. Их свойства.
-
Основные
задачи, возникающие в теории ИУ.
-
Метод
последовательных приближений.
-
Метод
конечных сумм.
-
Выбор
квадратурной формулы в методе конечных
сумм.
-
Понятие
о вырожденном ядре.
-
Метод
вырожденных ядер.
-
Метод
коллокации.
-
Метод
наименьших квадратов.
-
Метод
моментов.

