
- •Занятие 1 Основные элементарные функции
- •Задания для самостоятельного решения
- •Занятие 2 Числовая последовательность. Бесконечно малые и бесконечно большие величины. Предел последовательности
- •Действия над последовательностями
- •Операции над пределами последовательностей
- •Аудиторные задания
- •Домашние задания
- •Занятие 3
- •Предел функции.
- •Раскрытие неопределённостей вида ,
- •Чтобы раскрыть неопределённость, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.
- •Аудиторные задания
- •Домашние задания Найти пределы:
- •Дополнительные задания
- •Занятие 4 Замечательные пределы
- •Следствия
- •Аудиторное занятие
- •Домашние задания
- •Примерный вариант решения индивидуального домашнего задания «Вычисление пределов»
- •Занятие 5 Вычисление пределов при использовании эквивалентностей
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 6 Обзорное занятие
- •Занятие 7 Непрерывность функции
- •Аудиторные задания
- •Домашние задания
- •Контрольные вопросы Последовательности и непрерывные функции
- •Функция, её простейшие свойства
- •Вариант 1
- •Литература
- •Содержание
- •Занятие 4
- •Решение идз
- •Занятие 7
Занятие 4 Замечательные пределы
Цели
Знать:
-
Замечательные пределы и их следствия.
Уметь:
-
Вычислять пределы, используя замечательные пределы.
Первый замечательный предел
![]() (29).
(29).
Следствия
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Второй замечательный предел
![]() ,
,
![]() , (30)
, (30)
где е![]() — число Эйлера.
— число Эйлера.
Следствия
![]() ;
;
![]() ,
,
![]() ;
; ![]() ;
;
![]() ;
; ![]() ,
(а=const).
,
(а=const).
Постановка
задачи. Найти
![]() .
.
План решения.
Для того чтобы найти данный предел
следует вычислить
![]() и
и
![]() ;
;
1) если
существуют конечные пределы
![]() ;
;
![]() ,
то
,
то
![]() ;
;
2) если
![]() и
и
![]() ,
то С находится с помощью формул:
,
то С находится с помощью формул:


3) если
![]() и
и
![]() ,
то положив
,
то положив
![]() ,
где
,
где
![]() при
при
![]() ,
получим:
,
получим:
 =
=![]() .
.
№14. Найти
пределы:1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)![]() ;
;
6)
![]() ;
7)
;
7)
![]() .
.
► 1)
![]() .
Воспользуемся первым замечательным
пределом:
.
Воспользуемся первым замечательным
пределом:
![]() ;
;
2)
![]() .
Вычислим пределы двух функций:
.
Вычислим пределы двух функций:
 ,
,
т.к. пределы
существуют и они конечны, то
![]() =32;
=32;
3)
![]() .
Вычислим пределы двух функций:
.
Вычислим пределы двух функций:
 ,
,
тогда для нахождения исходного предельного выражения воспользуемся формулой:

т.е. имеем
![]() ,
следовательно
,
следовательно
![]() =0;
=0;
4)
![]() .
Вычислим пределы двух функций:
.
Вычислим пределы двух функций:

т.е. имеем
неопределенность
![]() .
Для раскрытия данной неопределенности
воспользуемся вторым замечательным
пределом, т.е.:
.
Для раскрытия данной неопределенности
воспользуемся вторым замечательным
пределом, т.е.:
![]() =
=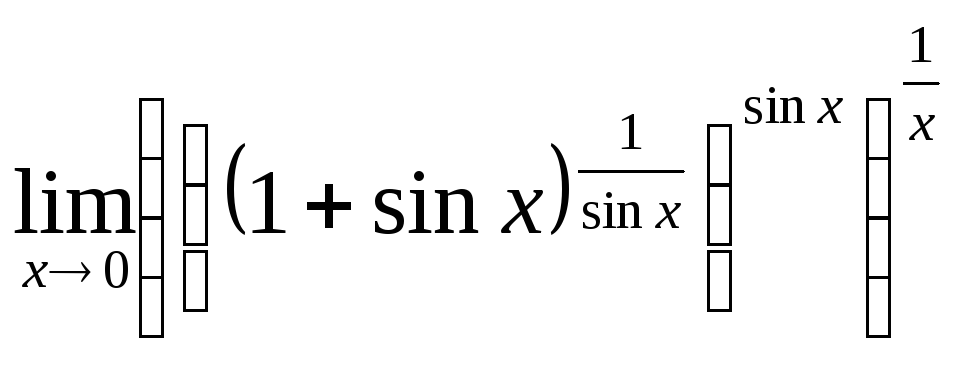 =
=![]() ;
;
5)
![]() .
Введем замену:
.
Введем замену:

Тогда,
![]() =
=
=![]() =
= ;
;
6)
![]() .
Введем замену:
.
Введем замену:

Тогда,
![]() =
=![]() =
=![]() =
=
=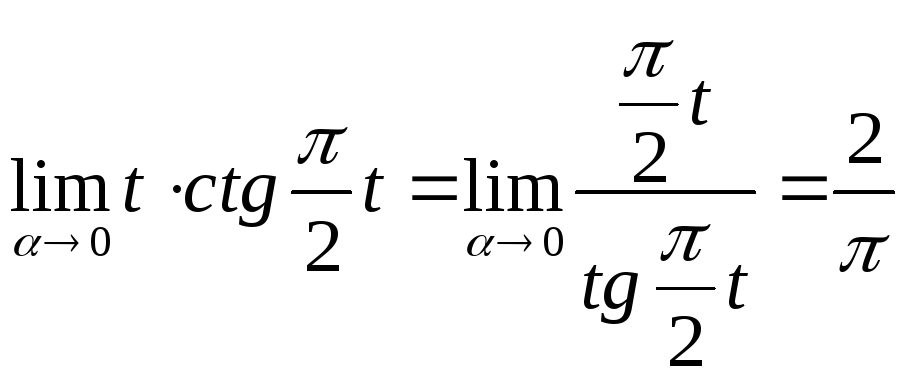 ;
;
7)
![]() .
Найдя пределы двух функций, имеем
неопреденность:
.
Найдя пределы двух функций, имеем
неопреденность:
![]() .
.
Тогда,
![]() =
=![]() =
=![]() =
=
= =
=![]() .
◄
.
◄
Аудиторное занятие
Найти пределы:
№123.
![]() .
Ответ:
.
Ответ:
![]() .
.
№124.
![]() .
Ответ:
.
Ответ:
![]() .
.
№125.
![]() .
Ответ:
0.
.
Ответ:
0.
№126.
![]() .
Ответ:
.
Ответ:
![]() .
.
№127.
![]() .
Ответ:
.
Ответ:
![]() .
.
№128.
![]() .
Ответ:
.
Ответ:
![]() .
.
№129.
![]() .
Ответ: 12.
.
Ответ: 12.
№130.
![]() .
Ответ:
.
Ответ:
![]() .
.
№131.
![]() .
Ответ:
.
Ответ:
![]() .
.
№132.
![]() .
Ответ: 1.
.
Ответ: 1.
№133.
![]() .
Ответ:
1.
.
Ответ:
1.
№134.
![]() .
Ответ:
.
Ответ:
![]() .
.
№135.
![]() .
Ответ:
.
Ответ:
![]() .
.
Домашние задания
Найти пределы:
№136.
![]() .
Ответ:
.
Ответ:
![]() .
.
№137.
 .
Ответ:
.
Ответ:
![]() .
.
№138.
 .
Ответ:
.
Ответ:
![]() .
.
№139.
![]() .
Ответ:
.
Ответ:
![]() .
.
№140.
![]() .
Ответ:
.
Ответ:
![]() .
.
№141.
 .
Ответ:
.
Ответ:
![]() .
.
№142.
![]() .
Ответ:
.
Ответ:
![]() .
.
№143.
![]() .
Ответ: –1.
.
Ответ: –1.
№144.
![]() .
Ответ:
.
Ответ:![]() .
.
№145.
![]() .
Ответ:
.
Ответ:
![]() .
.
№146.
![]() .
Ответ: е.
.
Ответ: е.
№147.
![]() .
Ответ:
.
Ответ:
![]() .
.
№148.
![]() .
Ответ: е.
.
Ответ: е.
Дополнительные задания
Найти пределы:
№149.
![]() .
Ответ: 4.
.
Ответ: 4.
№150.
![]() .
Ответ:
1.
.
Ответ:
1.
№151.
![]() .
Ответ:
.
Ответ:
![]() .
.
№152.
![]() .
Ответ:
.
Ответ:
![]() .
.
№153.
 .
Ответ:
.
Ответ:
![]() .
.
№154.
![]() .
Ответ: е.
.
Ответ: е.
№155.
![]() .
Ответ:
.
Ответ:
![]() .
.
№156.
![]() .
Ответ:
.
Ответ:
![]() .
.
№157.
![]() .
Ответ:
.
Ответ:
![]() .
.
№158.
![]() .
Ответ:
.
Ответ:
![]() .
.
№159.
![]() .
Ответ:
.
Ответ:
![]() .
.
№160.
![]() .
Ответ: 1.
.
Ответ: 1.
