Чтобы раскрыть неопределённость, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Введение в анализ.doc

Скачиваний:

Добавлен:

09.12.2018

Размер:

2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 135 6 7 8 9 10 11 12 13 > Следующая >>>

Для того чтобы разрешить неопределённость вида, до вычисления предела средствами алгебры в числителе и знаменателе выделяем множитель и сокращаем на него, т.к. .
Чтобы раскрыть неопределённость, в которой числитель или знаменатель содержит иррациональность, следует соответствующим образом избавиться от иррациональности.

Неопределённость вида

Если числитель и знаменатель, сложные степенные функции: необходимо вынести за скобку в числителе и знаменателе дроби неизвестное с наибольшим показателем степени среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.

Частный случай: предел рационального выражения вида

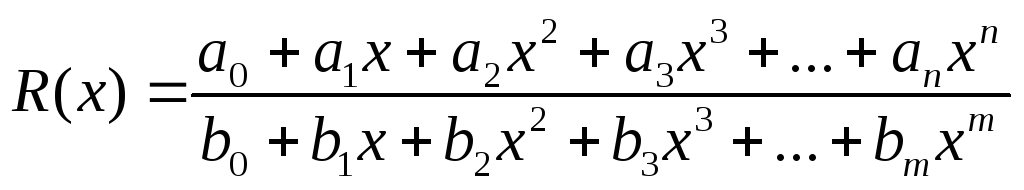при будем рассматривать как предел частного двух многочленов, который равен:

Если числитель и знаменатель, сложные показательные функции: за скобку вынести наиболее быстро возрастающее слагаемое среди всех слагаемых дроби; после сокращения дроби неопределённость устраняется.

№10. Найти пределы: 1) ;

2) ; 3) .

► 1) =, для раскрытия данной неопределенности средствами алгебры разложим числитель и знаменатель на множители:

сократим множитель (х – 3) имеем:

2) . Данное предельное выражение содержит иррациональность в числителе, следовательно, домножим дробь на сопряженное выражение, т.е. на , тогда:

В числителе последнего выражения получилась формула — разность квадратов, таким образом:

;

3) , для раскрытия данной неопределенности сделаем замену:

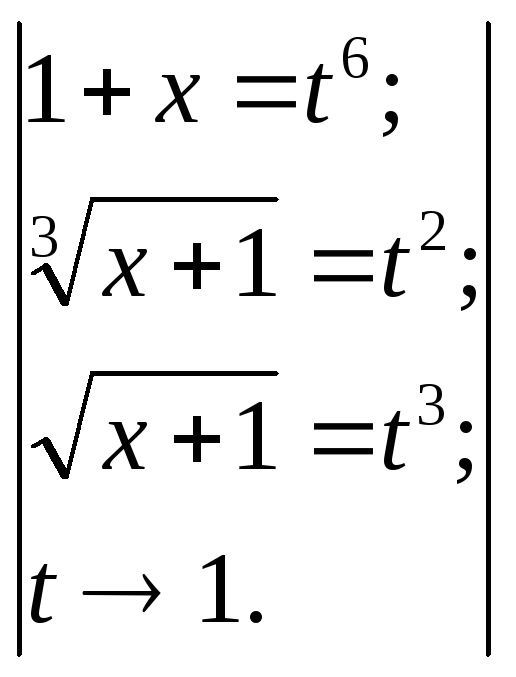
тогда исходное пределное выражение имеетвид:

которое раскрывается по известным правилам, т.е.:

==. ◄

№11. Найти пределы: 1) ; 2) ;

3) ; 4) .

► 1) , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х², тогда:

2) , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на х³, тогда:

;

3) , для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n⁴, тогда:

==;

4) =, для раскрытия данной неопределенности разделим почленно числитель и знаменатель на n, тогда:

==0. ◄

№12. Найти пределы: 1) ;

2) ; 3) .

► Данные предельные соотношения можно рссмотреть, как частное двух многочленов, т.е:

1) ==2;

2) ;

3) .◄

Постановка задачи. Найти .

План решения. Для того чтобы найти вычисляем f (х₀), если в результате вычислений получилась одна из неопределённостей , или др., то данные неопределённости раскрываются путём преобразования и сведения их к неопределённости или.