
- •Занятие 1 Прямоугольная система координат
- •Занятие 2 Различные виды уравнения прямой на плоскости Цели
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Прямая на плоскости»
- •Занятие 3 Кривые второго порядка Цели
- •1. Эллипс
- •2. Окружность
- •3. Гипербола
- •4. Парабола
- •Различные виды парабол
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 4 Уравнение кривых второго порядка с осями симметрии, параллельными координатным осям. Параметрические уравнения линий
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 5 Полярная система координат
- •Аудиторное задание
- •Задание и общие указания
- •Инструкция к работе
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Кривые второго порядка»
- •Задание 5. Построить кривую, заданную параметрическими уравнениями:
- •Контрольные вопросы
- •Кривые второго порядка
- •Параметрические уравнения
- •Полярная система координат
- •Примерный вариант контрольной работы Вариант 1
- •Литература
- •Содержание
Аудиторные задания
Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой:
№84. 9х2+4у2 – 54х – 32у+109=0.
Ответ:
![]() .
.
№85. х2 – у2 – 4х+2у+7=0.
Ответ:
![]() .
.
№86. х2 – 9у2+2х – 36у – 44=0.
Ответ:
![]() .
.
№87. у=х2+4х+5.
Ответ: (х+2)2=у – 1.
Построить линию, заданную параметрическими уравнениями:
№88.
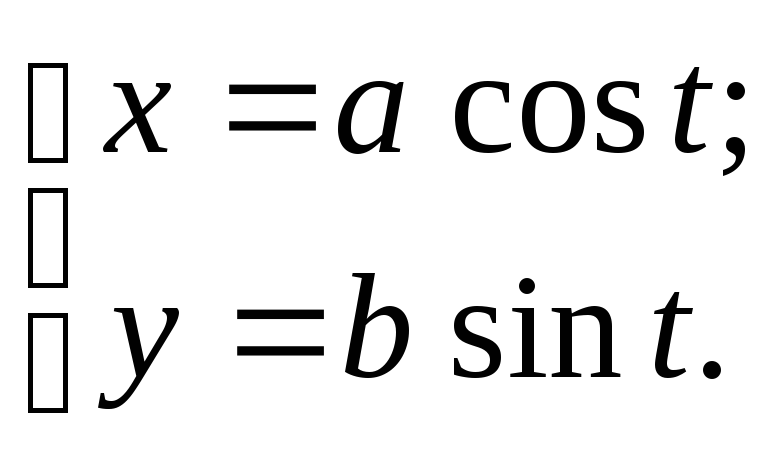 Ответ:
эллипс.
Ответ:
эллипс.
№89.
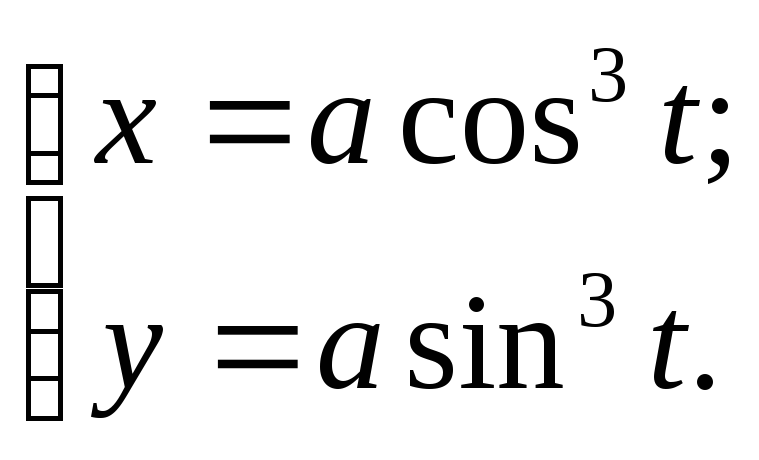 Ответ: астроида.
Ответ: астроида.
Домашние задания
Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой:
№90. 4х2+9у2 – 8х – 36у+4=0.
Ответ:
![]() .
.
№91. х2 – 9у2+2х+36у – 44=0.
Ответ:
![]() .
.
№92. у=х2 – 5х+7.
Ответ:
![]() .
.
№93. х2+4у2 – 4х – 8у+8=0. Ответ: О(2; 1).
№94. х2+4у2+8у+5=0. Ответ: мнимый эллипс.
№95. х2 – у2 – 6х+10=0.
Ответ: у2 – (х – 3)2=1.
№96. х2 – 6х+8=0.
Ответ: х=2; х=4.
№97. х2+2х+5=0. Ответ: мнимые прямые.
Построить линию, заданную параметрическими уравнениями:
№98.
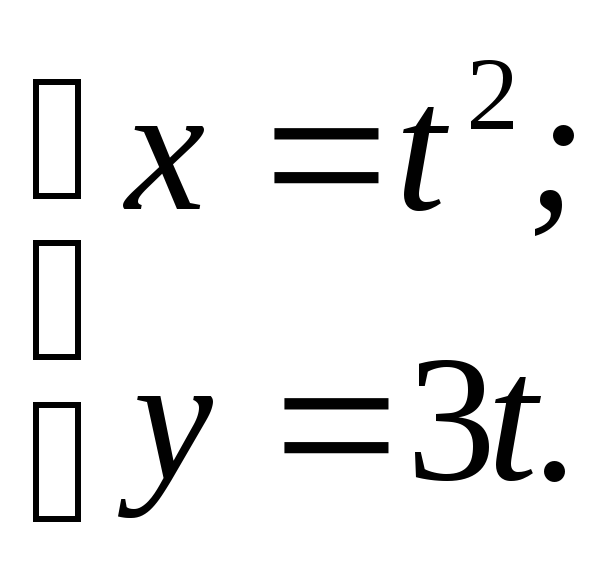 Ответ: парабола
у2=9х.
Ответ: парабола
у2=9х.
№99.
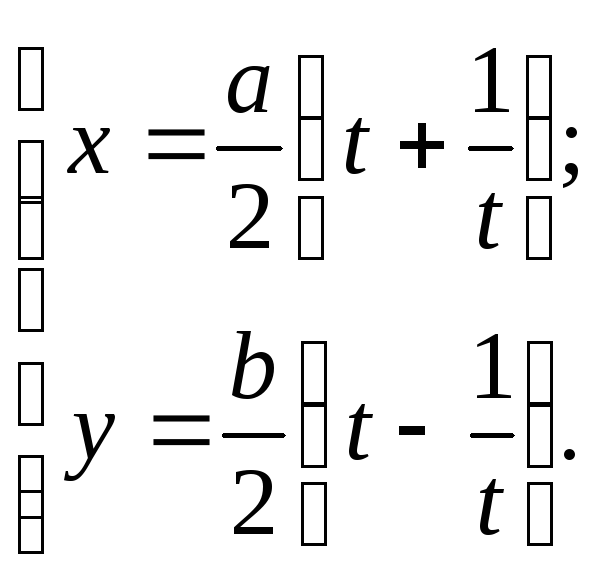 Ответ: гипербола
Ответ: гипербола
![]() .
.
№100.
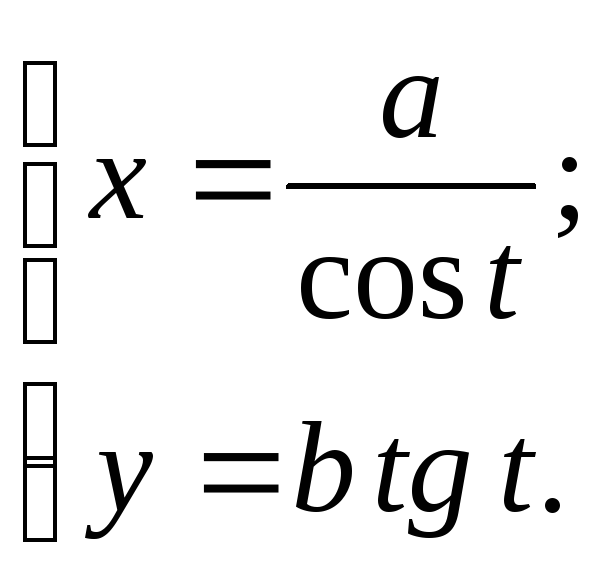 Ответ: гипербола.
Ответ: гипербола.
№101.
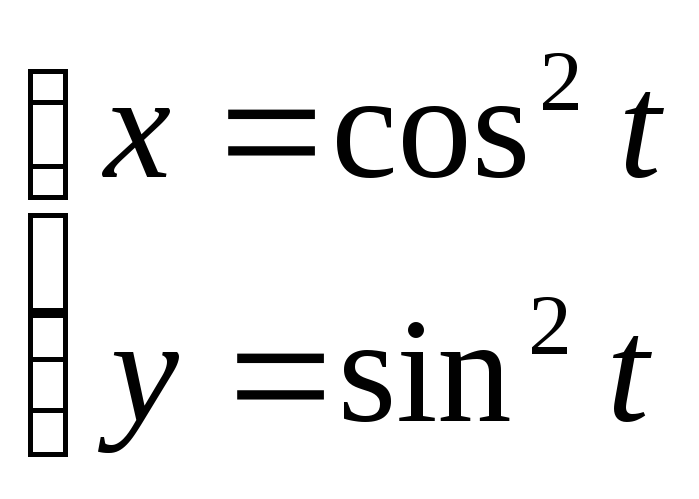
Ответ: отрезок прямой, соединяющий точки А(1; 0) и В(0; 1).
Дополнительные задания
Преобразовать к каноническому виду уравнения, построить кривые, определить все характеристики полученной кривой:
№102. 36х2+36у2 – 36х – 24у – 23=0.
Ответ:
![]() .
.
№103.
![]() .
.
Ответ:
![]() .
.
№104. 16х2+25у2 – 32х+50у – 359=0.
Ответ:
![]() .
.
№105. у=4х2+8х+7. Ответ: 4(х+1)2=у – 3.
Построить линию, заданную параметрическими уравнениями:
№106.
![]()
Ответ: луч, направленный по биссектрисе первого координатного угла.
№107.
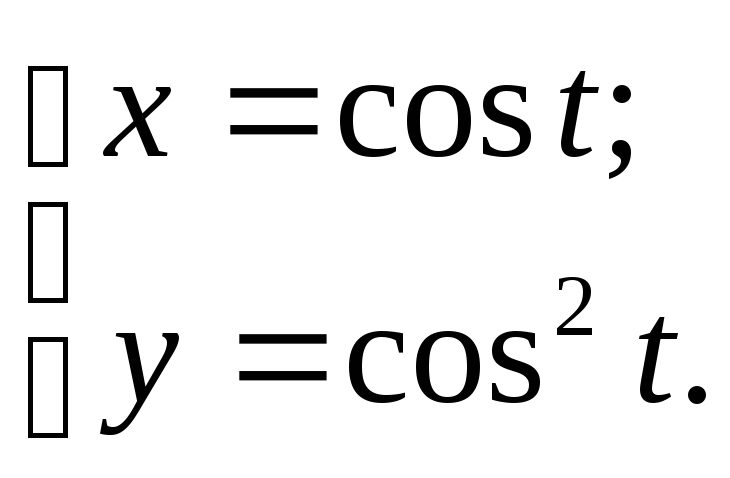 Ответ:
дуга параболы.
Ответ:
дуга параболы.
№108.
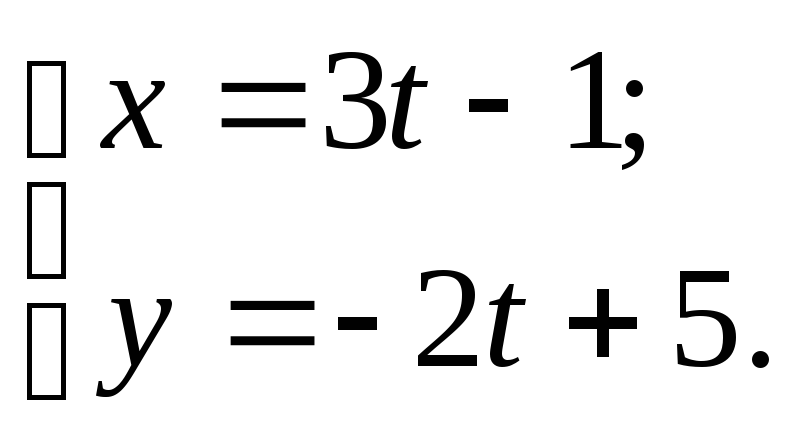
№109.
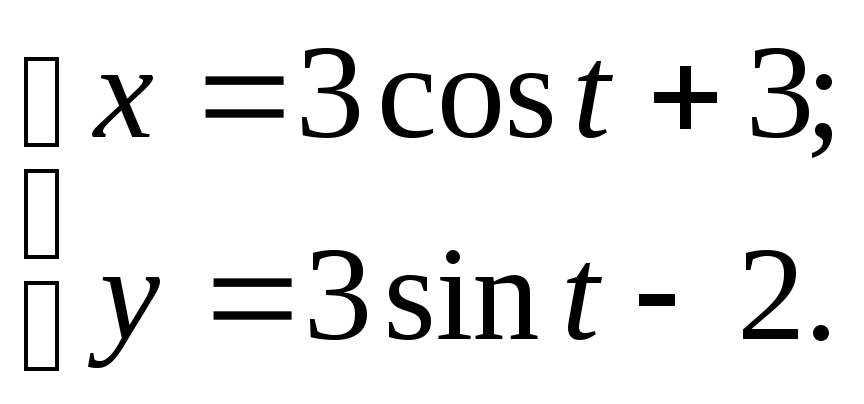
№110.
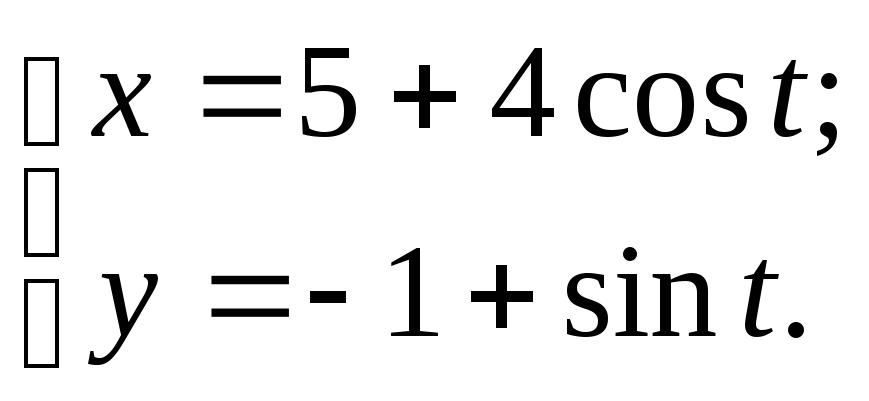
№111.
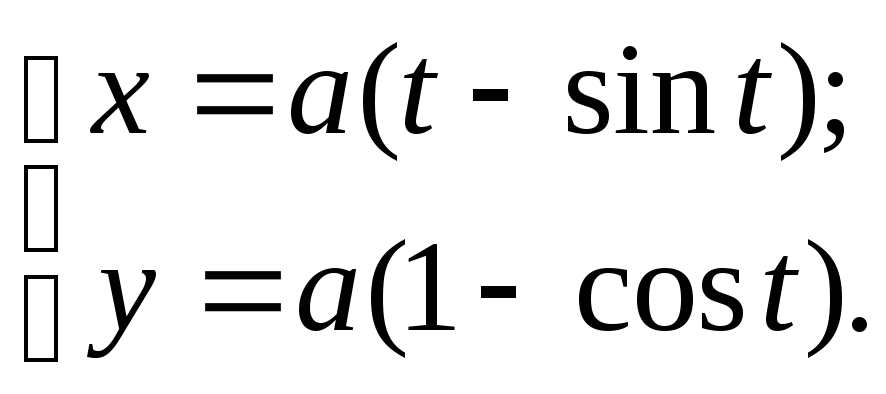
Занятие 5 Полярная система координат
Цели
Знать:
-
Связь между полярной и прямоугольной системой координат;
-
уравнения основных линий в полярной системе координат.
Уметь:
-
Схематически строить линию в полярной системе координат.
Cвязь между полярными и прямоугольными координатами точки устанавливается формулами:
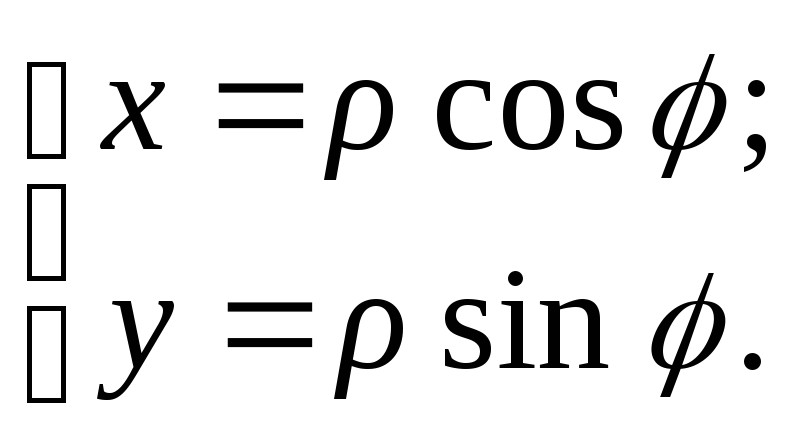 (39)
(39)
при этом полюс полярной системы координат О совмещен с началом координат системы XOY, а полярная ось — с положительной полуосью ОX (рис.14).

рис.14
Переход от декартовых координат к полярным координатам:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() . (40)
. (40)
Аудиторное задание
Выполнить лабораторную работу «Построение линий в полярной системе координат».
Цель работы: приобретение навыков построения линий по уравнению в полярной системе координат.
Задание и общие указания
-
Все вычисления оформляются на расчетном листе;
-
кривые строятся на миллиметровой бумаге;
-
при расчётах используется МК.
Инструкция к работе
№1.
Построить точки в полярной системе
координат:
![]()
► Отрицательные
углы
![]() отсчитываются по часовой стрелке,
отрицательные значения
отсчитываются по часовой стрелке,
отрицательные значения
![]() откладываются не на луче, наклонённом
к полярной оси под углом
откладываются не на луче, наклонённом
к полярной оси под углом
![]() ,
а на его продолжении за полюс (т.е. на
луче, образующем с полярной осью угол
,
а на его продолжении за полюс (т.е. на
луче, образующем с полярной осью угол
![]() )
(рис.15). ◄
)
(рис.15). ◄
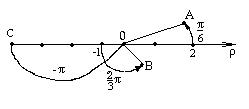
рис.15
№2.
Построить линии: а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
Провести краткое исследование формы кривой по уравнению: 1) симметрия кривой;
2) область существования кривой;
3)
для построения линий в полярных
координатах составить таблицу значений
![]() и
и
![]() ,где
,где
![]() ,
выбрав шаг
,
выбрав шаг
![]() (n
— коэффициент перед
(n
— коэффициент перед
![]() в уравнении линии).
в уравнении линии).
► а)
![]() — данная линия окружность.
— данная линия окружность.
1)
Линия симметрична относительно прямой
![]() ;
;
2)
![]() ,
достаточно рассмотреть
,
достаточно рассмотреть
![]() ;
;
3)
Составим таблицу с шагом
![]() :
:
|
|
0 |
|
|
|
|
|
|
|
0 |
2 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
0 |
–2 |
– |
–4 |
– |
–2 |
0 |
По данным таблицы построим искомую линию (рис.16).
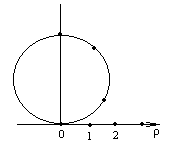
рис.16
б)
![]() — данная линия кардиоида.
— данная линия кардиоида.
1) линия симметрична относительно полярной оси;
2)
![]() ,
достаточно
,
достаточно
![]() в виду симметрии кривой;
в виду симметрии кривой;
3)
составим таблицу с шагом
![]() :
:
|
|
0 |
|
|
|
|
|
|
|
|
2 |
1,86 |
1,5 |
1 |
0,5 |
0,14 |
0 |
По данным таблицы построим искомую линию (рис.17).
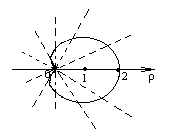
рис.17
в)
![]() или
или
![]() — данная линия лемниската Бернулли.
— данная линия лемниската Бернулли.
1) линия симметрична относительно полюса О;
2)
![]() ;
;
![]() ;
;
3)
составим таблицу с шагом
![]() :
:
|
|
0 |
|
|
|
|
|
|
… |
|
|
0 |
0,7 |
0,9 |
1 |
0,9 |
0,7 |
0 |
… |
|
|
… |
|
|
|
|
|
|
|
|
|
… |
0 |
0,7 |
0,9 |
1 |
0,9 |
0,7 |
0 |
По данным таблицы построим искомую линию (рис.18).
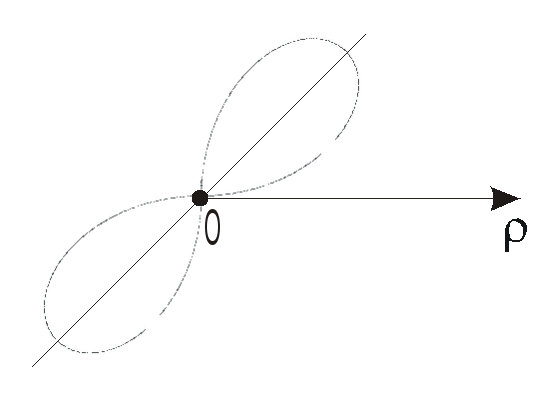
рис.18◄
№3. Записать уравнения линий, заданных в п.2, в декартовой системе координат.
► Используя формулы перехода от полярной системы координат к декартовой (40) имеем:
а)
![]() ;
;
![]() ;
;
х2+у2=4у;
х2+(у – 2)2=4 — уравнение смещённой окружности.
б)
![]() ;
;
![]() ;
;
![]() — уравнение
кардиоиды.
— уравнение
кардиоиды.
в)
![]() ;
;
![]() ;
;
![]() ;
;
(х2+у2)2=2ху — уравнение лемнискаты Бернулли. ◄
№4. Данные уравнения линий в декартовых координатах записать в полярных координатах:
а)
у2=16+8х;
б)
![]() .
.
►а)
![]() — уравнение параболы;
— уравнение параболы;
б)
![]() ;
;
![]() ;
;
![]() — уравнение
кардиоиды. ◄
— уравнение
кардиоиды. ◄
Вариант 1
-
Построить точки:
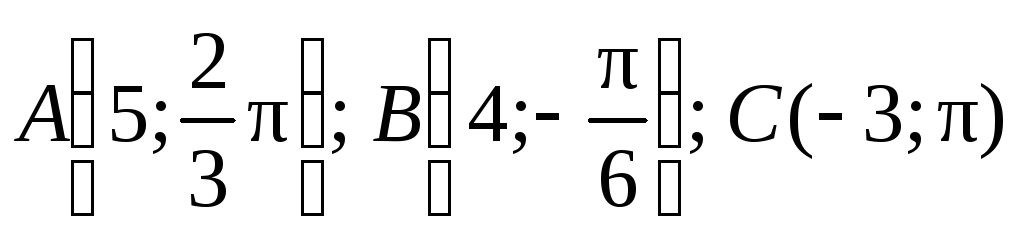 .
. -
Построить линии: 1)
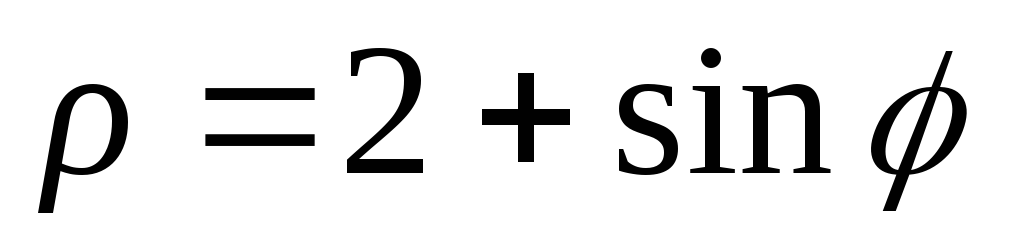 ;
2)
;
2)
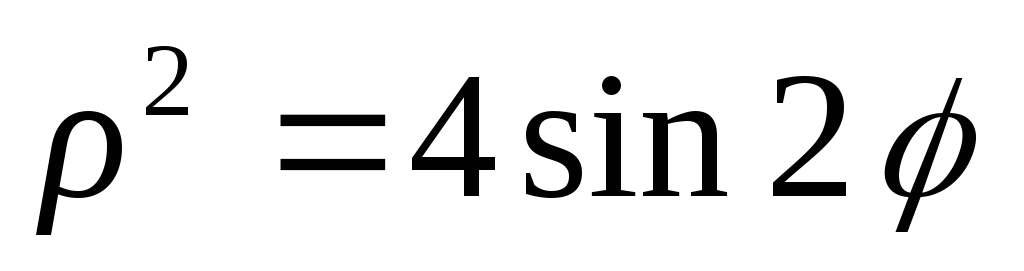 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
 ;
2)
;
2)
 .
.
Вариант 2
-
Построить точки:
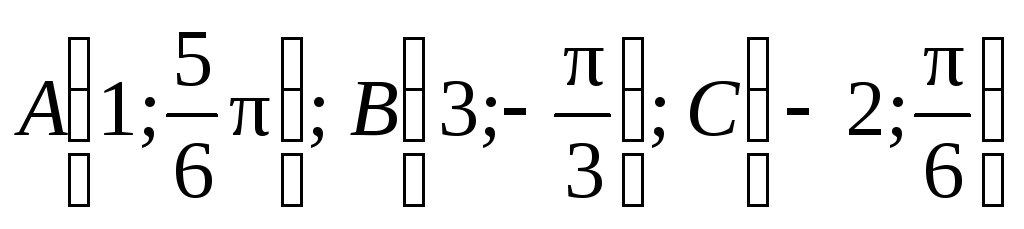 .
. -
Построить линии: 1)
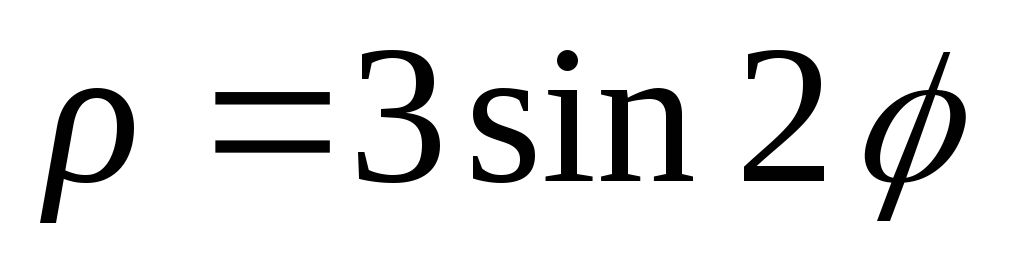 ;
2)
;
2)
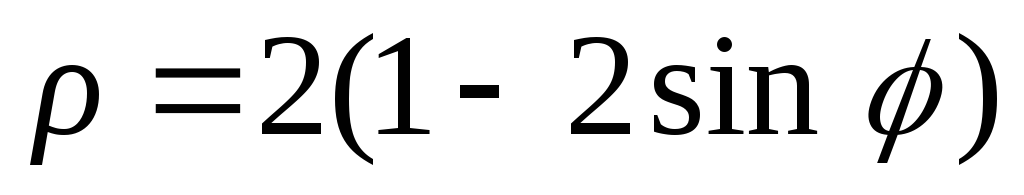 ;
3)
;
3)
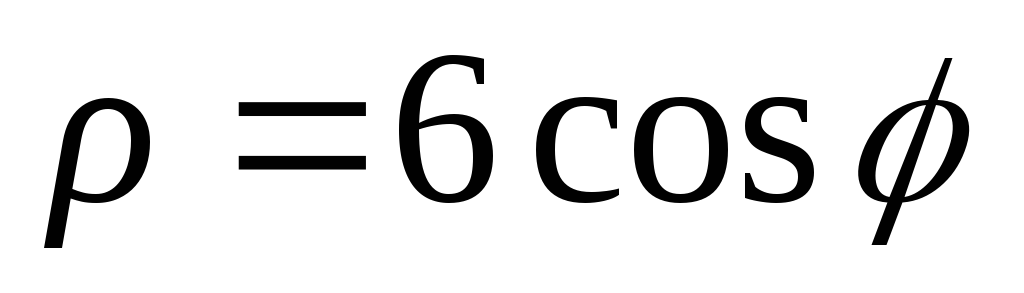 .
. -
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
 ;
2)
;
2)
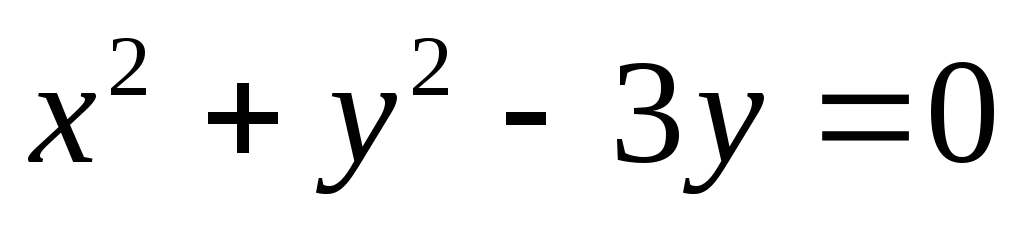 .
.
Вариант 3
-
Построить точки:
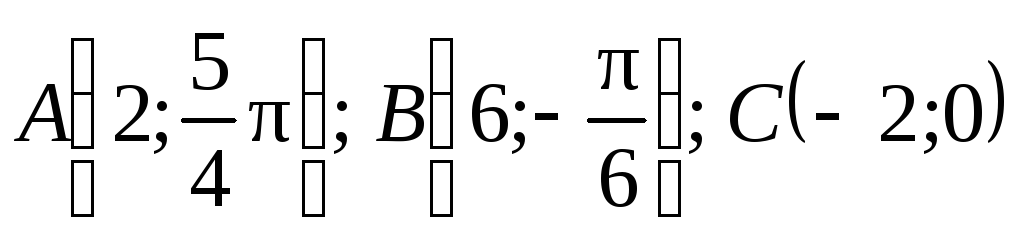 .
. -
Построить линии: 1)
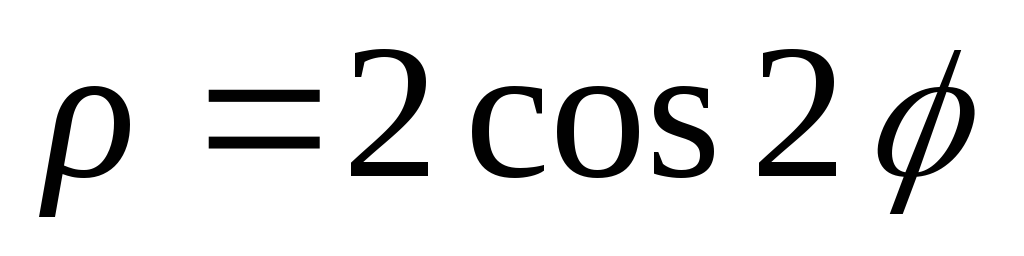 ;
2)
;
2)
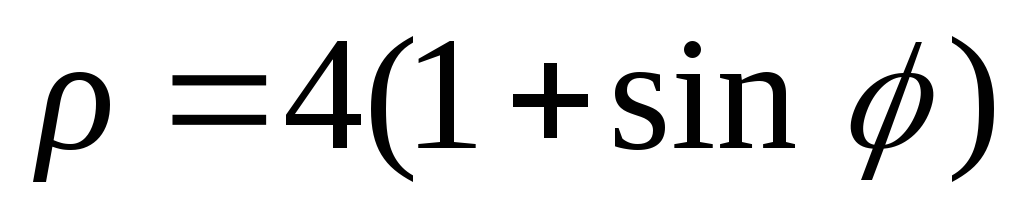 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
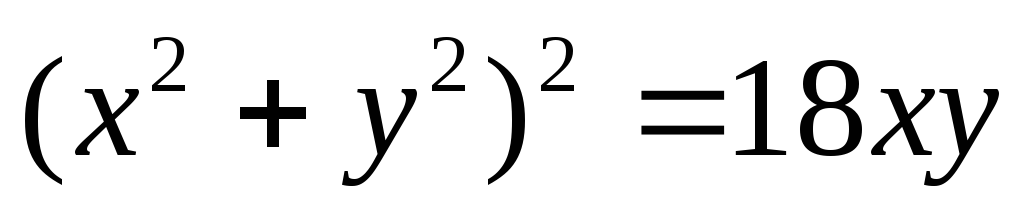 ;
2) у=8х.
;
2) у=8х.
Вариант 4
-
Построить точки:
 .
. -
Построить линии: 1)
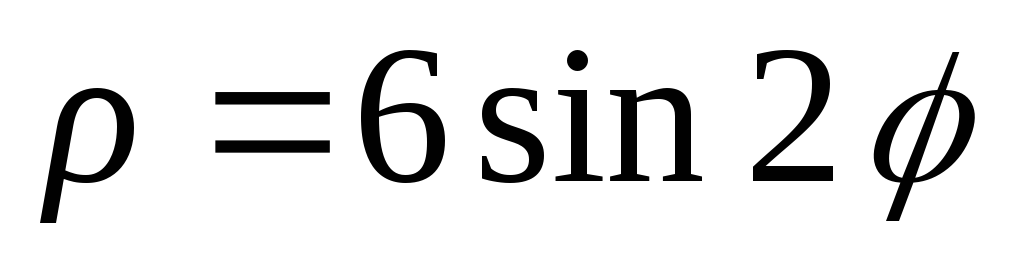 ;
2)
;
2)
 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
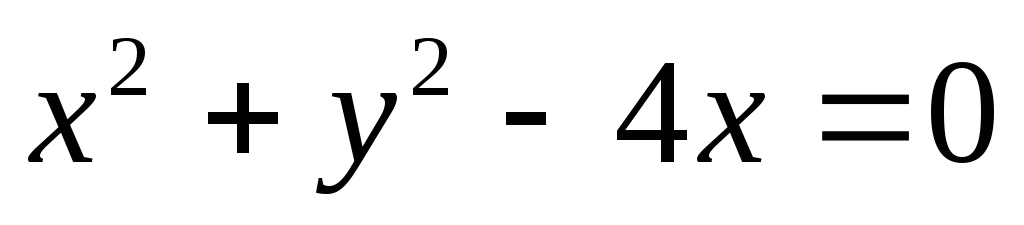 ;
2)
;
2)
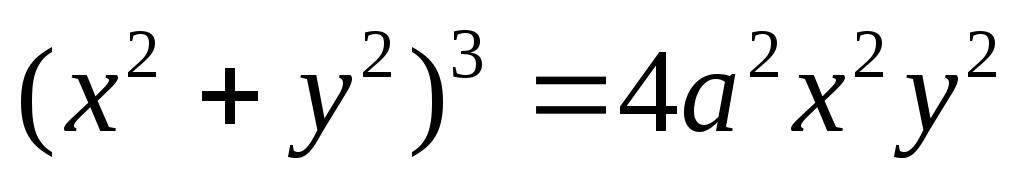 .
.
Вариант 5
-
Построить точки:
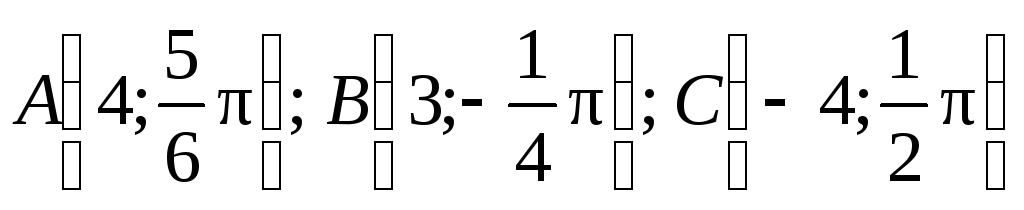 .
. -
Построить линии: 1)
 ;
2)
;
2)
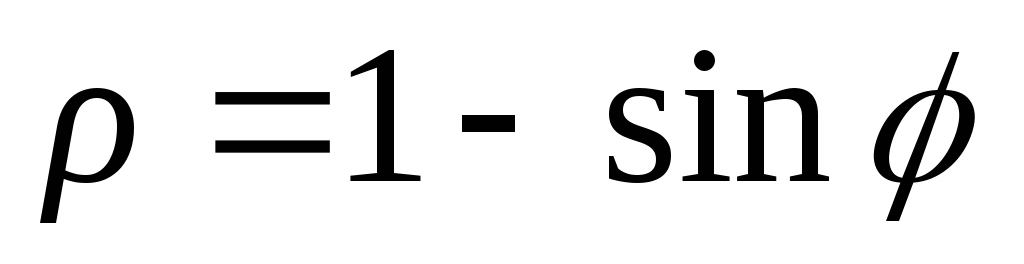 ;
3)
;
3)
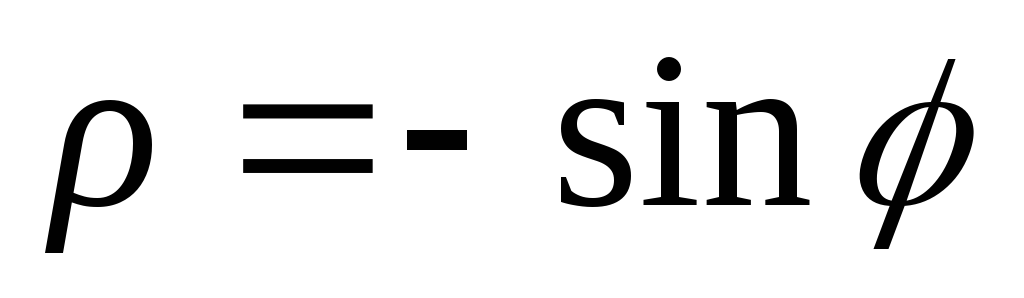 .
. -
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
 ;
2)
;
2)
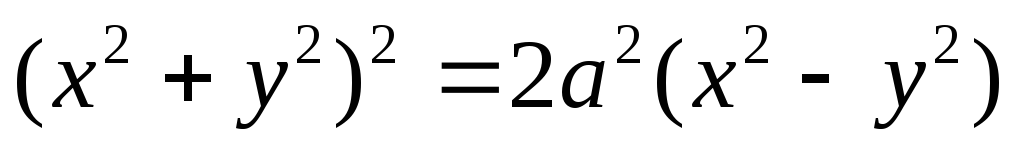 .
.
Вариант 6
-
Построить точки:
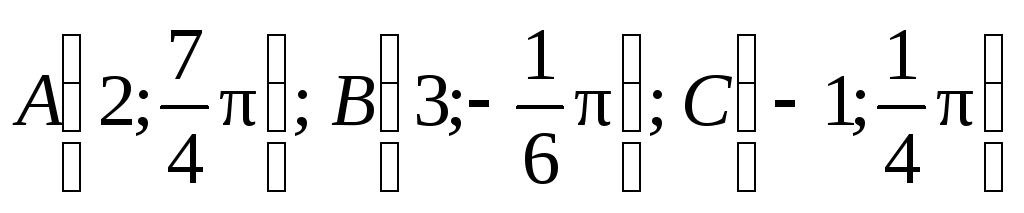 .
. -
Построить линии: 1)
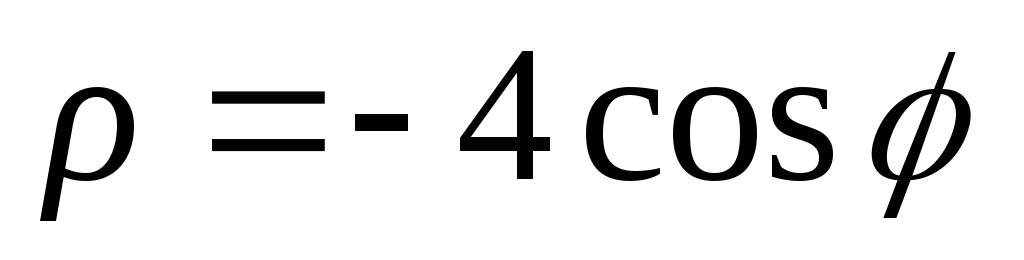 ;
2)
;
2)
 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах:
1)
![]() ;
2) х2 – 3у2 – 6х=0.
;
2) х2 – 3у2 – 6х=0.
Вариант 7
-
Построить точки:
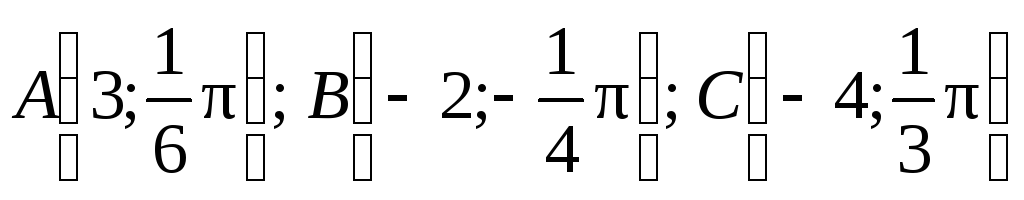 .
. -
Построить линии: 1)
 ;
2)
;
2)
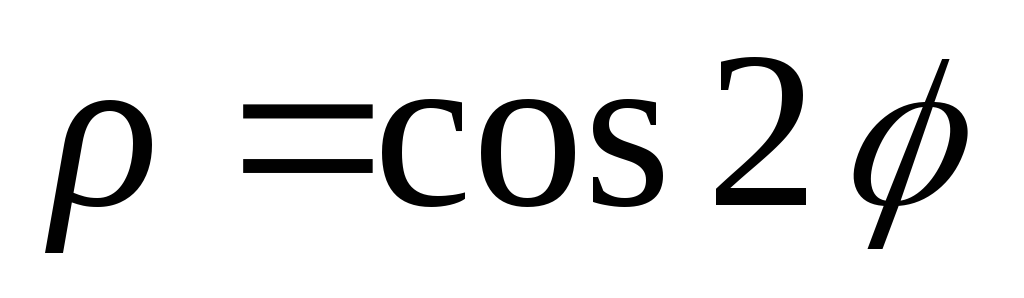 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах:
1)
![]() ;
2)
;
2)
![]() .
.
Вариант 8
-
Построить точки:
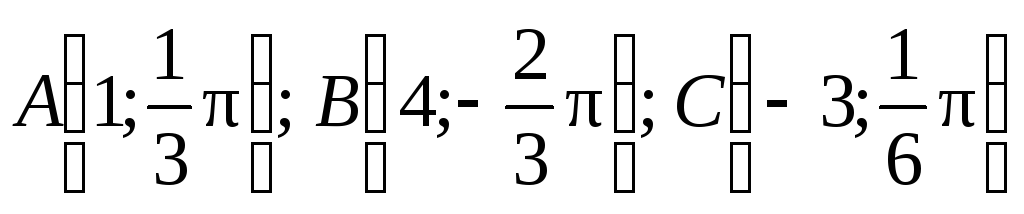 .
. -
Построить линии: 1)
 ;
2)
;
2)
 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
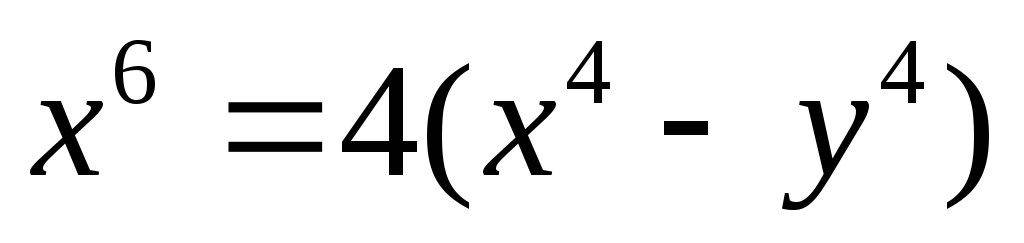 ;
;
2)
![]() .
.
Вариант 9
-
Построить точки:
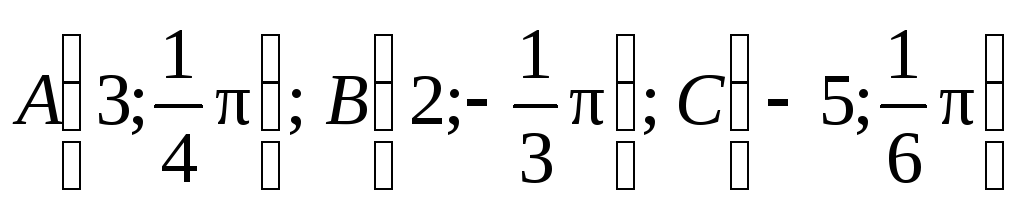 .
. -
Построить линии: 1)
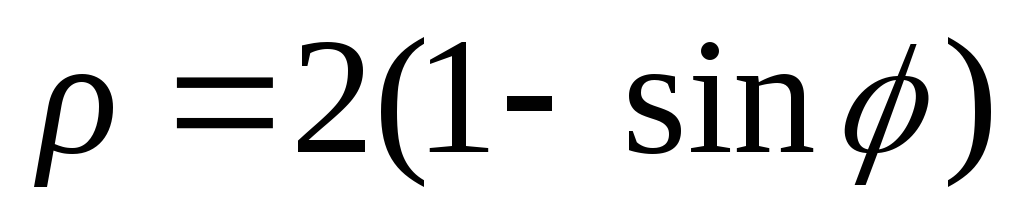 ;
2)
;
2)
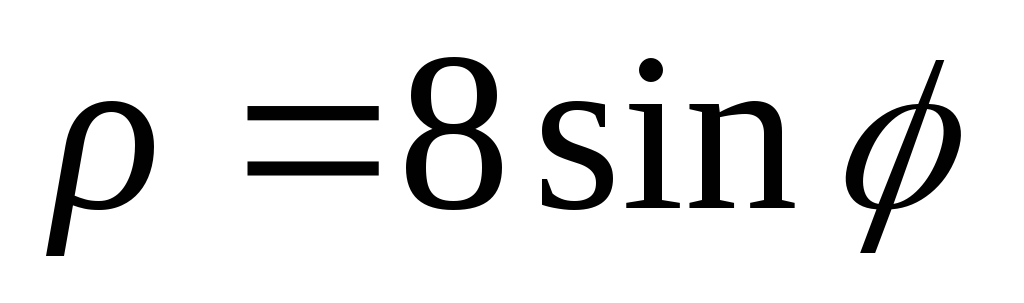 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах:
1)
![]() ;
2)
;
2)
![]() .
.
Вариант 10
-
Построить точки:
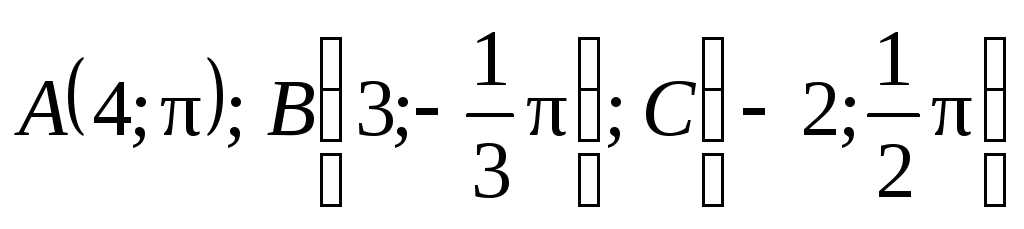 .
. -
Построить линии: 1)
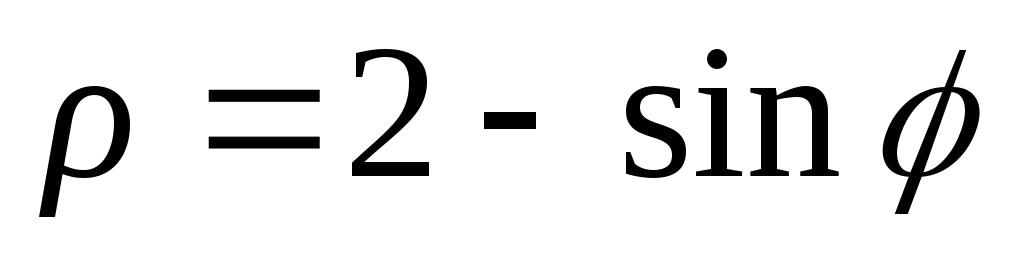 ;
2)
;
2)
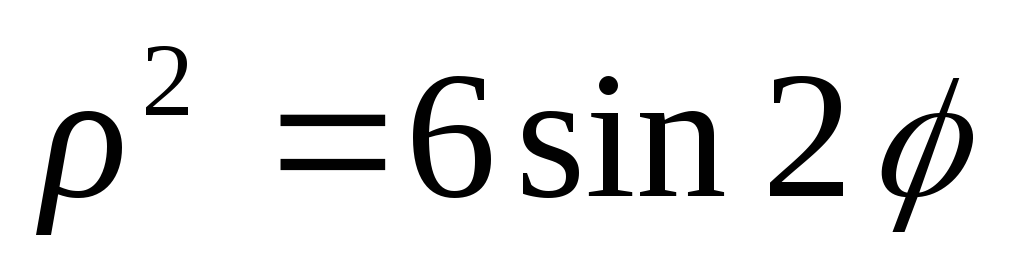 ;
;
3)
![]() .
.
-
Записать в декартовых координатах уравнения п.2.
-
Данные уравнения линий в декартовых координатах записать в полярных координатах: 1)
 ;
2)
;
2)
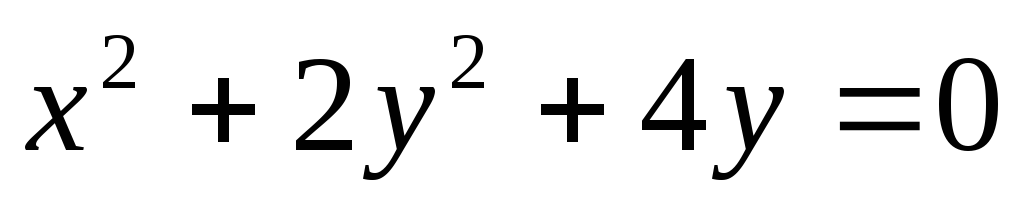 .
.
