
- •Занятие 1 Прямоугольная система координат
- •Занятие 2 Различные виды уравнения прямой на плоскости Цели
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Прямая на плоскости»
- •Занятие 3 Кривые второго порядка Цели
- •1. Эллипс
- •2. Окружность
- •3. Гипербола
- •4. Парабола
- •Различные виды парабол
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 4 Уравнение кривых второго порядка с осями симметрии, параллельными координатным осям. Параметрические уравнения линий
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 5 Полярная система координат
- •Аудиторное задание
- •Задание и общие указания
- •Инструкция к работе
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Кривые второго порядка»
- •Задание 5. Построить кривую, заданную параметрическими уравнениями:
- •Контрольные вопросы
- •Кривые второго порядка
- •Параметрические уравнения
- •Полярная система координат
- •Примерный вариант контрольной работы Вариант 1
- •Литература
- •Содержание
Занятие 4 Уравнение кривых второго порядка с осями симметрии, параллельными координатным осям. Параметрические уравнения линий
Цели
Знать:
-
Основные способы преобразования прямоугольных координат;
-
уравнение кривых второго порядка с осями симметрии, параллельными координатным осям.
Уметь:
-
переходить от одной прямоугольной системы координат к другой;
-
строить параллельно-смещённую кривую второго порядка по её уравнению.
Уравнения смещённых кривых второго порядка имеет вид:
![]() — эллипс;
— эллипс;
![]() — гипербола,
— гипербола,
где (х0; у0) — координаты центра кривой.
Уравнения смещённой параболы:
![]() ,
,
![]() ,
,
![]() ,
,
![]()
где (х0;у0) — координаты вершины параболы.
Теорема.
Уравнение
вида
![]()
всегда определяет:
-
окружность (при А=С),
-
эллипс (при
 ),
), -
гиперболу (при
 ),
), -
параболу (при
 ).
).
При этом возможны случаи вырождения:
-
для эллипса (окружности) — в точку или мнимый эллипс (окружность),
-
для гиперболы — в пару пересекающихся прямых,
-
для параболы — в пару параллельных прямых.
Пусть относительно системы декартовых прямоугольных координат на плоскости задана некоторая линия. Эту линию можно рассматривать как траекторию пути, пройденного точкой, движущейся по какому-нибудь закону. Если абсцисса точки М(х; у) изменяется по закону x=x(t), а ордината — по закону y=y(t), где t — параметр, то уравнение линии записывается в виде:
 (38)
(38)
Эти уравнения называются параметрическими уравнениями линии.
Составить уравнение линии на плоскости в выбранной системе координат — это, значит, составить такое уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на этой линии, и не удовлетворяют координаты точек, которые на этой линии не лежат.
Постановка задачи: Составить уравнение линии на плоскости.
План решения: 1. Выбрать на плоскости систему координат;
2. на линии, уравнение которой выводится, взять произвольную точку с координатами (х; у). Основываясь на заданном свойстве всех точек, лежащих на линии, составить уравнение, связывающее координаты произвольной точки с некоторыми постоянными величинами, данными в задаче. Найденное уравнение и будет искомым.
№13. Даны точка А(1; 0) и прямая х=2. В декартовых координатах составить уравнение линии, каждая точка М(х; у) которой:
1) в два раза ближе к точке А, чем к данной прямой;
2) в два раза дальше от точки А, чем от заданной прямой;
3) равноудалена от точки А и от прямой х=2.
► 1) Пусть М — точка искомой линии (рис 13).

рис.13
По условию 2МА=МN.Отсюда, так как N(2; y), то
![]() ;
;
![]() ;
;
4х2 – 8х+4+4у2=х2 – 4х+4;
3х2 – 4х+4у2=0;
![]() ;
;
![]() ;
;
![]() ;
;
домножим
на
![]() ,
имеем:
,
имеем:
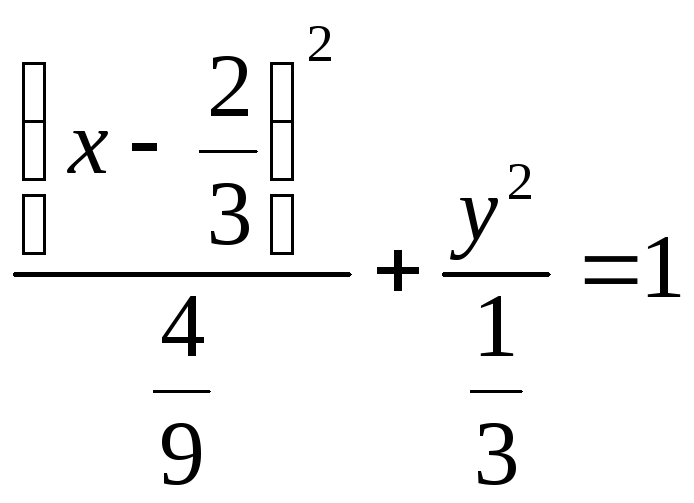 — уравнение
эллипса, который смещён относительно
системы координат XОY,
таким образом, что центр эллипса находится
в точке
— уравнение
эллипса, который смещён относительно
системы координат XОY,
таким образом, что центр эллипса находится
в точке
![]() ,
точка А
— совпадает с правым фокусом, х=2
— правая директриса.
,
точка А
— совпадает с правым фокусом, х=2
— правая директриса.
2) По условию МА=2МN. Отсюда, так как N(2; y), то
![]() ;
;
х2 – 2х+1+у2=4х2 – 16х+16;
3х2 – 14х – у2+15=0;
![]() ;
;
![]() ;
;
![]()
домножим
данное выражение на
![]() ,
имеем:
,
имеем:
 — уравнение
гиперболы, которая смещёна относительно
системы координат XОY,
таким образом, что центр гиперболы
находится в точке
— уравнение
гиперболы, которая смещёна относительно
системы координат XОY,
таким образом, что центр гиперболы
находится в точке
![]() ,
точка А
совпадает с её левым фокусом, х=2
— левая директриса.
,
точка А
совпадает с её левым фокусом, х=2
— левая директриса.
3) По условию МА=МN. Отсюда, так как N(2; y), то
![]() ;
;
х2 – 2х+1+у2=х2 – 4х+4;
у2= –2х+3;
![]() — уравнение
параболы, которая смещёна относительно
системы координат XОY,
таким образом, что вершина находится в
точке
— уравнение
параболы, которая смещёна относительно
системы координат XОY,
таким образом, что вершина находится в
точке
![]() ,
точка А
совпадает с фокусом, прямая х=2
— директриса. ◄
,
точка А
совпадает с фокусом, прямая х=2
— директриса. ◄
