2. Окружность

▼ Окружностью называется геометрическое место точек, равноудалённых от данной точки, называемой центром окружности (рис.7);

Каноническое уравнение окружности:

(19). ▲

рис.7

3. Гипербола

▼ Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а) (рис. 8 а, б).

Каноническое уравнение гиперболы:

, (20)

где а — длина действительной полуоси; b — длина мнимой полуоси. ▲

а) б)

рис. 8

А₁(а; 0) и А₂(–а; 0) — вершины гиперболы; отрезок А₁А₂=2а — вещественная осью гиперболы; b — мнимая полуось, F₁(–c; 0), F₂(c; 0) — координаты фокусов гиперболы, F₁F₂=2c — расстояние между фокусами гиперболы.

Зависимость между параметрами a, b и с выражается соотношением:

с²=a²+b².

Уравнение асимптот гиперболы: .

Эксцентриситет гиперболы: .

Уравнения директрис: .

Фокальные радиусы: .

Две гиперболы и называются сопряженными, если они имеют одни и те же полуоси и одни и те же асимптоты, но вещественная ось одной служит мнимой осью другой, и наоборот.

4. Парабола

▼ Параболой называется геометрическое место точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой (рис.9).

Каноническое уравнение параболы

у²=2рх, (22)

р — расстояние от фокуса F до директрисы (p>0). ▲

рис.9

вершина параболы — начало координат, ось симметрии — ось абсцисс, — фокус параболы.

Уравнение директрисы: .

Фокальный радиус: .

Эксцентриситет параболы =1.

Различные виды парабол

• Парабола симметрична относительно оси ОХ и направлена в её отрицательном направлении (рис.10)

у²= – 2 р х, (p>0) (23)

координаты фокуса ; уравнение директрисы .

• Парабола симметрична относительно оси ОY и направлена в её положительном направлении (рис.11)

х²=2 р у, (p>0) (24)

координаты фокуса , уравнение директрисы .

• Парабола симметрична относительно оси ОY и направлена в отрицательном направлении (рис.12)

х²= –2 р у, (p>0). (25)

координаты фокуса , уравнение директрисы .

рис. 10 рис.11 рис.12

№6. Написать уравнение окружности с центром в точке С(–2; 3) и радиусом R=5.

► По условию a= –2, b=3, R=5, следовательно, по формуле (15) получаем искомое уравнение окружности:

(х+2)²+(у–3)²=25, или х²+у²+4х–6у–12=0. ◄

№7. Найти полуоси, фокусы и эксцентриситет эллипса 4х²+9у²=16.

► Разделив на 16 обе части уравнения, получим каноническое уравнение эллипса:

или .

Сравнивая это уравнение с (16), находим: а² = 4; a=2; b²=; b=; =, следовательно, фокусы имеют координаты , , тогда эксцентриситет равен: . ◄

№8. На эллипсе 16х²+25у²=400 найти точку, расстояние от которой до правого фокуса в четыре раза меньше расстояния до левого фокуса.

► Разделив обе части уравнения на 400, находим каноническое уравнение эллипса:

,

откуда a²=25, a=5, b²=16, b=4, c²=25 – 16=9, c=3, .

В силу формулы (18) расстояния до фокусов выразятся так: . По условию r₁=4r₂, следовательно, , откуда х=5.

Подставляя это значение в уравнение эллипса, получим у=0, следовательно, искомая точка М(5; 0).◄

№9. Составить уравнение гиперболы, если расстояние между вершинами её равно 20, а расстояние между фокусами 30.

► Вершины гиперболы лежат на её действительной оси. По условию 2а=20; 2с=30. значит, а=10; с=15; а²=100; с²=225. Для гиперболы с²=а²+b², отсюда b²=с² – а²=225 – 100=125. Тогда уравнение гиперболы имеет вид: . ◄

№10. Гипербола проходит через точки и . Найти уравнение гиперболы.

► Уравнение гиперболы может быть записано:

b²x² – a²y²=a²b².

Для решения задачи следует определить а² и b². Подставим в это уравнение координаты заданных точек, получим:

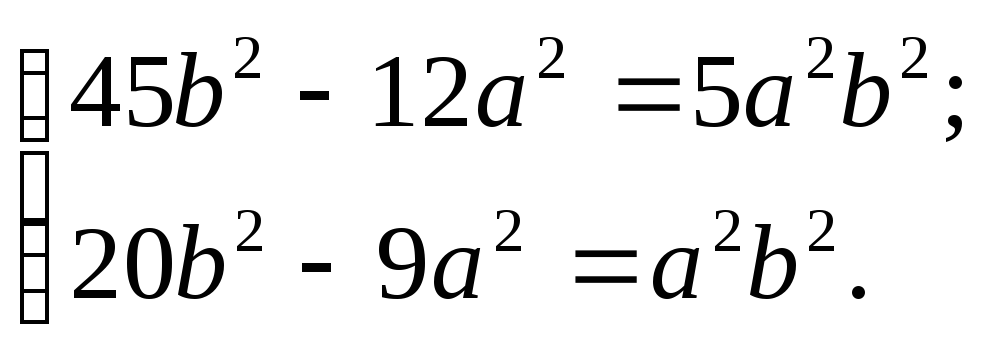
Разрешив полученную систему имеем:

а²=5, b²=3.

Подставляя найденные значения а² и b² получим, что искомое уравнение имеет вид 3х² – 5у²=15. ◄

№11. Найти координаты фокуса и уравнение директрисы параболы у²=8х. Вычислить расстояние от точки М(2; 4) до фокуса.

► Сравнивая данное уравнение с (26), находим, что

2р=8, откуда р=4, =2.

В соответствии с формулой (27) получаем уравнение директрисы параболы х= – 2; фокус параболы находится в точке F(2; 0).

Точка М(2; 4) лежит на параболе, так как её координаты удовлетворяют уравнению у²=8х. По формуле (29) находим фокальный радиус точки М: r=2+2=4. ◄

№12. Составить уравнение параболы, симметричной относительно оси ОХ и проходящей через точки А(5; 4) и В(15; –6).

► Так как парабола симметрична относительно оси ОХ, то ее уравнение имеет вид:

у²=2рх+с,

где р и с — некоторые постоянные. Найдём эти постоянные. Поскольку точки А и В лежат на параболе, то их координаты должны удовлетворять её уравнению, составим систему уравнений:

Из полученной системы находим р=1, с=6.

Таким образом, данная парабола определяется уравнением у²=2х+6. ◄