
- •Занятие 1 Прямоугольная система координат
- •Занятие 2 Различные виды уравнения прямой на плоскости Цели
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Прямая на плоскости»
- •Занятие 3 Кривые второго порядка Цели
- •1. Эллипс
- •2. Окружность
- •3. Гипербола
- •4. Парабола
- •Различные виды парабол
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 4 Уравнение кривых второго порядка с осями симметрии, параллельными координатным осям. Параметрические уравнения линий
- •Аудиторные задания
- •Домашние задания
- •Дополнительные задания
- •Занятие 5 Полярная система координат
- •Аудиторное задание
- •Задание и общие указания
- •Инструкция к работе
- •Домашние задания
- •Дополнительные задания
- •Решение типового варианта индивидуального домашнего задания «Кривые второго порядка»
- •Задание 5. Построить кривую, заданную параметрическими уравнениями:
- •Контрольные вопросы
- •Кривые второго порядка
- •Параметрические уравнения
- •Полярная система координат
- •Примерный вариант контрольной работы Вариант 1
- •Литература
- •Содержание
Кривые второго порядка
-
Какие из следующих уравнений являются уравнениями эллипсов: а)
 ;
б)
;
б)
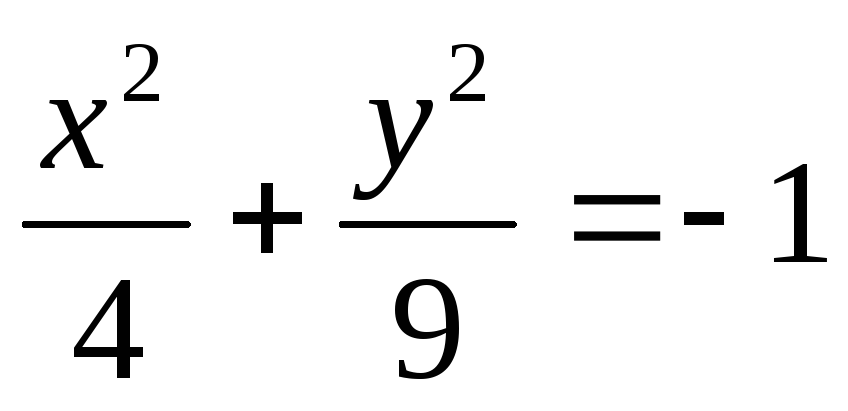 ;
;
в)
![]() ;
г)
;
г)
![]() ;
д.)
;
д.)
![]() ;
;
е.)
![]() ?
?
-
При каких значениях p точка (p; 3) принадлежит эллипсу
 ?
? -
Верно ли, что произведение полуосей эллипса
 равно 36?
равно 36? -
Чему равны полуоси эллипса
 ?
? -
Верно ли, что расстояние между противоположными вершинами эллипса
 равны 6 и 2?
равны 6 и 2? -
При каких значениях m уравнение
 является уравнением эллипса?
является уравнением эллипса? -
При каких значениях p прямая х=р имеет с эллипсом
 ровно одну общую точку?
ровно одну общую точку? -
Чему равен радиус окружности, сжатием которой к оси ОX получен эллипс
 ?
? -
Найти уравнение гиперболы, симметричной относительно осей координат и касающейся прямой
х – у – 2=0 в точке М(4; 2).
-
Доказать, что отношение расстояний от любой точки гиперболы до фокуса и до соответствующей директрисы есть величина постоянная, равная
 .
. -
Какие линии определяются следующими уравнениями: 1)
 ;
2)
;
2)
 ?
? -
Доказать оптическое свойство параболы: луч света, исходящий из фокуса параболы, отразившись от неё, идёт по прямой, параллельной оси этой параболы.
-
Из фокуса параболы у2=12х под острым углом
 к оси ОX
направлен луч света. Известно, что
к оси ОX
направлен луч света. Известно, что
 .
Дойдя до параболы, луч от неё отразился.
Составить уравнение прямой, на которой
лежит отражённый луч.
.
Дойдя до параболы, луч от неё отразился.
Составить уравнение прямой, на которой
лежит отражённый луч. -
Каково уравнение параболы с вершиной в точке О(0; 0), если уравнение её директрисы 2у+7=0?
-
Каково будет уравнение параболы у2=4х, если её ось симметрии повернуть на
 на
на
 на –
на –
Параметрические уравнения
-
Является ли окружностью линия:
а)
![]()
б)
![]()
в)![]()
г)
![]() ?
?
-
Является ли линия
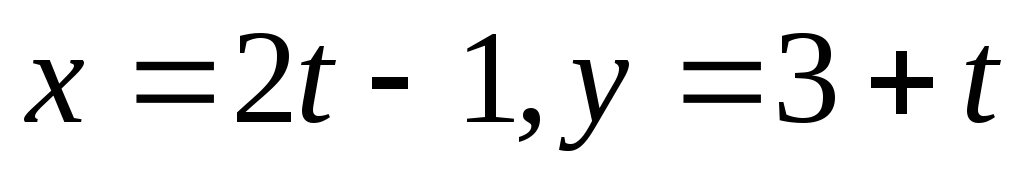 прямой?
прямой? -
Могут ли различные параметрические уравнения определять одну и ту же кривую?
-
Проходит ли траектория
 через точку (2; –1)?
через точку (2; –1)? -
При каких значениях параметра t точки траектории
 лежат в нижней полуплоскости?
лежат в нижней полуплоскости? -
При каких значениях параметра t точки траектории
 имеют отрицательные абсциссы?
имеют отрицательные абсциссы? -
В какой точке началось движение по закону:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Может ли точка двигаться равномерно и прямолинейно по закону
 ?
? -
По какой траектории движется точка, если закон её движения имеет вид:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ?
?
Полярная система координат
-
Как расположены точки, полярные координаты которых удовлетворяют уравнению: 1)
 ;
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ?
?
-
Каковы координаты точки В полярной оси, отстоящей от точки
 на 7 единиц?
на 7 единиц?
Примерный вариант контрольной работы Вариант 1
-
На биссектрисе первого координатного угла лежат точки А(3; 3) и В(х; у), расстояние между которыми
 .
Найти координаты точки В.
.
Найти координаты точки В. -
Найти уравнение прямой, проходящей через точку пересечения прямых 2х – у – 1=0 и 3х – у+4=0 параллельно прямой 4х+2у – 13=0.
-
Найти угол между высотой AD и медианой АЕ в треугольнике с вершинами в точках А(1; 3), В(4; –1), С( –1; 1).
-
Найти каноническое уравнение эллипса, если:
а) расстояние между концами большой и малой оси равно 5, а сумма длин полуосей равна 7;
б) расстояние от его фокуса до концов большой оси равны 2 и 14.
-
Через фокус параболы у2= –х проведена прямая под углом
 к оси ОX.
Найти длину образовавшейся хорды.
к оси ОX.
Найти длину образовавшейся хорды. -
Какую линию определяет уравнение
4х2+9у2 – 8х – 36у+4=0?
Вариант 2
-
Дан треугольник АВС с вершинами А(1; 5), В(4; 1), С(13; 10). Найти точку пересечения биссектрисы внутреннего угла А со стороной ВС.
-
Прямая y=kx+4 удалена от начала координат на расстояние
 .
Найти значение k.
.
Найти значение k. -
Даны последовательные вершины параллелограмма ABCD: А( –2; 5), В(2; 7), С( –4; –3). Найти координаты четвёртой вершины D и написать уравнение диагонали BD.
-
Найти уравнение прямой, содержащей диаметр окружности х2+у2 – 6х+4у+8=0, перпендикулярный прямой х – 3у+2=0.
-
Найти уравнение гиперболы, зная, что её эксцентриситет ε=2, фокусы гиперболы совпадают с фокусами эллипса
 .
. -
Какую линию определяет уравнение
х2 – 9у2+2х+36у – 44=0?
