
- •13.1 Определение линейного пространства
- •13.2 Линейная зависимость, размерность и базис в линейном пространстве
- •Примеры базисов в линейных пространствах
- •13.3 Подмножества линейного пространства
- •13.4. Операции с элементами линейного пространства в координатном представлении
- •13.5. Изоморфизм линейных пространств
Примеры базисов в линейных пространствах
|
Линейное пространство
|
Размерность |
Пример базиса |
|
Множество всех радиусов-векторов на плоскости |
2 |
Упорядоченная пара неколлинеарных векторов на плоскости. |
|
Множество всех векторов в пространстве
|
3 |
Упорядоченная тройка нормированных, попарно ортогональных векторов. |
|
Множество всех n-компонентных столбцов |
n |
n
cтолбцов вида
|
|
Множество
всех матриц размера
|
nm |
nm
всевозможных различных матриц размера
|
|
Множество решений однородной системы m уравнений с n неизвестными и рангом основной матрицы r |
|
Нормальная фундаментальная система решений. |
13.3 Подмножества линейного пространства
Подпространство
Определение. Непустое
множество
 ,
образованное из элементов линейного
пространства R,
называется подпространством
этого линейного пространства, если для
любых
,
образованное из элементов линейного
пространства R,
называется подпространством
этого линейного пространства, если для
любых
 и любого числа
и любого числа
 :
:
(1)
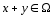 , (2)
, (2)
 .
.
Замечание. Из
этого определения следует, что множество
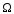 само является линейным пространством,
поскольку для него, очевидно, выполняются
все аксиомы операций в линейном
пространстве.
само является линейным пространством,
поскольку для него, очевидно, выполняются
все аксиомы операций в линейном
пространстве.
Примеры. 1. Множество радиусов-векторов всех точек, лежащих на некоторой плоскости, проходящей через начало координат, является подпространством во множестве радиусов-векторов всех точек трехмерного геометрического пространства.
2.
В пространстве n-мерных
столбцов совокупность решений однородной
системы линейных уравнений с n
неизвестными
и с основной матрицей ранга r
образует подпространство размерности
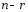 .
.
3. Подпространством любого линейного пространства будет:
а) само линейное пространство;
б) множество, состоящее из одного нулевого элемента.
Определение. Пусть
даны два подпространства
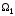 и
и
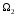 линейного пространства R.
Тогда
линейного пространства R.
Тогда
1.
Объединением
подпространств
 и
и
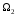 называется множество элементов
называется множество элементов
 ,
таких, что
,
таких, что
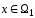 либо
либо
 .
Объединение подпространств
.
Объединение подпространств
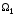 и
и
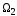 обозначается
обозначается
 .
.
2.
Пересечением
подпространств
 и
и
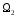 называется множество элементов
называется множество элементов
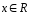 ,
принадлежащих
,
принадлежащих
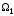 и
и
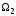 одновременно. Пересечение подпространств
одновременно. Пересечение подпространств
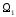 и
и
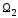 обозначается
обозначается
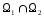 .
.
3.
Суммой
подпространств
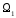 и
и
 называется совокупность всех элементов
называется совокупность всех элементов
 при условии, что
при условии, что
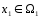 и
и
 .
Сумма подпространств
.
Сумма подпространств
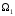 и
и
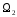 обозначается
обозначается
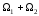 .
.
4.
Прямой
суммой
подпространств
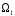 и
и
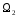 называется совокупность всех элементов
называется совокупность всех элементов
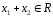 при условии, что
при условии, что
 и
и
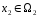 и
и
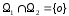 .
Прямая сумма обозначается
.
Прямая сумма обозначается
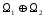 .
.
Сумма
и пересечение подпространств
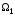 и
и
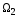 в R
также являются подпространствами в R.
в R
также являются подпространствами в R.
Теорема
13.5 Размерность
суммы
подпространств
 и
и
 равна
равна

Следствие. В случае прямой суммы подпространств
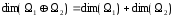
и
каждый элемент

 представим в виде
представим в виде
 так, что
так, что
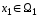 и
и
 ,
единственным
образом.
,
единственным
образом.
Линейная оболочка системы элементов
Определение. Совокупность
всевозможных линейных комбинаций
некоторого множества элементов
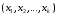 линейного пространства
линейного пространства
 называется линейной
оболочкой
этого множества и обозначается
называется линейной
оболочкой
этого множества и обозначается
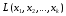 .
.
Пусть
задан набор элементов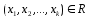 ,
порождающих линейную оболочку
,
порождающих линейную оболочку
 ,
тогда любой элемент этой линейной
оболочки имеет вид
,
тогда любой элемент этой линейной
оболочки имеет вид
 и справедлива теорема:
и справедлива теорема:
Теорема
13.6 Множество
всех элементов, принадлежащих линейной
оболочке
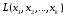 ,
является в R
подпространством размерности m
,
где m
– максимальное число линейно независимых
элементов в множестве
,
является в R
подпространством размерности m
,
где m
– максимальное число линейно независимых
элементов в множестве
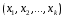 .
.
Гиперплоскость
Определение. Множество
 ,
образованное из элементов вида
,
образованное из элементов вида
 ,
где
,
где
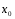 есть произвольный фиксированный элемент
линейного пространства R,
а x
– любой элемент некоторого подпространства
есть произвольный фиксированный элемент
линейного пространства R,
а x
– любой элемент некоторого подпространства
 ,
называется гиперплоскостью
(или линейным
многообразием)
в линейном пространстве
R.
,
называется гиперплоскостью
(или линейным
многообразием)
в линейном пространстве
R.
Замечание. В общем случае гиперплоскость не является подпространством.
Замечание. Если
 ,
то говорят о k-мерной
гиперплоскости.
,
то говорят о k-мерной
гиперплоскости.

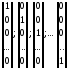 .
.
 ,
все элементы которых равны нулю, кроме
одного, равного 1.
,
все элементы которых равны нулю, кроме
одного, равного 1.