7.4. Сравнение бесконечно малых функций

Известно, что сумма, разность и произведение б. м. ф. есть б. м. ф.

Отношение б. м. ф. может быть конечным числом, или может быть б.м. ф., или может быть б. б. ф., или может вообще не стремиться ни к какому пределу.

Две б. м. ф. сравниваются между собой с помощью их отношения.

Пусть и являются б.м.ф. при .

1. Если , то называется б.м.ф. более высокого порядка, чем .

2. Если , то называется б.м.ф. более низкого порядка, чем .

3. Если , то и называются б. м. ф. одного порядка.

4. Если не существует, то и называются несравнимыми б.м.ф.

5. Если , то и называются эквивалентными б. м. ф.

Обозначаются эквивалентные б. м. ф. так:

Среди б. м. ф. эквивалентные б. м. ф. играют особую роль.

Свойства эквивалентных б. м. ф.

1. Предел отношения двух б. м. ф. не изменится, если каждую или одну из них заменить эквивалентной б. м. ф.

2. Разность двух эквивалентных б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.

3. Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.

Свойства эквивалентных б.м.ф. применяют для раскрытия неопределенностей при вычислении пределов.

Пример 1.

		(отбросили в числителе б. м. ф. более высокого порядка)
.	( заменили эквивалентной ей функцией при ).

Таблица эквивалентных б. м. ф.

1.	при
2.	при
3.	при
4.	при
5.	при
6.	при
7.	при
8.	при
9.	при
10. ,	при

§ 8. Вычисление пределов функции

Рассмотренные ранее способы вычисления пределов не охватывают все возможные случаи. При вычислении пределов могут появиться неопределенности вида , , .

На конкретных примерах рассмотрим способы раскрытия этих неопределенностей.

Пример 1.

(делим числитель и знаменатель дроби на в старшей степени)

.

При этом если в числителе и знаменателе многочлены одной степени, предел равен отношению коэффициентов при старших степенях. Если степень числителя больше степени знаменателя, то предел равен . Если степень числителя меньше степени знаменателя, то предел равен .

Пример 2.

( делим числитель и знаменатель на критический множитель )

		–
		–

.

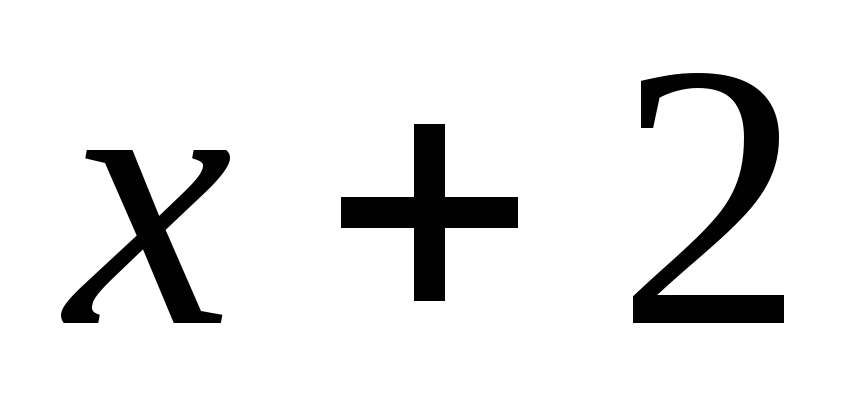
Пример 3.

(домножаем на сопряженные выражения числитель и знаменатель дроби)

.

Пример 4.

(выражение под знаком предела умножаем и делим на неполный квадрат суммы )

.
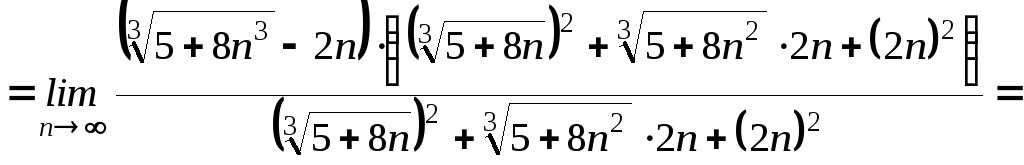