Контрольные варианты к задаче 12

Вычислить пределы функций:

.	.
.	.
.	.
.	.
. .	.
	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	28. .
.	.

З а д а ч а 13

Если в числителе или знаменателе стоят иррациональные выражения, то для получения сомножителя умножим числитель и знаменатель на сопряженные им выражения.

Пример 13

Вычислить .

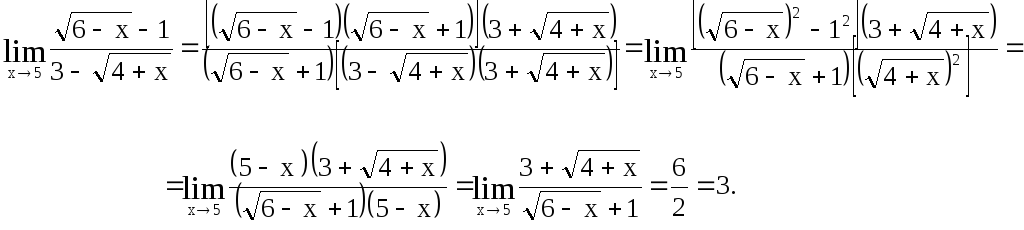
Контрольные варианты к задаче 13

Вычислить пределы функций:

1.	.	2.	.	3.	.
4.	.	5.	.	6.	.
7.	.	8.	.	9.	.
10.	.	11.	.	12.	.
13.	.	14.	.	15.	.
16.	.	17.	.	18.	.
19.	.	20.	.	21.	.
22.	.	23.	.	24.	.
25.	.	26.	.	27.	.
28.	.	29.	.	30.	.

З а д а ч а 14

Пример 14

Вычислить

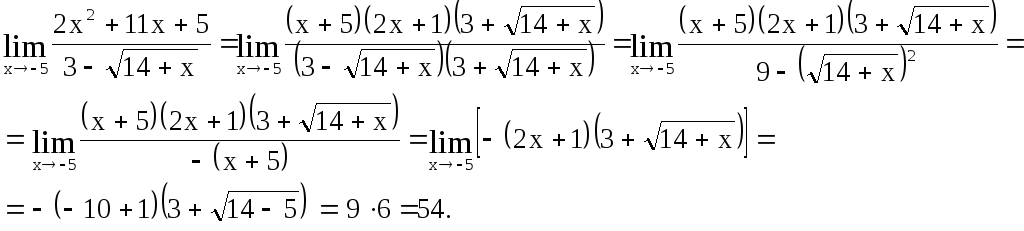
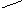
Контрольные варианты к задаче 14

Вычислить пределы функций:

.	.
.	.
.	.
.	8.
.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.

З а д а ч а 15

Если при и, то отношение представляет собой неопределенность . В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х.

Пример 15

Вычислить предел .

.

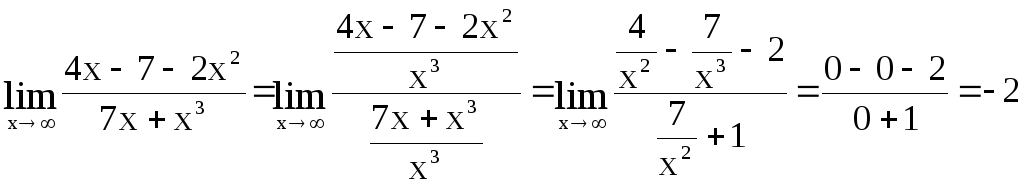Контрольные варианты к задаче 15

Вычислить пределы функций:

.	.
.	.
.	.
.	.
.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
.	.
	.
	.

З а д а ч а 16

Пример 16

Вычислить предел .

Здесь старшая степень при n – вторая и - степень, поэтому