Контрольные варианты к задаче 10
Найти
точку
,
симметричную точке М относительно
прямой (для вариантов 1-15) или плоскости
(для вариантов 16-30):
|
1.
|
|
2.
|
|
3.
|
|
4.
|
|
5.
|
|
6.
|
|
7.
|
|
8.
|
|
9.
|
|
10.
|
|
11.
|
|
12.
|
|
13.
|
|
14.
|
|
15.
|
|
16.
|
|
17.
|
|
18.
|
|
19.
|
|
20.
|
|
21.
|
|
22.
|
|
23.
|
|
24.
|
|
25.
|
|
26.
|
|
27.
|
|
28.
|
|
29.
|
|
30.
|
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.
З а д а ч а 11
Правило
1. Чтобы
вычислить
,
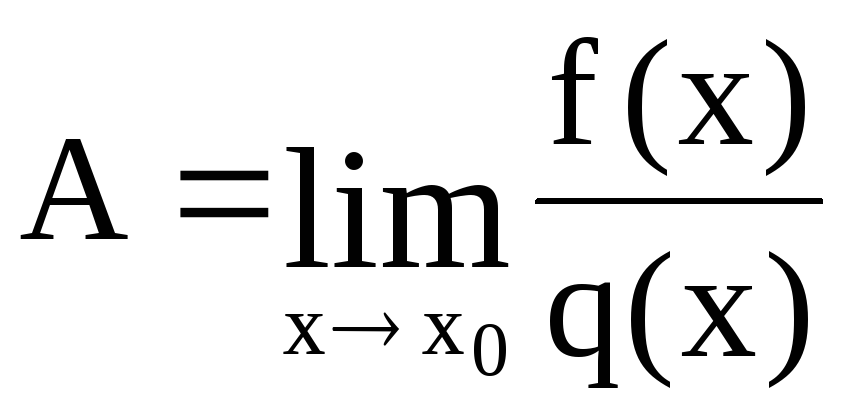нужно вместо переменной х поставить
её предельное значение
.
Если
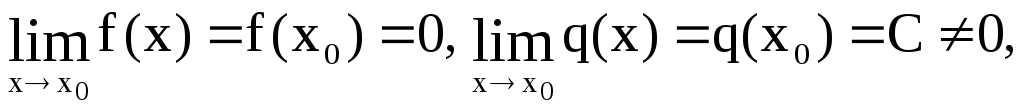то
Если
то
.
Если
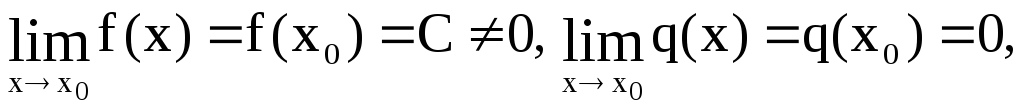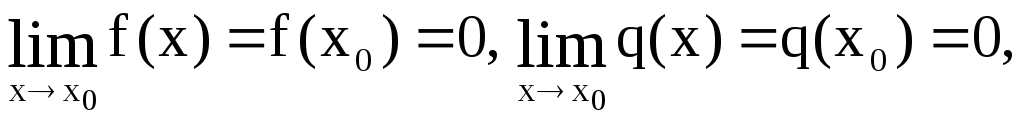то
- неопределенность.
Правило
2. Чтобы
раскрыть неопределенность
в алгебраическом выражении, надо в
числителе и знаменателе выделить
множитель
,
который стремится к нулю, и на него под
знаком предела сократить.
Правило
3. Если в
числителе и знаменателе стоят многочлены,
то чтобы получить множитель
,
нужно многочлены разложить на множители.
Пример 11
Вычислить
предел
.
.
Найдем
корни многочленов
.
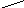
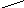
Контрольные варианты к задаче 11
Вычислить пределы функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
З а д а ч а 12
Пример 12
Вычислить
предел
.
В
числителе и знаменателе получаются
нули за счет сомножителя
,
который стремится к нулю при
.
Разложим многочлены на множители,
разделив их на
.
-
-
.
-
-
-
-
.
Замечание. При разложении многочлена в числителе можно было применить способ группировки и вынесения общего множителя, а в знаменателе найти корни, решив биквадратное уравнение.