Контрольные варианты задачи 25
Исследовать
функцию
на непрерывность. В точках разрыва
установить характер разрыва. Схематично
построить график функции:
|
1.
|
2.
|
3.
|
4.
|
5.
|
|
6.
|
7.
|
8.
|
9.
|
10.
|
|
11.
|
12.
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
19.
|
20.
|
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
26.
|
27.
|
28.
|
29.
|
30.
|
З а д а ч а 26
По
определению модуль числа
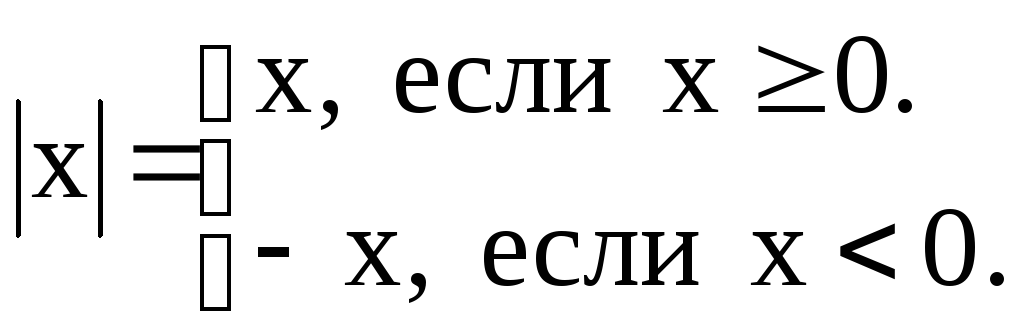
Следовательно,
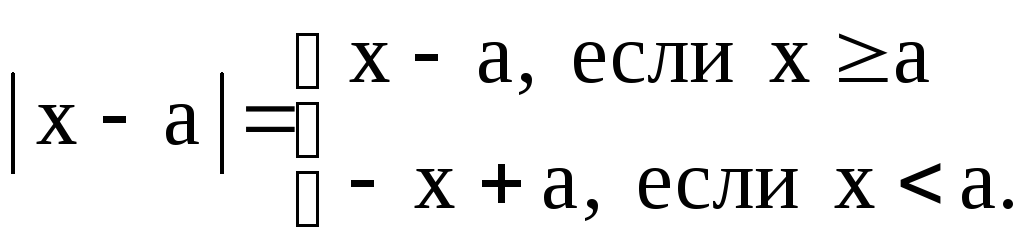
Пример 28
Исследовать функцию на непрерывность. Установить характер разрыва. Построить график функции
.
так
как
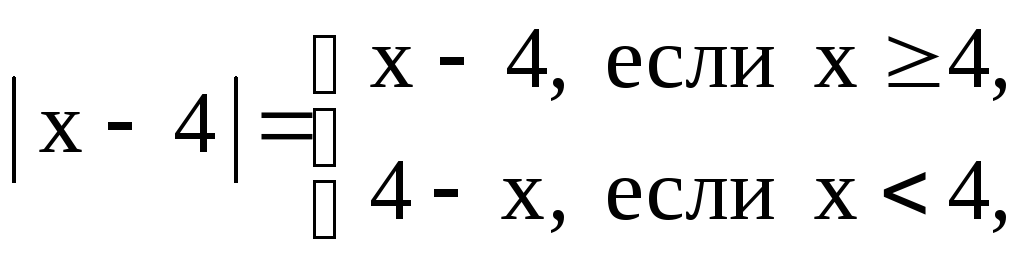
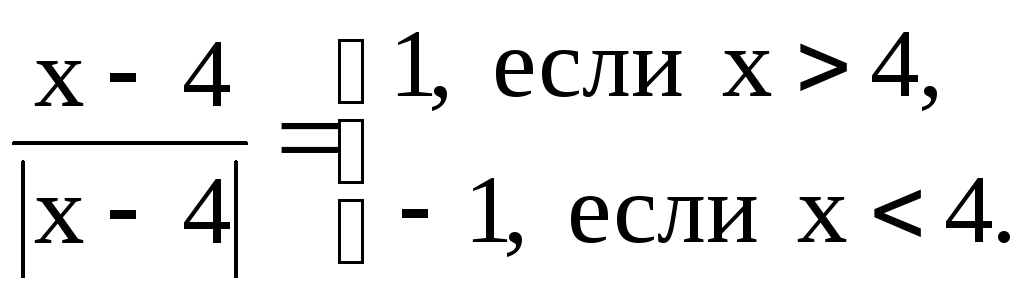
Функция
не определена в точке
.
Эта функция может быть записана в виде
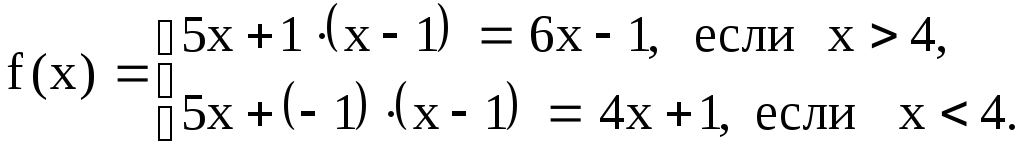
Каждое
из аналитических выражений непрерывно,
следовательно, функция
имеет разрыв только в точке
,
где она не определена. Слева от этой
точки
функция
задана формулой
.
Следовательно,
=
.
Справа от точки
функция задана формулой
,
поэтому
.
Односторонние пределы в точке
конечны, но не равны между собой. Предел
функции в точке
не существует. Функция имеет разрыв в
этой точке, который является неустранимым
разрывом I
рода (скачком).
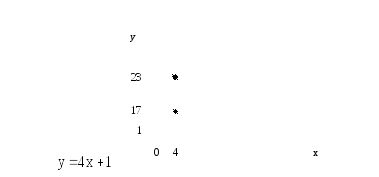
Контрольные варианты задачи 26
Исследовать функцию на непрерывность. В точках разрыва установить характер разрыва. Схематично построить график функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Библиографический список
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. М.: Наука, 1985. Т. 2.
2. Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 1980.
3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.: Наука, 1982.
4. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука, 1980.
5. Линейная алгебра и аналитическая геометрия (типовой расчет) / Сост.: Э.Г.Кучеренко, Н.И. Васильева, Р.Ш. Минабудинова; ОмПИ. Омск, 1983.
6. Данко П.Г. Высшая математика в упражнениях и задачах. М.: Высш. школа, 1980.
7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.
Редактор Г. М. Кляут
ИД 06039 от 12.10.01
Сводный темплан 2004 г.
Подписано в печать 12.07.04. Бумага офсетная. Формат 60 х 84 1/16
Отпечатано на дупликаторе. Усл. печ. л. 3,5. Уч.-изд. л. 3,5.
Тираж 100 экз. Заказ
Издательство ОмГТУ.644050, г. Омск, пр-т Мира, 11.
Типография ОмГТУ