Лабораторные работы / №1лаба по ЛСУ

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

Кафедра: «Управление и информатика в технических системах»

ЛАБОРАТОРНАЯ РАБОТА № 1

по дисциплине «Локальные системы управления»

Выполнил ст. гр. УИТ-53В

Тараскина Е.Е.

Приняла:

Скоробогатова Т.Н

Балаково 2009

Цель работы: Изучить методы исследования устойчивости стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР.

Дано:

где, k = 1.2; Т₁ = 0,8; Т₂ = 2,5

Порядок выполнения работы

1) Подсчитаем передаточную функцию для замкнутой и разомкнутой системы:

2) Определим устойчивость системы по критерию Гурвица:

Для устойчивости системы необходимо и достаточно, чтобы все миноры определителя Гурвица были положительны.

Характеристическое уравнение имеет вид:

a0 = 160; а1 = 104; а2 = 18,5; а3 = 1

Запишем определитель Гурвица:

Система устойчива.

3) Определим устойчивость по критерию Льенора Шипора.

Для устойчивости системы необходимо и достаточно, чтобы диагональные миноры определителя Гурвица с нечетными (четными) индексами были положительны.

Условие выполняется, следовательно, система устойчива.

4) Определим устойчивость по критерию Раусса:

Для устойчивости системы необходимо и достаточно, чтобы все коэффициенты первой графы таблицы Раусса были положительны.

№п/п	1 столбец	2 столбец	R
1	160	18,5
2	104	1
3	16,96		1.54

C3.1 = a2 -

Условие выполняется, следовательно, система устойчива.

5) Определим устойчивость по критерию устойчивости Михайлова

Для устойчивости системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов, равное порядку характеристического уравнения, последовательно проходя эти квадранты.

L(p) = 160p³+104p²+18.5p+1 = 0

Заменим р на jw и получим характеристический вектор:

L(jw) = 160(jw)³+104(jw)²+18.5jw+1= 0

Выделим вещественную и мнимые части:

U(w) = 1

jV(w) = 160(jw)³+104(jw)²+18.5jw

Задаваясь значениями w от нуля до бесконечности вычислим U(w) и jV(w). Результаты вычислений занесем в таблицу:

Из годографа Михайлова следует, что система устойчива.

6) Определим устойчивость по критерию устойчивости Евсюкову:

Необходимое условие: , где k₁ = a₁/a₂, k₂ = a₂/a₁, … k_n = k_n/k_n-1

k₁ = 104/160=0.65

k₂ = 18.5/104=0.18

k₃ = 1/18.5=0.054

k_{1 >}k₃

Система устойчива

7) Определим устойчивость по критерию устойчивости Найквиста:

w=tf([1.2],[160 104 18.5 1])

Transfer function:

1.2

------------------------------

160 s^3 + 104 s^2 + 18.5 s + 1

>> nyquist(w)

Годограф Найквиста не охватывает точку (-1;0), следовательно система устойчива.

8) Определим устойчивость по ЛАЧХ и ЛФЧХ:

w=tf([1.2],[160 104 18.5 1])

Transfer function:

1.2

------------------------------

160 s^3 + 104 s^2 + 18.5 s + 1

>> pole(w)

ans =

-0.4000

-0.1250 + 0.0000i

-0.1250 - 0.0000i

>> zero(w)

ans =

Empty matrix: 0-by-1

>> bode(w)

Запас устойчивости по фазе бесконечен.

9) Исследование устойчивости по Шур-Конну:

160p³+104p²+18.5p+1 = 0;

Устойчивость дискретной системы определим по методу Шур-Кона. Согласно этому методу замкнутая система устойчива, если все корни характеристического уравнения лежат внутри круга единичного радиуса. Корни характеристического уравнения будут лежать внутри единичной окружности, если коэффициенты уравнения удовлетворяют определителям Шур-Кона, имеющим значения:, для нечетных , , для четных .

Коэффициенты характеристического уравнения:

а0 = 160; а1 = 104; а2 = 18,5; а3 = 1

Составим и вычислим определители Шур-Кона

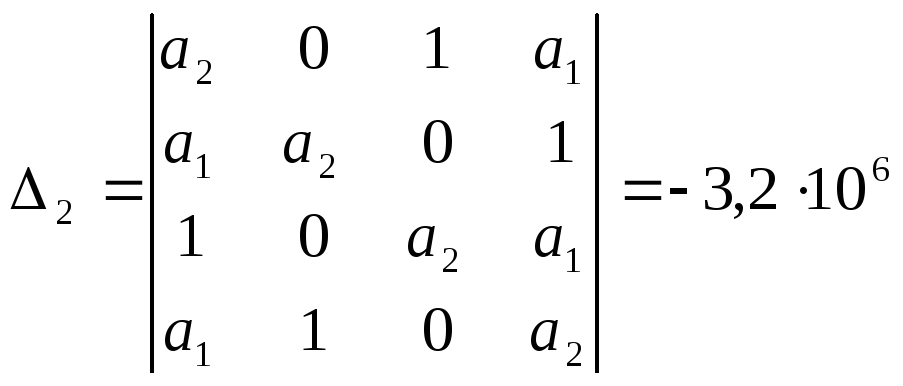
Т.к необходимые условия не выполняются и корни характеристического уравнения лежат не внутри единичной окружности, значит, дискретная замкнутая система не устойчива.

Вывод: В данной работе я изучила методы исследования стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР.