10. Формирования оптимального портфеля ценных бумаг. Модель Тобина. Линия капитала. Свойства т-портфеля.

Ожидаемая доходность портфеля цен­ных бумаг и риск зависят от его структуры, т. е. от доли исход­ного капитала, вложенного в каждую i -ю ценную бумагу. Задача оп­тимизации в системе координат «доходность - риск» заключается в определении такой структуры портфеля, которая обес­печила бы достижение заданной доходности портфеля с мини­мальным риском. Математически задачу оптимизации портфеля ценных бумаг можно записать с помощью системы уравнений

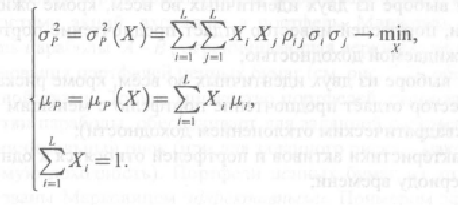
Портфельная теория Марковица получила дальнейшее разви­тие в работах Д. Тобина (удостоен Нобелевской премии в области экономики в 1981 г.). Им были исследованы вопросы оптимизации структуры портфелей при дополнительных предположениях о том, что инвестор имеет возможность совершать операции кредитова­ния и заимствования по единой безрисковой процентной ставке. В состав диверсифицированного портфеля включались уже не толь­ко рисковые ценные бумаги (акции), но и безрисковые активы (на­пример, краткосрочные государственные облигации с фиксирован­ным доходом).

Оптимизация структуры такого комбинированного портфеля требует ответа на три вопроса.

Как новые возможности диверсификации портфеля отражаются на его характеристиках (ожидаемой доходности и риске)?

Какой должна быть структура рисковой части комбинированно­го портфеля?

В каких пропорциях следует распределять денежные средства между рисковой и безрисковой частями портфеля?

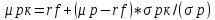
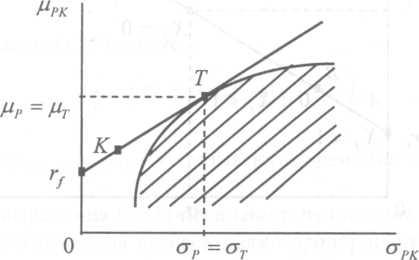
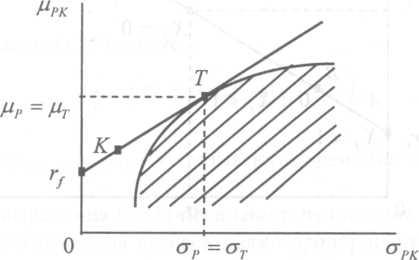
Это выражение показывает, что ожидаемая доходность и риск комбинированного портфеля связаны линейной зависимостью. Эту зависимость принято называть линией капитала. На ней располагается всё множество комбинированных портфелей.

Множество оптимальных, по Тобину, комбинированных порт­фелей ценных бумаг располагается на линии капитала, которая явля­ется касательной к фронту эффективных, по Марковицу, портфелей. Примером оптимального портфеля ценных бумаг является портфель К.

Точка касания Т соответствует ха­рактеристикам рисковой составляющей комбинированного портфе­ля. Структура этого Т -портфеля определяется единственным образом и не зависит ни от ожидаемой доходности комбинированного портфеля, ни от склонности инвестора к риску.

11. Формирования оптимального портфеля ценных бумаг. Модель Шарпа. Рыночная линия капитала. Свойства м-портфеля. Рыночная линия ценной бумаги. Роль коэффициентов «альфа» и «бета». (2 стр.)

Ожидаемая доходность портфеля цен­ных бумаг и риск зависят от его структуры, т. е. от доли исход­ного капитала, вложенного в каждую i -ю ценную бумагу. Задача оп­тимизации в системе координат «доходность - риск» заключается в определении такой структуры портфеля, которая обес­печила бы достижение заданной доходности портфеля с мини­мальным риском. Математически задачу оптимизации портфеля ценных бумаг можно записать с помощью системы уравнений.

Модель У. Шарпа (лауреата Нобелевской премии в области эко­номики в 1990 г.) широко известна как модель оценки долгосрочных активов» (Capital Asset Pricing Model - САРМ).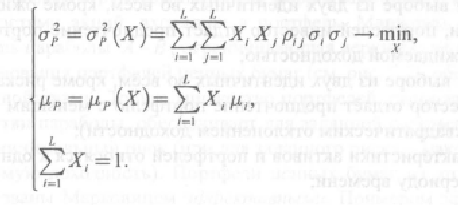

Поскольку САРМ ос­новывается на теории Марковица - Тобина, то исходные допущения для этой модели включают все модельные предположения, сделан­ные Марковицем и Тобиным. Кроме того, Шарп сделал следующие дополнительные предположения относительно использования ин­формации участниками рынка:

1. информация в одинаковой степени доступна всем участникам рынка, которые идентично её интерпретируют и мгновенно исполь­зуют для принятия или корректировки решений. Это обусловливает эффективность рынка ценных бумаг;

2. инвесторы на основе однородных ожиданий имеют одинако­вые прогнозы относительно доходности и риска ценных бумаг.

На эффективном рынке все инвесторы, поступая рационально, стремятся сформировать свои портфели активов оптимальным обра­зом с точки зрения доходности и риска. Они используют одни и те же прогнозные значения характеристик активов (ожидаемых значений до­ходностей, дисперсий и ковариаций).

Следовательно, для всех инвесторов, формирующих комбини­рованные портфели ценных бумаг, оптимальный портфель рисковых ценных бумаг (портфель, структура которого соответствует точке касания линии капитала с фронтом эффективных портфелей) будет одним и тем же. На эффективном рынке таким портфелем может быть только один портфель - рыночный (М-портфель). Рыночный портфель - это совокупность всех рисковых ценных бу­маг, обращающихся на рынке, т. е. рыночный портфель идентичен по своей структуре Т -портфелю (модель Тобина), сформированному в условиях равновесного эффективного рынка. На практике в качест­ве рыночного портфеля используется индексный портфель. В него включают рисковые ценные бумаги, на основе параметров которых формируется ведущий на рынке фондовый индекс.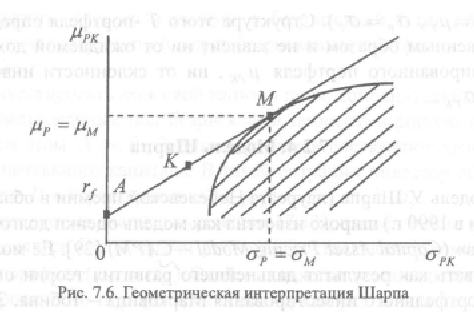

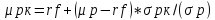
Это выражение показывает, что ожидаемая доходность и риск комбинированного портфеля связаны линейной зависимостью. Эту зависимость принято называть линией капитала. На ней располагается всё множество комбинированных портфелей.

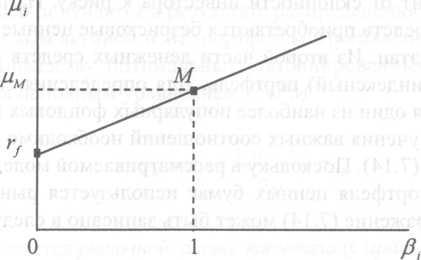
Выражение показывает, что премия за риск при инвести­ровании в любую ценную бумагу, обращающуюся на фондовом рын­ке, равна среднерыночной премии за риск (рассчитываемой по фон­довому индексу), умноженной на коэффициент β соответствующей ценной бумаги.

Выражение представляет собой линейную зависимость μi от β., которую в финансовом анализе называют рыночной линией ценной бумаги (Security Market Line - SML).