8. Диверсификация риска на рынке ценных бумаг. Возможности портфеля ценных бумаг по уменьшению риска инвестора. Влияние корреляции доходностей ценных бумаг на возможность уменьшения риска.

Один из наиболее распространенных способов управления рис­ками - диверсификация вложений. Она осуществляется путём ин­вестирования капитала в различные активы (например, в ценные бумаги нескольких эмитентов), набор которых образует портфель инвестора. Правильное (оптимальное) формирование портфеля во многих случаях позволяет без существенного сокращения доходно­сти уменьшить риск

Эффект от портфельного инвестирования может быть выявлен в результате анализа зависимостей μ_р = μ_р (L) и σ _р = σ (L) при условии неограниченной диверсификации портфеля (L —> оо) и различных предположениях относительно корреляции доходностей ценных бумаг (р _ij = 0, p _ij = 1 и р _ij = -1). Для упрощения анализа целесообразно предположить, что капитал инвестора распределён между активами в равных про­порциях.

Тогда, в первом случае мы имеем, что ожидаемая доходность портфеля равна среднему арифметическому значению ожидаемых доходно­стей ценных бумаг, составляющих данный портфель. Таким образом, при р _ij = 0 диверсификация вложений позволя­ет уменьшить риск инвестора. В этом случае можно достичь ситуа­ции, когда σ p «σ _i

Во втором случае, когда доходности ценных бумаг прямо коррелированны мы имеем, что ожидаемая доходность портфеля считается аналогично предыдущему. Но однако диверсификация портфеля не даёт положи­тельного эффекта. Происходит лишь усреднение рисков вложений в отдельные ценные бумаги.

В третьем случаем доходности ценных бумаг в портфеле имеют отрицательную корреляцию. Тогда мы получаем выражение, согласно которому появляется возможность составление безрискового портфеля. Однако за снижение риска приходится платить некоторым уменьшением доходности.

9. Формирования оптимального портфеля ценных бумаг. Модель Марковица. Фронт эффективных портфелей.

Ожидаемая доходность портфеля цен­ных бумаг и риск зависят от его структуры, т. е. от доли исход­ного капитала, вложенного в каждую i -ю ценную бумагу. Задача оп­тимизации в системе координат «доходность - риск» заключается в определении такой структуры портфеля, которая обес­печила бы достижение заданной доходности портфеля с мини­мальным риском. Математически задачу оптимизации портфеля ценных бумаг можно записать с помощью системы уравнений

При построении своей модели Марковиц сделал определён­ные допущения (модельные предположения) относительно: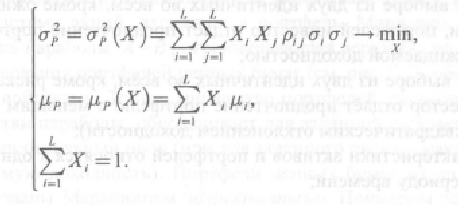

• вероятностной модели доходностей акций

• рынка акций и поведения его участников.

Вероятностная модель. Предполагается, что множество доход­ностей по каждой i -й ценной бумаге, полученное за анализируемый период времени t, можно рассматривать как выборку случайных значений, распределённых по нормальному закону.

Предположения относительно рынка и поведения его участни­ков состоят в следующем:

1. инвесторы оценивают портфели, основываясь на ожидаемой доходности и риске активов;

2. при выборе из двух идентичных во всём, кроме ожидаемой доходности, портфелей инвестор отдаёт предпочтение портфелю с большей ожидаемой доходностью;

3. при выборе из двух идентичных во всём, кроме риска, порт­фелей инвестор отдаёт предпочтение портфелю с меньшим риском (средним квадратическим отклонением доходности);

4. характеристики активов и портфелей относятся к одному за­данному периоду времени

5. активы являются бесконечно делимыми, т. е. в каждый актив может быть вложена любая доля капитала инвестора;

6. отсутствуют какие-либо технические препятствия в реализа­ции оптимальных инвестиционных стратегий; с любым активом воз­можна операция «короткая продажа»; налоги и издержки, связанные с покупкой и продажей активов, не учитываются.

В результате своего исследования Марковиц установил, что для акций с заданными параметрами (см. 7.1.1) в системе коор­динат «доходность - риск» имеется некая область существования портфелей (фрагмент области - заштрихованная часть)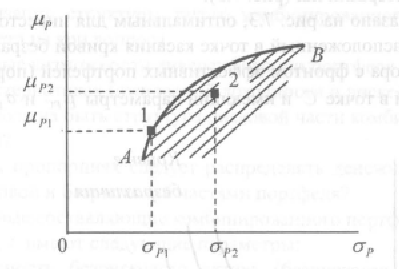

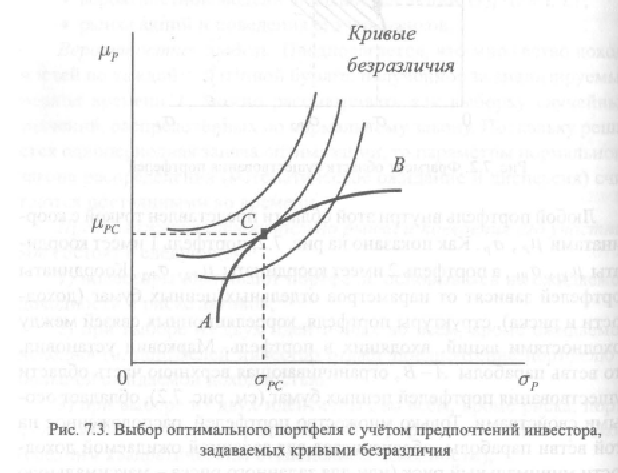
Только множество портфелей, расположенное на ветви параболы А-В, обеспечивает для заданной ожидаемой доход­ности минимальный риск (или для заданного риска - максимальную ожидаемую доходность). Портфели ценных бумаг из этого множе­ства названы Марковицем эффективными. Примером эффективного портфеля является портфель 1