24) Математическая модель равномерного прямолинейного полета самолета:

Линейная математическая модель движения ВС:

где X - вектор состояний размерности n, Ф - переходная матрица системы, определяющая переход из состояния в момент (i-1) в состояние в момент (i); матрицы В' и G'

Математическая модель измерений представляет собой линейную функцию от компонент вектора состояний

где z - вектор измеряемых параметров размером т; С -матрица, устанавливающая связь измерений с элементами вектора состояний, размером (т_п): - нормальный случайный вектор ошибок измерений типа "дискретный белый шум" со статистическими характеристика­ми, аналогичными характеристикам возмущающего воздействия, т.е.

При независимых ошибках - матрица квадратов среднеквадратических ошибок измерений.

Предполагается, что случайные возмущения, ошибки измерения и элементы вектора состоянии некоррелированы, т.е. при любых i,j. В качестве критерия оптимальности опенки состояний принимают минимум среднеквадратической ошибки т.е. минимум суммы среднеквадратических ошибок оценок отдельных составляющих вектора состояний

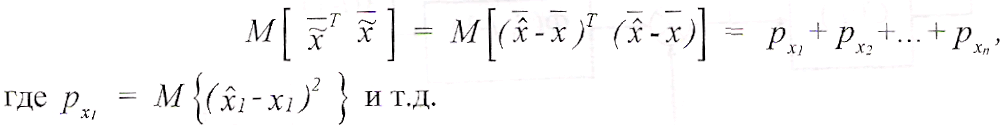
Статистические свойства вектора ошибок оценки характеризуются корреляционной матрицей ошибок оценки

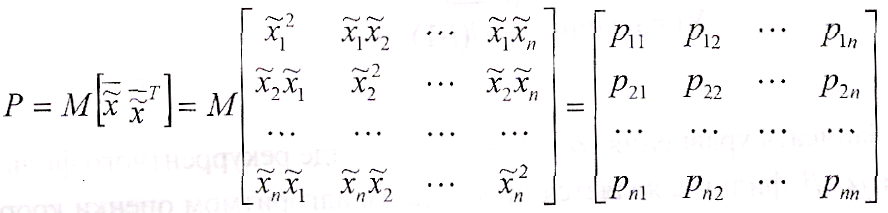
в которой диагональные элементы представляют собой дисперсии ошибок оценок составляющих вектора состояний, т.е.

15. Дискретизация и квантование при первичной обработке рли.

При аналоговой обработке сигналов происходит процесс "свертывания", это происходит за счет использования радиолокационной развертки. (Подается опрный sin & cos? изображается круг), пилообразное напряжение заставляет двигаться луч от центра к краю. В процессе посылки запускающего сигнала и одновременного вращения антенны, зона обнаружения разбивается на элементарные участки по азимуту и по дальности

13. Первичная обработка и задачи обнаружения сигнала.

Задачи:

• обнаружение отраженных сигналов ВС;

• определение координат обнаруженных ВС;

• кодирование координат обнаруженных ВС;

• выделение дополнительной информации, поступающей по вторичному каналу;

• формирование кодограмм сообщений для передачи пользователям.

10. Первичная обработка рлс. Принцип определения дальности и азимута.

11. Первичная обработка рлс. Число импульсов в пачке отраженных сигналов. Минимальный период следования зи.

Характеристики РЛК:

1) Rmax- максимальная дальность на которой безошибочно определяется положение ВС

Rmax=c*PRT/2=c/2PRF PRF=1/PRT – частота

Если известна частота(период следования), то можно Rmax РЛК. Чем больше частота, тем меньше дальность надежность РЛК.

6.Статистические характеристики ошибок измерений рлс в прямоугольной системе координат

Для нахождения статистических характеристик ошибок пересчитанных в прямоугольную систему координат измерений РЛС можно воспользоваться обычным приемом линеаризации, в результате которого получим выражение

где x^* , y^* - пересчитанные в прямоугольную систему координат измерения дальности и азимута; _x , _y - соответствующие случайные ошибки определения прямоугольных координат.

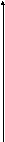
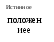
y^*

_

Измерение

y

^*

_y



_

 ^*

Рисунок 1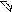

_x

x^*

x

РЛС

Решим эту задачу для координаты x . Запишем связь координаты с измеренными значениями дальности и азимута

Произведем линеаризацию этого выражения путем разложения функции в ряд Тейлора относительно истинных значений  ,  , отбрасывая члены ряда выше первого порядка

Отсюда ошибка определения координаты x равна

Определим дисперсию этой ошибки

Применим операцию математического ожидания к каждому слагаемому, при этом учтем, что поскольку ошибки измерения дальности и азимута независимы, то В результате получим

Аналогично для координаты y :

Обращает внимание тот факт, что дисперсия ошибок определения прямоугольных координат зависит от положения ВС (значений  ,  ), в то время как дисперсии ошибок измерений дальности и угла не изменяются.