- •26. Уравнение α-β фильтра
- •25. Схема алгоритма α-β фильтра
- •27. Схема α-β фильтра
- •28. Дискретный фильтр Калмана. Математическая постановка.
- •29.Структурная схема фильтра Калмана
- •30.Уравнение фильтра Калмана.
- •31.Критерии оценки фильтр Калмана, матрица ковариации ошибок оценки.
- •18. Вторичная обработка рли. Задача обнаружения и сопровождения траекторий. Дать иллюстрирующуй рисунок.
- •1. Основные характеристики рлс:
- •35.Мультирадарная обработка рли. Этапы обработки. Метод мозаичной обработки.
- •36. Мультирадарная обработка рли. Метод весовой обработки.
- •38. Приведение рл данных к единому времени.
- •37. Сбор и приведение рл данных к единой системе координат.
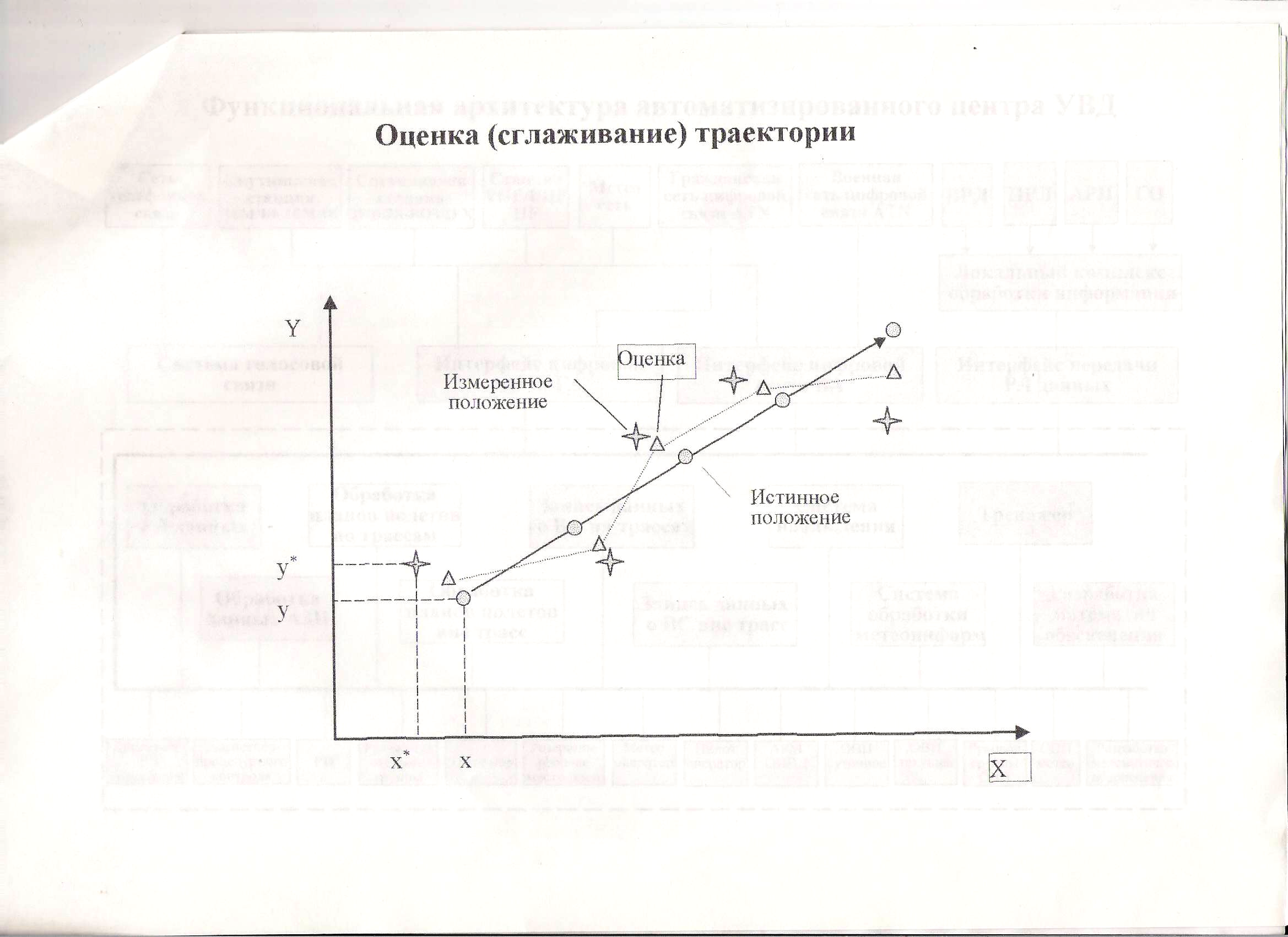
- •21) Задача оценки (сглаживания) траектории полета вс
- •22) Экстраполяция в задаче траекторной оценки и сопровождения вс
- •23) Постановка задачи оценки параметров траектории полета самолета
- •24) Математическая модель равномерного прямолинейного полета самолета:
- •15. Дискретизация и квантование при первичной обработке рли.
- •10. Первичная обработка рлс. Принцип определения дальности и азимута.
- •11. Первичная обработка рлс. Число импульсов в пачке отраженных сигналов. Минимальный период следования зи.
- •6.Статистические характеристики ошибок измерений рлс в прямоугольной системе координат
- •7. Вывод выражения для случайной ошибки определения координаты х, после пересчета измерений из полярной системы координат:
- •8. Вывод выражения для случайной ошибки определения координаты y, после пересчета измерений из полярной системы координат:
- •9. Вывод выражения для дисперсии ошибки определения координаты х, после пересчета измерений рлс из полярной системы координат
- •5. Изучение влияния ошибок рлс на точность и достоверность определения местоположения вс
36. Мультирадарная обработка рли. Метод весовой обработки.
Мультирадарная обработка поступающая от нескольких РЛС (разнесенных друг от друга).
Решаются следующие задачи:
- сбор сообщений поступающих от различных источников информации
- приведение отметок к единой системе координат
- отождествление (сличение) отметок и целей
- осреднение координат нескольких отметок одной цели для получения более точных
координат.
Более сложной является весовая обработка информации, когда координаты определяются с учетом характеристик РЛС. Например, для координаты х
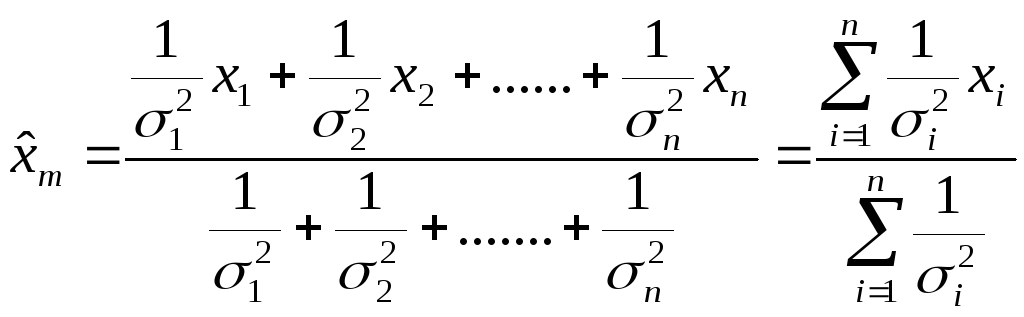
где хi, - результат измерений координаты; σi- среднеквадратическая ошибка измерении i-го радиолокатора.
На первом этапе отождествления производится по парное сравнение координатных и скоростных составляющих. Если сообщение получено от одной и той же цели, то должно выполняться условие
![]()
![]() ~
допустимые
отклонения, определяемые ошибками
оценки и экстраполяции; j,
к
~
допустимые
отклонения, определяемые ошибками
оценки и экстраполяции; j,
к
- номер источника информация; i - номер цели.
38. Приведение рл данных к единому времени.
Для приведения к единому времени принимается модель движения ВС в единой системе координат с постоянной скоростью, т.е.
![]()
где переходная матрица равна
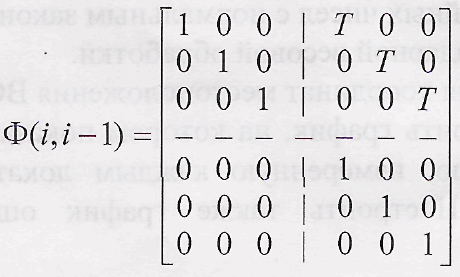
![]()
Приведение
вектора состояний к заданному моменту
времени ts
> ti,
выполняется согласно выражения
![]() для
Т
= ts
-ti
для
Т
= ts
-ti
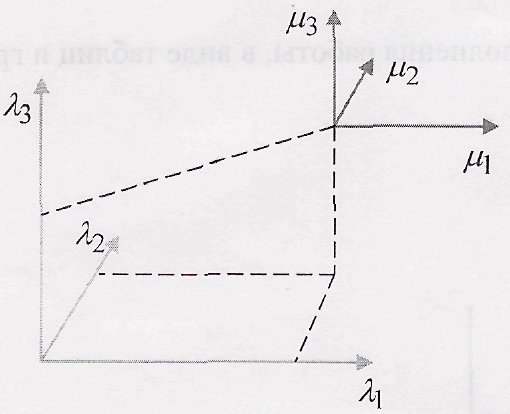
37. Сбор и приведение рл данных к единой системе координат.
При
приведении данных к единой системе
координат решается задача пересчета
из частной радиолокационной системы
координат
![]() в
единую систему координат X.
В
общем виде эта задача решается следующим
образом.
в
единую систему координат X.
В
общем виде эта задача решается следующим
образом.
Пусть
![]() -
вектор координат в частной системе
координат, а
-
вектор координат в частной системе
координат, а
![]() -
вектор
координат в единой системе. Пусть
преобразование вектора
-
вектор
координат в единой системе. Пусть
преобразование вектора
![]() в вектор
в вектор
![]() имеет
вид
имеет
вид
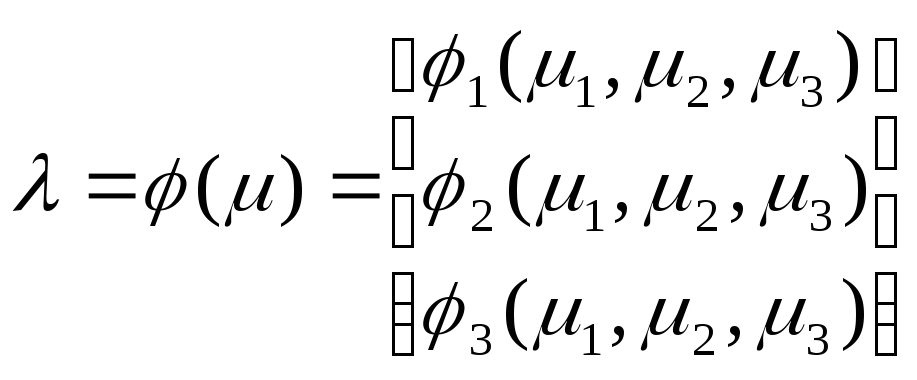
Если
состояние цели характеризуется
координатами и скоростям, то вектор
состояний в частной системе координат
равен
![]() ,
а в единой системе
,
а в единой системе
![]()
Связь
между скоростями определится выражением
![]()
Таким образом, вектор состояний в единой системе координат выражается через вектор состояний час гной системы следующим образом
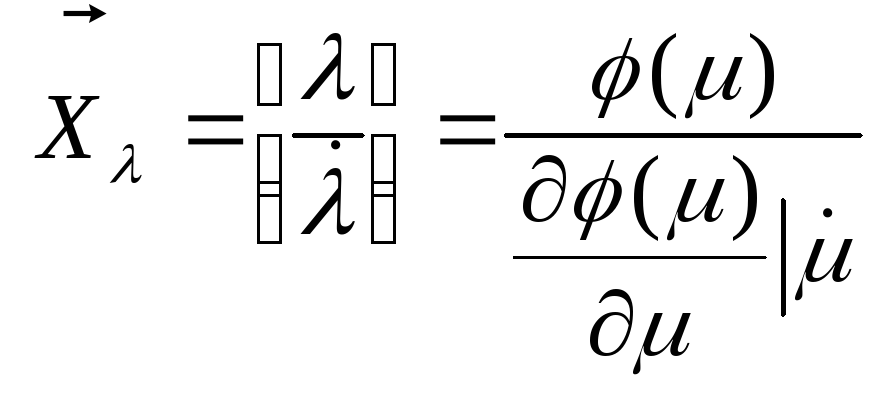
21) Задача оценки (сглаживания) траектории полета вс
Задача оценки параметров траектории движения ВС заключается не только в фильтрации ошибок измерений РЛС и получений более точной оценки местоположения ВС, по и в восстановлении остальных необходимых для процесса управления траекторных параметров, таких как скорость полета, ускорение, курс и другие, которые радиолокатором не измеряются.
Постановка
задачи оценки состояний формулируется
следующим образом. Задана управляемая
система в виде физического соотношения
между вектором состояний х,
управлением
и
и
возмущающим воздействием
![]() .
Задана
также измерительная система в виде
физических соотношений между сигналом
измерений z,
вектором
состояний
.
Задана
также измерительная система в виде
физических соотношений между сигналом
измерений z,
вектором
состояний
![]() и
ошибками измерений
и
ошибками измерений
![]() .
Заданы
статистические характеристики случайных
сигналов
.
Заданы
статистические характеристики случайных
сигналов
![]() и
и
![]() .
Требуется найти оценку состояний
.
Требуется найти оценку состояний
![]() системы
по результатам обработки результатов
измерений
системы
по результатам обработки результатов
измерений
![]() с
ииспользованием
оптимального в заданном смысле
устройства (или алгоритма) оценки,
минимизирующего ошибку оценки
с
ииспользованием
оптимального в заданном смысле
устройства (или алгоритма) оценки,
минимизирующего ошибку оценки
![]()
Оценка
![]() (t
/ Т) должна
удовлетворять определенным критериям
качества. Причем для t
= Т
оценку
называют оценкой фильтрации, для t
< Т -
оценкой сглаживания, а для t
>
Т - оценкой
прогноза.
(t
/ Т) должна
удовлетворять определенным критериям
качества. Причем для t
= Т
оценку
называют оценкой фильтрации, для t
< Т -
оценкой сглаживания, а для t
>
Т - оценкой
прогноза.
Для решения поставленной задачи может быть использован метод Калмана-Бьюси. Дискретный фильтр Калмана дает возможность реализовать оптимальный фильтр в цифровой ЭВМ.