
- •26. Уравнение α-β фильтра
- •25. Схема алгоритма α-β фильтра
- •27. Схема α-β фильтра
- •28. Дискретный фильтр Калмана. Математическая постановка.
- •29.Структурная схема фильтра Калмана
- •30.Уравнение фильтра Калмана.
- •31.Критерии оценки фильтр Калмана, матрица ковариации ошибок оценки.
- •18. Вторичная обработка рли. Задача обнаружения и сопровождения траекторий. Дать иллюстрирующуй рисунок.
- •1. Основные характеристики рлс:
- •35.Мультирадарная обработка рли. Этапы обработки. Метод мозаичной обработки.
- •36. Мультирадарная обработка рли. Метод весовой обработки.
- •38. Приведение рл данных к единому времени.
- •37. Сбор и приведение рл данных к единой системе координат.
- •21) Задача оценки (сглаживания) траектории полета вс
- •22) Экстраполяция в задаче траекторной оценки и сопровождения вс
- •23) Постановка задачи оценки параметров траектории полета самолета
- •24) Математическая модель равномерного прямолинейного полета самолета:
- •15. Дискретизация и квантование при первичной обработке рли.
- •10. Первичная обработка рлс. Принцип определения дальности и азимута.
- •11. Первичная обработка рлс. Число импульсов в пачке отраженных сигналов. Минимальный период следования зи.
- •6.Статистические характеристики ошибок измерений рлс в прямоугольной системе координат
- •7. Вывод выражения для случайной ошибки определения координаты х, после пересчета измерений из полярной системы координат:
- •8. Вывод выражения для случайной ошибки определения координаты y, после пересчета измерений из полярной системы координат:
- •9. Вывод выражения для дисперсии ошибки определения координаты х, после пересчета измерений рлс из полярной системы координат
- •5. Изучение влияния ошибок рлс на точность и достоверность определения местоположения вс
30.Уравнение фильтра Калмана.
Наиболее часто при вторичной обработке РЛИ используется гипотеза о равномерном и прямолинейном полете ВС, которой соответствует полиномиальная модель первой степени. Так для прямоугольной системы координат это будет
![]()
или
в векторно-матричном дискретном виде
записи
![]() где
где
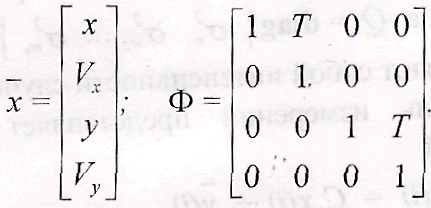
Vх, Vу- проекции скорости; Т = ti -ti-1- период обзора РЛС.
Математически задача восстановления и оценки параметров траектории полета ВС по данным РЛС решается с использованием оптимальных методов опенки состояний динамической системы.
Постановка
задачи оценки состояний формулируется
следующим образом. Задана управляемая
система в виде физического соотношения
между вектором состояний х,
управлением
и
и
возмущающим воздействием
![]() .
Задана
также измерительная система в виде
физических соотношений между сигналом
измерений z,
вектором
состояний
.
Задана
также измерительная система в виде
физических соотношений между сигналом
измерений z,
вектором
состояний
![]() и
ошибками измерений
и
ошибками измерений
![]() .
Заданы
статистические характеристики случайных
сигналов
.
Заданы
статистические характеристики случайных
сигналов
![]() и
и
![]() .
Требуется найти оценку состояний
.
Требуется найти оценку состояний
![]() системы
по результатам обработки результатов
измерений
системы
по результатам обработки результатов
измерений
![]() с
ииспользованием
оптимального в заданном смысле
устройства (или алгоритма) оценки,
минимизирующего ошибку оценки
с
ииспользованием
оптимального в заданном смысле
устройства (или алгоритма) оценки,
минимизирующего ошибку оценки
![]()
Оценка
![]() (t
/ Т) должна
удовлетворять определенным критериям
качества. Причем для t
= Т
оценку
называют оценкой фильтрации, для t
< Т -
оценкой сглаживания, а для t
>
Т - оценкой
прогноза.
(t
/ Т) должна
удовлетворять определенным критериям
качества. Причем для t
= Т
оценку
называют оценкой фильтрации, для t
< Т -
оценкой сглаживания, а для t
>
Т - оценкой
прогноза.
Оцениваемый процесс (вектор состояний) описывают дискретным линейным в общем виде нестационарным уравнением
![]()
где
![]() - вектор
состояний размерностью п:
Ф
- переходная матрица (пхп):
В' -матрица,
распределяющая управления, (пхr);
и - вектор
детермированных управлений размерностью
г;
G'
-
матрица, распределяющая возмущения,
(nxs);
- вектор
состояний размерностью п:
Ф
- переходная матрица (пхп):
В' -матрица,
распределяющая управления, (пхr);
и - вектор
детермированных управлений размерностью
г;
G'
-
матрица, распределяющая возмущения,
(nxs);
![]() -вектор
возмущающих воздействий
размерностью
s
.
-вектор
возмущающих воздействий
размерностью
s
.
Вектор возмущений представляет собой набор случайных некоррелированных между собой процессов типа "дискретный белый шум" .
31.Критерии оценки фильтр Калмана, матрица ковариации ошибок оценки.
В качестве критерия оптимальности оценки состояний принимают минимум среднеквадратической ошибки т.е. минимум суммы среднеквадратических ошибок оценок отдельных составляющих вектора состояний
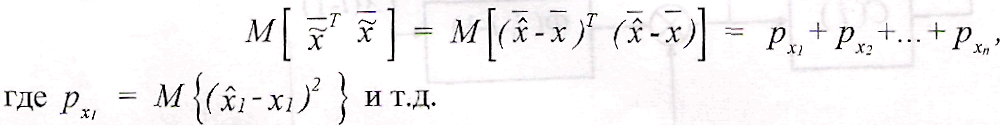

32. Представление α-β фильтра виде рекуррентного фильтра Калмана.
Записать уравнения а-β фильтра в виде рекуррентного фильтра Калмана. При гипотезе о равномерном прямолинейном полете ВС рекуррентная модель движения вдоль координаты х запишется в виде (аналогично для координаты у):
![]()
Если
принять вектор состояний
![]() и
учесть, что скорость полета постоянная,
то можно записать
и
учесть, что скорость полета постоянная,
то можно записать
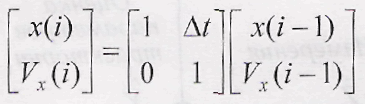
или
![]()
При этом переходная матрица Ф(Δt) определяется непосредственно из математического представления дискретной модели.
Математическая модель измерений координаты х запишется как
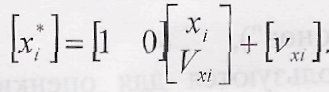
Отсюда
![]()
При
этих условиях матрица коэффициентов
коррекции фильтра Калмана
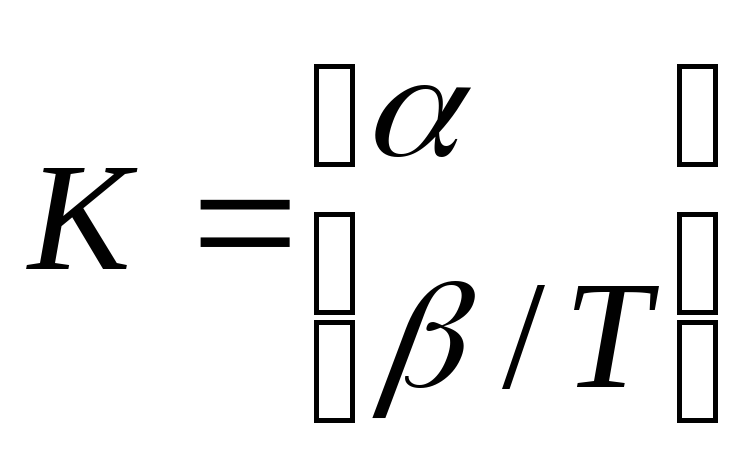 В
результате а-β
фильтр
запишется в пространстве состояний в
общем виде (7.1)
В
результате а-β
фильтр
запишется в пространстве состояний в
общем виде (7.1)
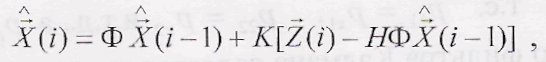
а корреляционная матрица ошибок оценки имеет вид
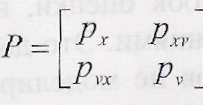
диагональные элементы этой матрицы определяют дисперсию ошибки оценки координаты и скорости, соответственно рх и рv.
