Примеры выполнения заданий Первый семестр

Задание 1.

Вычислить сумму матриц kA+mB, если ,

k=2, m=-3

Решение:

Элементы матрицы суммы определяются по формуле:

c_ij=ka_ij+mb_ij.

Вычислим элементы первой строки матрицы суммы:

с₁₁=2·1+(-3) ·(-1)=5; с₁₂=2·2+(-3) ·6=-14; с₁₃=2·3+(-3) ·(-3)=15.

Аналогично вычисляем остальные элементы:

С₂₁=2·4+(-3) ·0=8; с₂₂=2·5+(-3) ·2=4; с₂₃=2·6+(-3) ·(-5)=27.

С₃₁=2·7+(-3) ·1=11; с₃₂=2·8+(-3) ·10=-14; с₃₃=2·9+(-3) ·7=-9.

Таким образом, матрица суммы примет вид:

Задание 2.

Вычислить определитель третьего порядка

Решение:

Определителем третьего порядка матрицы

называется число, которое определяется следующим образом:

Для вычисления определителей третьего порядка удобно пользоваться правилом треугольников:

Используя правило треугольников, вычислим определитель:

Задание 3.

Решить систему линейных уравнений методом Гаусса.

Решение:

Составляем расширенную матрицу системы, в которую входят коэффициенты при переменных и свободные члены:

Чтобы исключить переменную из второго и третьего уравнений, умножим первую строку на (-2) и (-3) и полученные строки прибавим ко второй и третьей строке соответственно:

Чтобы исключить переменную из третьего уравнения, умножим вторую строку на (-1) и полученную строку прибавим к третьей строке:

Получили систему уравнений, равносильную исходной системе, в которой первое уравнение содержит три переменных, второе – две, а третье – одну переменную:

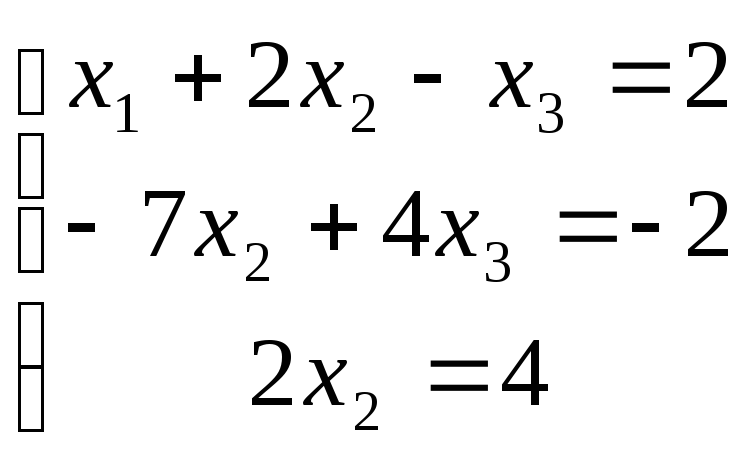
Отсюда последовательно находим:

Таким образом, решение системы:

.

Проверяем полученное решение, подставляя найденные значения в исходную систему:

Получили тождественные равенства, следовательно, система решена правильно.

Задание 4.

Найти косинус угла между векторами и , если А (3; 2; 3), если В(5; 1; 1) и С(1;- 2; -1).

Решение:

По координатам концов найдем эти векторы

,

Отсюда

Найдем скалярное произведение

Применяя теперь формулу, получим

Задание 5.

Вычислить объем тетраэдра АВСD и его высоту DH, если А(0;-3;1);

В(-4;1;2); С(2;-1;5) и D(3;1;-4)

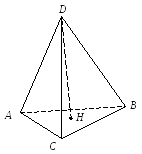
Решение:

Объем тетраэдра (с учетом знака), вершины которого находятся в точках А, В, С и D равен:

. Вычислим объем тетраэдра АВСD:

(определитель раскрыли по первой строке)

С другой, стороны объем тетраэдра равен . Откуда высота равна: . В основании лежит треугольник АВС, площадь которого определяется как модуль векторного произведения векторов и : .

Векторное произведение векторов равно:

. Тогда площадь основания и высота тетраэдра .

Задание 6.

Написать уравнение плоскости, проходящей через точку А и перпендикулярно вектору , если М₁ (0;-1; 3), М₂ (6;4;3), М₃ (-1;0;2).

Решение:

Найдем координаты вектора нормали к плоскости

Уравнение плоскости, проходящей через точку перпендикулярно вектору , где А, В, С – координаты вектора нормали: . В нашем случае А=-7; В=-4; С=-1, тогда уравнение плоскости примет вид:

Задание 7.

Вычислить угол между плоскостями A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0, если А₁=1; В₁=2; С₁=3; D₁=4; А₂=5; В₂=6; С₂=7; D₂=8.

Решение:

Угол между двумя плоскостями определяется по формуле:

Таким образом, получаем .

Тогда угол между плоскостями равен: .