«МАТЕМАТИКА» С.Н. Петрова, Н.В.Коржавина
Уральский государственный экономический университет
Центр дистанционного обучения
Обучающий модуль по дисциплине «математика»
Для организации самостоятельной работы студентов
I блок – информационный
Курс «Математика» является обязательным в цикле естественнонаучных дисциплин Федерального компонента государственного образовательного стандарта высшего профессионального образования.
Основные положения дисциплины «Математика» являются фундаментом математического образования дипломированного специалиста, имеющим важное значение для успешного изучения специальных дисциплин, которые предусмотрены учебной программой для каждой специальности.
Для эффективного усвоения учебного материала и получения итоговой аттестации необходимо в сроки, предусмотренные учебным планом, выполнить практические и контрольные задания и предоставить их для проверки преподавателю по электронной почте (в системе e-Learning.usue.ru).
График самостоятельной работы по изучению теоретического материала; выполнению практических и контрольных заданий по дисциплине приведен в Таблице 1.
Таблица 1.
График самостоятельной работы по дисциплине «Математика»
|
Содержание |
Сроки сдачи |
Критерии оценки |
|
1.Изучение теоретического материала (учебно-методический комплекс) |
|
|
|
2.Выполнение практических заданий |
за 1,5 месяца до сессии |
Каждое задание оценивается от одного до пяти баллов |
|
3.Решение контрольных работ (подробные рекомендации по выполнению и оформлению контрольных работ см. в УМК по математике) |
за 1 месяц до сессии |
Переаттестация – 20 баллов; Контрольная работа № 1 – 50 баллов; Контрольная работа № 2 – 50 баллов. |
|
4. Подготовка к итоговой аттестации |
во время сессии |
|
К сессии Вам необходимо изучить теоретический материал и выполнить все практические задания в соответствии с графиком изучения и отчетности по дисциплине; предоставить все материалы для проверки преподавателю в указанные сроки. Баллы, полученные за выполнение практических и контрольных работ, будут учитываться при итоговой аттестации.
II блок – методический
Для получения итоговой аттестации по дисциплине студент в течение семестра должен выполнить практические задания. Выбор варианта производится по начальной букве фамилии студента:
|
Начальная буква фамилии студента |
Вариант |
|
А, Б |
1 |
|
В, Г |
2 |
|
Д, Е, Ж |
3 |
|
З, И, К |
4 |
|
Л, М |
5 |
|
Н, О, П |
6 |
|
Р, С |
7 |
|
Т, У, Ф, Х |
8 |
|
Ц, Ч, Ш, Щ |
9 |
|
Э, Ю, Я |
10 |
Задания для практических работ Первый семестр
Задание 1. (2 балла)
Вычислить
сумму матриц kA+mB,
если
,
|
Вариант |
k |
m |
Вариант |
k |
m |
|
1 |
4 |
-2 |
6 |
6 |
-3 |
|
2 |
6 |
-1 |
7 |
-4 |
5 |
|
3 |
5 |
3 |
8 |
-6 |
3 |
|
4 |
-3 |
8 |
9 |
7 |
-2 |
|
5 |
4 |
2 |
10 |
9 |
3 |
Пример решения
Задание 2. (3 балла)
Вычислить определитель третьего порядка:
|
Вариант 1 |
|
Вариант 6 |
|
|
Вариант 2 |
|
Вариант 7 |
|
|
Вариант 3 |
|
Вариант 8 |
|
|
Вариант 4 |
|
Вариант 9 |
|
|
Вариант 5 |
|
Вариант 10 |
|
Пример решения
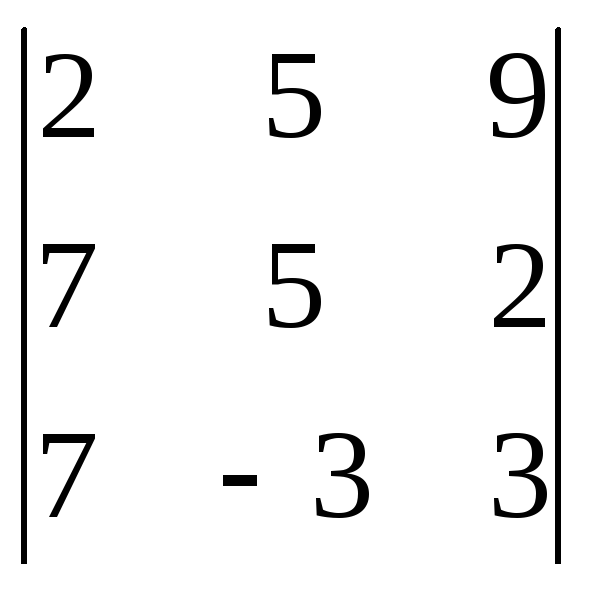
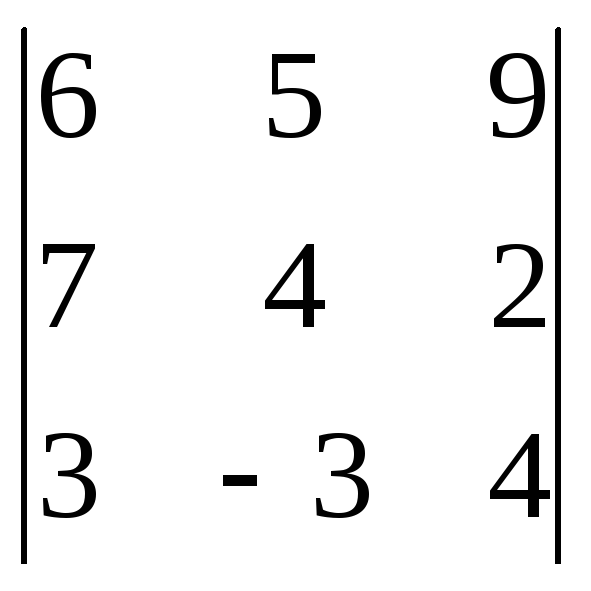
Задание 3. (5 баллов)
Решить систему линейных уравнений методом Гаусса:
|
Вариант 1 |
|
Вариант 6 |
|
|
Вариант 2 |
|
Вариант 7 |
|
|
Вариант 3 |
|
Вариант 8 |
|
|
Вариант 4 |
|
Вариант 9 |
|
|
Вариант 5 |
|
Вариант 10 |
|
Пример решения
Задание 4. (3 балла)
Найти
косинус угла между векторами
и
:
|
№ варианта |
Точка А |
Точка В |
Точка С |
||||||
|
x1 |
y1 |
z1 |
x2 |
y2 |
z2 |
x3 |
y3 |
z3 |
|
|
1 |
2 |
-3 |
5 |
9 |
5 |
-3 |
4 |
7 |
2 |
|
2 |
9 |
6 |
4 |
-3 |
6 |
0 |
-5 |
10 |
1 |
|
3 |
-1 |
6 |
0 |
3 |
-6 |
2 |
6 |
3 |
8 |
|
4 |
6 |
-1 |
3 |
4 |
5 |
-1 |
4 |
0 |
7 |
|
5 |
2 |
-1 |
5 |
6 |
1 |
4 |
7 |
0 |
2 |
|
6 |
3 |
2 |
-4 |
4 |
3 |
9 |
9 |
-3 |
7 |
|
7 |
5 |
4 |
-7 |
2 |
2 |
-4 |
-6 |
7 |
2 |
|
8 |
6 |
8 |
-4 |
4 |
1 |
10 |
9 |
3 |
6 |
|
9 |
7 |
5 |
7 |
7 |
7 |
2 |
6 |
1 |
8 |
|
10 |
3 |
4 |
2 |
0 |
2 |
6 |
0 |
3 |
9 |
Пример решения
Задание 5. (5 баллов)
Вычислить объем тетраэдра АВСD и его высоту DH:
|
№ вар. |
Точка А |
Точка В |
Точка С |
Точка D |
||||||||
|
1 |
x1 |
y1 |
z1 |
x2 |
y2 |
z2 |
x3 |
y3 |
z3 |
x4 |
y4 |
z4 |
|
2 |
1 |
5 |
2 |
-3 |
5 |
9 |
5 |
-3 |
4 |
7 |
2 |
1 |
|
3 |
3 |
6 |
9 |
6 |
4 |
-3 |
6 |
0 |
-5 |
10 |
1 |
2 |
|
4 |
4 |
7 |
-1 |
6 |
0 |
3 |
-6 |
2 |
6 |
3 |
8 |
3 |
|
5 |
2 |
7 |
6 |
-1 |
3 |
4 |
5 |
-1 |
4 |
0 |
7 |
4 |
|
6 |
9 |
5 |
2 |
-1 |
5 |
6 |
1 |
4 |
7 |
0 |
2 |
5 |
|
7 |
1 |
0 |
3 |
2 |
-4 |
4 |
3 |
9 |
9 |
-3 |
7 |
6 |
|
8 |
3 |
2 |
5 |
4 |
-7 |
2 |
2 |
-4 |
-6 |
7 |
2 |
7 |
|
9 |
6 |
1 |
6 |
8 |
-4 |
4 |
1 |
10 |
9 |
3 |
6 |
8 |
|
10 |
8 |
7 |
7 |
5 |
7 |
7 |
7 |
2 |
6 |
1 |
8 |
9 |
Пример решения
Задание 6. (4 балла)
Написать
уравнение плоскости, проходящей через
точку М1
и перпендикулярно вектору
:
|
№ варианта |
Точка М1 |
Точка М2 |
Точка М3 |
||||||
|
x1 |
y1 |
z1 |
x2 |
y2 |
z2 |
x3 |
y3 |
z3 |
|
|
1 |
2 |
-3 |
7 |
9 |
5 |
-3 |
4 |
4 |
2 |
|
2 |
9 |
6 |
10 |
-3 |
4 |
0 |
-5 |
1 |
1 |
|
3 |
-1 |
6 |
3 |
3 |
0 |
2 |
6 |
8 |
8 |
|
4 |
6 |
-1 |
0 |
4 |
3 |
-1 |
4 |
4 |
7 |
|
5 |
2 |
-1 |
0 |
6 |
5 |
4 |
7 |
9 |
2 |
|
6 |
3 |
2 |
-3 |
4 |
-4 |
9 |
9 |
0 |
7 |
|
7 |
5 |
4 |
7 |
2 |
-7 |
-4 |
-6 |
3 |
2 |
|
8 |
6 |
8 |
3 |
4 |
-4 |
10 |
9 |
0 |
6 |
|
9 |
7 |
5 |
1 |
7 |
7 |
2 |
6 |
2 |
8 |
|
10 |
3 |
4 |
3 |
0 |
2 |
6 |
0 |
1 |
9 |
Пример решения
Задание 7. (3 балла)
Вычислить угол между плоскостями A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0:
|
№ варианта |
A1 |
B1 |
C1 |
D1 |
A2 |
B2 |
C2 |
D2 |
|
1 |
2 |
-3 |
7 |
9 |
5 |
-3 |
4 |
4 |
|
2 |
9 |
6 |
10 |
-3 |
4 |
0 |
-5 |
1 |
|
3 |
-1 |
6 |
3 |
3 |
0 |
2 |
6 |
8 |
|
4 |
6 |
-1 |
0 |
4 |
3 |
-1 |
4 |
4 |
|
5 |
2 |
-1 |
0 |
6 |
5 |
4 |
7 |
9 |
|
6 |
3 |
2 |
-3 |
4 |
-4 |
9 |
9 |
0 |
|
7 |
5 |
4 |
7 |
2 |
-7 |
-4 |
-6 |
3 |
|
8 |
6 |
8 |
3 |
4 |
-4 |
10 |
9 |
0 |
|
9 |
7 |
5 |
1 |
7 |
7 |
2 |
6 |
2 |
|
10 |
3 |
4 |
3 |
0 |
2 |
6 |
0 |
1 |
Пример решения