Числовые ряды и их свойства.

Числовой ряд – это сумма бесконечного количества чисел, выбранных по определенному алгоритму. Обычно задают формулу общего члена ряда .

Примеры

1. 1+- бесконечно убывающая геометрическая прогрессия со знаменателем . Ее сумма равна ,

2. 1+1+1+…..Сумма этого ряда бесконечна.

3. 1-1+1-1… Сумма этого ряда не существует (ни конечная, ни бесконечная).

При изучении рядов возникает основной вопрос: «Сходится ли ряд». Отвечая на этот вопрос для геометрической прогрессии, мы вычисляем последовательно 1+, =1+ 1+ - суммы n членов ряда – частичные суммы ряда .

Ряд называется сходящимся, если существует конечный предел последовательности частичных сумм ряда – он называется суммой ряда .

Ряд называется расходящимся, если предел частичных сумм ряда бесконечен или вообще не существует.

Необходимый признак сходимости ряда. Если ряд сходится, то .

Доказательство. . Пусть ряд сходится, тогда .

Необходимый признак позволяет отсеивать часть расходящихся рядов.

Признаки сравнения рядов.

Первый признак сравнения рядов.

Пусть выполнено неравенство . Тогда из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Замечание. В силу свойства сходящихся рядов, конечное число членов ряда не влияет на сходимость и неравенство можно проверять «начиная с некоторого n». Поэтому эту фразу часто можно встретить в теоремах о рядах. Иногда ее просто опускают, но ее всегда надо иметь в виду.

Доказательство. 1) Пусть ряд сходится. Тогда выполнено неравенство . Поэтому последовательность частичных сумм ограничена сверху числом . Но эта последовательность не убывает. Следовательно, по теореме Вейерштрасса . Последнее неравенство справедливо в силу теоремы о предельном переходе в неравенстве.

2) Пусть ряд расходится. Если ряд сходится, то по п.1 доказательства и ряд сходится. Противоречие. Следовательно, ряд расходится.

Пример. Ряд расходится, так как , а ряд (гармонический) расходится.

Второй признак сравнения.

Пусть . Тогда ряды и сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится.

Доказательство. Раскроем определение предела. .

.

Если ряд сходится, то по 1 признаку сравнения ряд сходится (, ряд сходится (свойство сходящихся рядов).

Если ряд сходится, то ряд сходится (свойство сходящихся рядов), тогда по 1 признаку сравнения ряд сходится.

Пусть ряд расходится. Если ряд сходится, то по предыдущему ряд сходится (противоречие).

Пусть ряд расходится. Если ряд сходится, то по предыдущему ряд сходится (противоречие).

Пример. Ряд с расходится по второму признаку сравнения (ряд сравнения – гармонический ряд).

Ряд 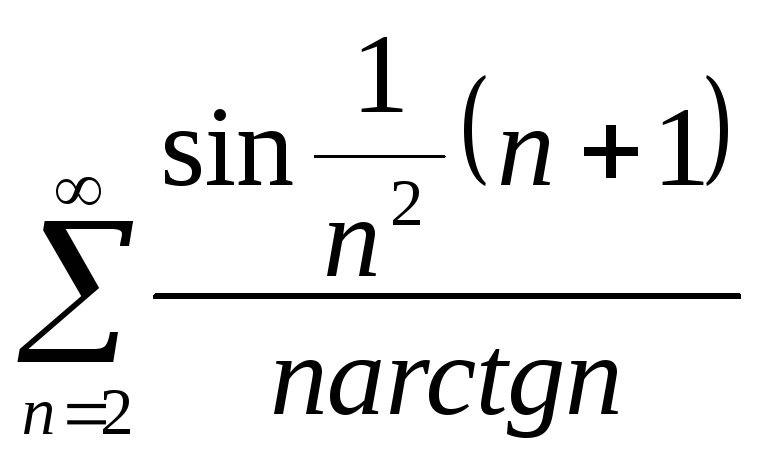сходится. - ограничена. Ряд сравнения - сходящийся ряд Дирихле.

Признак Даламбера.

Конечная форма признака Даламбера.

Пусть , тогда ряд сходится.

Пусть , тогда ряд расходится.

Доказательство. Пусть .

Тогда .

, и ряд сходится. Можно было, не оценивая частичную сумму ряда, заключить, что ряд сходится по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.

Пусть , Тогда . Поэтому не стремится к нулю при , необходимый признак сходимости ряда не выполнен, ряд расходится.

Предельная форма признака Даламбера.

Пусть , тогда ряд сходится. Пусть , тогда ряд расходится. Если , то признак не позволяет сделать вывод о сходимости или расходимости ряда.

Доказательство. Пусть . Тогда .

При малом . По конечной форме признака Даламбера ряд сходится.

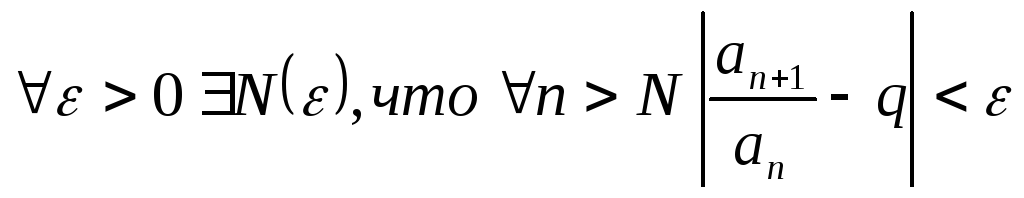Пусть . Тогда . При малом , то есть . Поэтому не стремится к нулю при , необходимый признак сходимости ряда не выполнен, ряд расходится.

Замечание. Признак Даламбера удобно применять, когда общий член ряда содержит произведение некоторых чисел или факториал.

Правда, если общий член ряда содержит факториал, то его можно заменить по формуле Стирлинга и применять второй признак сравнения.

Пример. .

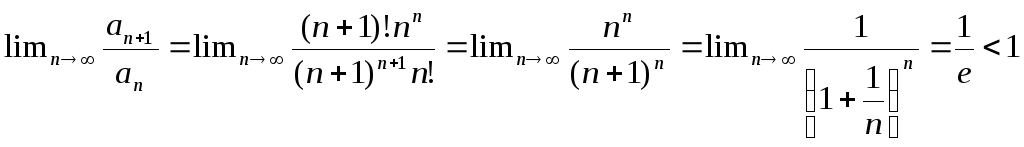. Ряд сходится по признаку Даламбера.

Пример. . Рассмотрим , так как последовательность , монотонно возрастая, стремится к при , то

. Следовательно, . Поэтому не стремится к нулю при , необходимый признак сходимости ряда не выполнен, ряд расходится.

Заметим, что . Поэтому признак Даламбера в предельной форме не дает ответ о сходимости или расходимости ряда, хотя признак в конечной форме позволяет установить расходимость ряда.

Радикальный признак Коши.

Конечная форма радикального признака Коши.

Пусть , тогда ряд сходится.

Пусть , тогда ряд расходится.

Доказательство. Пусть . Тогда , рядсходится по первому признаку сравнения с бесконечно убывающей геометрической прогрессией.

Пусть . Тогда , ряд расходится, так как необходимый признак сходимости ряда не выполнен.

Предельная форма радикального признака Коши.

Пусть , тогда ряд сходится.

Пусть , тогда ряд расходится.

Доказательство. Пусть , тогда .

при малом . Ряд сходится по конечной форме радикального признака Коши.

Пусть , тогда . при малом . Тогда , ряд расходится, так как необходимый признак сходимости ряда не выполнен.

Пример.

, ряд сходится по радикальному признаку Коши в предельной форме.

Замечание. У каждого признака сходимости есть своя «зона нечувствительности». Ни признак Даламбера, ни радикальный признак Коши не позволяют установить расходимость гармонического ряда. Проверьте это. Гармонический ряд расходится, но расходится так слабо, что попадает в «зону нечувствительности» указанных признаков. Интегральный признак Коши имеет меньшую «зону нечувствительности» и позволяет установить расходимость гармонического ряда.

Теорема Дирихле о возможности перестановки местами членов ряда в сходящихся знакоположительных рядах.

Пусть - сходящийся знакоположительный ряд. Тогда его члены можно переставлять, менять местами, полученный ряд будет сходиться и иметь ту же сумму.

Доказательство. Проведем доказательство по индукции.

Пусть меняются местами два члена ряда . Тогда в исходном и полученном перестановкой членов ряде частичные суммы, начиная с будут совпадать. Следовательно, ряд, полученный перестановкой двух членов ряда, , будет сходиться и иметь ту же сумму.

Пусть при перестановке местами членов ряда ряд сходится и имеет ту же сумму.

Пусть переставляются членов ряда. Эта перестановка сводится к перестановке членов ряда, а затем к перестановке еще какого-либо члена с каким-либо другим (перестановке двух членов ряда).

По индуктивному предположению при перестановке местами членов ряда ряд сходится и имеет ту же сумму. Ряд, полученный перестановкой двух членов ряда, будет сходиться и иметь ту же сумму. Следовательно, и при перестановке членов ряда ряд будет сходиться и иметь ту же сумму.