Министерство образования Российской Федерации

Омский государственный технический университет

ТИПОВОЙ РАСЧЕТ И

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

ПО ВЕКТОРНОЙ АЛГЕБРЕ

Для студентов дневного отделения

Омск – 2003

Составители:

Веснина Алла Александровна, доцент

Котюргина Александра Станиславовна, доцент

Занятие 1 Линейные операции над векторами. Линейная зависимость векторов

Определение 1. Геометрическим вектором, или просто вектором, называется направленный отрезок.

Будем обозначать вектор либо как направленный отрезок символом , где точки А и В - начало и конец данного вектора, либо . Начало вектора называют точкой его приложения.

Определение 2. Вектор называется нулевым, если начало и конец его совпадают.

Нулевой вектор не имеет определенного направления и имеет длину, равную нулю. Это позволяет при записи отождествлять нулевой вектор с вещественным числом нуль.

Определение 3. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых.

Определение 4. Три вектора называются компланарными, если они лежат в одной плоскости.

Определение 5. Два вектора называются равными, если они коллиннеарны, имеют одинаковую длину и одинаковое направление.

Все нулевые векторы считаются равными.

Определение 6. Суммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что вектор приложен к концу вектора .

Определение 7. Разностью вектора и вектора называется такой вектор , который в сумме с вектором дает вектор .

Определение 8. Произведением вектора на действительное число называется вектор , коллинеарный вектору , имеющий длину, равную , и имеющий направление, совпадающее с направлением вектора при и противоположное направлению вектора при .

Обозначим буквами основания перпендикуляров, опущенных на ось из точек А и В соответственно.

В

А

Определение 9. Проекцией вектора на ось называется величина

направленного отрезка оси и обозначается . , где - угол между вектором и осью .

Любой вектор может быть разложен по декартову прямоугольному базису : .

Числа - называется декартовыми прямоугольными координатами вектора . Обозначим буквами углы наклона вектора к осям координат; называются направляющими косинусами вектора .

Длина вектора через его координаты имеет вид .

Направляющие косинусы вектора вычисляются по формулам:

; ; ,

откуда следует .

Определение 10. Ортом вектора называется вектор , удовлетворяющий условиям:

1) коллинеарен вектору ,

2) .

Координатами орта вектора являются направляющие косинуса.

Если два вектора заданы в декартовых прямоугольных координат ,,то

.

Условие коллинеарности векторов имеет вид .

Примеры решения задач

Задача 1. В равнобедренной трапеции ОАСВ угол ,,

- середина сторон ВС и АС. Выразить векторы через - единичные векторы направлений .

В М С

N

O A

Решение. . Так как . Найдем

вектор . Из треугольника ОСА , а так как , а

, вектор . Найдем из треуголь-

ника ONC , а так как , , .

Из треугольника OMN .

Задача 2. Даны векторы и , приложены к общей точке. Найти орт биссектрисы угла между .

Решение. Диагональ четырехугольника совпадает с биссектрисой, если этот четырехугольник – ромб (квадрат). Найдя , получим угол с одинаковыми по длине сторонами, равными единице. Таким образом, вектор направлен по биссектрисе угла между .

, ,

.

Найдем длину вектора , тогда орт биссектрисы равен .

Задача 3. Разложить вектор по трем некомпланарным векторам: .

Решение. . .

Приравняем коэффициенты справа и слева:

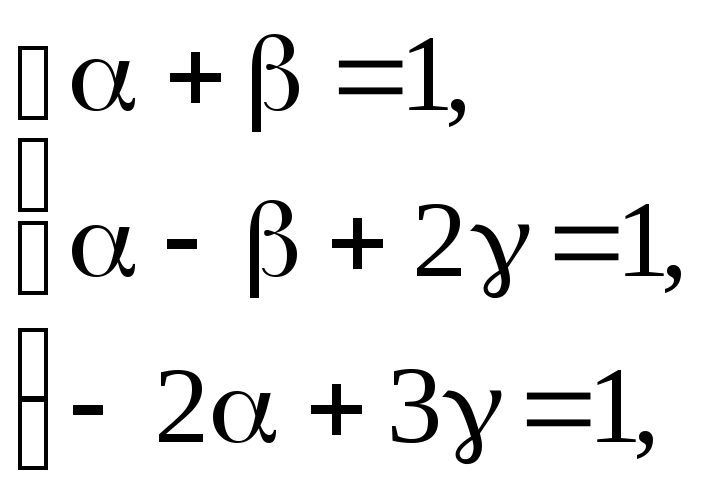тогда и .

Задачи

1. Построить вектор по данным векторам .

2. В треугольнике ОАВ даны векторы . Найти векторы , где М – середина стороны АВ.

3. Пользуясь параллелограммом, построенным на векторах , проверить на чертеже справедливость тождества .

4. В равнобочной трапеции АВСD известно нижнее основание , боковая

сторона и угол между ними . Разложить по все векторы,

составляющие остальные стороны и диагонали трапеции.

5. Даны модуль вектора и углы . Вычислить проекции вектора на координатные оси.

6. Вычислить направляющие косинусы вектора .

7. Вектор составляет с осями ОХ и OZ углы и . Какой угол он

составляет с осью OY?

8. Даны . Найти .

9. Даны . Вычислить .

10. Векторы образуют угол , причем . Определить .

11. Даны четыре вектора: . Определить разложение каждого из этих четырех векторов, принимая в качестве базиса три остальных.

12. Даны точки . Проверить, что векторы коллинеарны; установить, какой из них длиннее другого и во сколько раз, как они направлены – в одну сторону или в противоположные.

13. Найти орт вектора .

14. Два вектора приложены к одной точке. Определить координаты вектора , направленного по биссектрисе угла между векторами и , при условии, что .

15. Исследовать на линейную зависимость систему векторов

.

16. Доказать, что векторы линейно независимы и разложить по ним вектор .