1. Производственная функция.

Технологическая связь между выпуском продукции (результатом) и затратами ресурсов называется производственной функцией вида:

Производственные функции подразделяются на функции с взаимозаменяемыми ресурсами и взаимодополняемыми ресурсами.

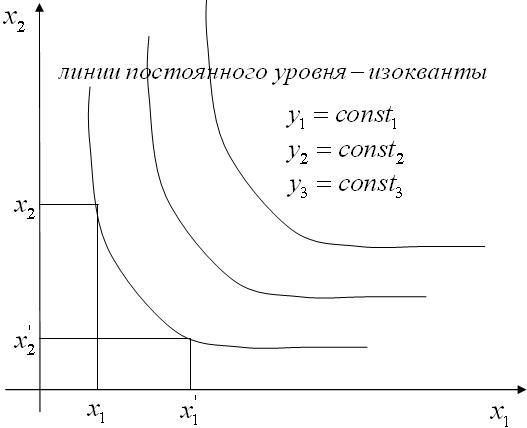
Рассмотрим производственную функцию с взаимозаменяемыми ресурсами. Если ресурсы взаимозаменяемые, то при разных уровнях затрат ресурсов, выпуск продукции может оставаться на постоянном уровне.

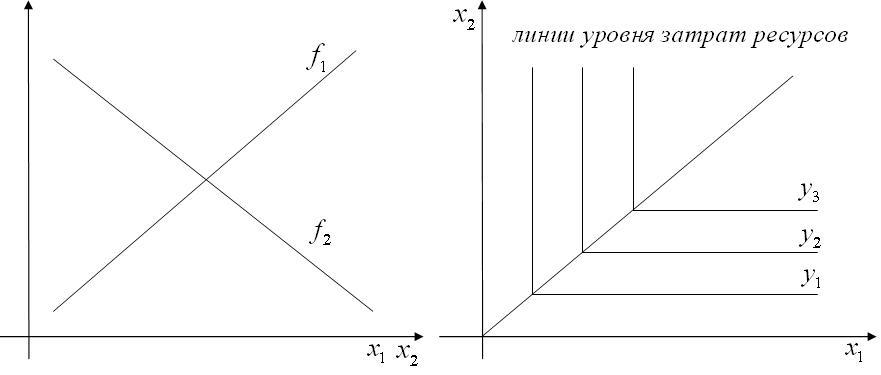
Производственная функция с взаимнодополняемыми ресурсами характеризуется тем, что здесь ресурсы не взаимозаменяются.

- производственная функция для такого случая.

– объём выпуска продукции, при условии, что ресурса j, а остальных ресурсов достаточно (узкое место).

Рассмотрим производственную функцию для двух факторов.

Производственная функция имеет следующие свойства:

1)

2)

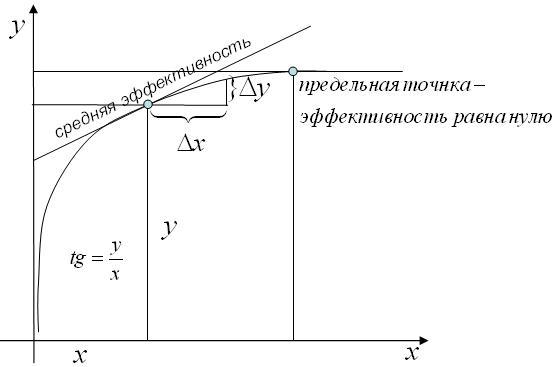
3) эффективность затрат ресурсов (ЭЗР). Среднее ЭЗР определяется:

4) предельная эффективность затрат ресурсов (то есть ЭЗР в данной точке):

5) экономическая область производства определяется вектором:

- экономическая область производства

6) связано с законом убывающей отдачи.

Закон убывающей отдачи гласит, что вторая производная от производственной функции отрицательная, т.е. с ростом затрат ресурсов отдача убывает.

Производственная функция (конспект кафедры).

Предположим, что компания производит один вид товарной продукции и использует n видов ресурсов. Технологическая связь между выпуском товарной продукции и затратами описывается производственной функцией вида:

Если смотреть на производственную функцию как на уравнение регрессии, то можно записать два варианта:

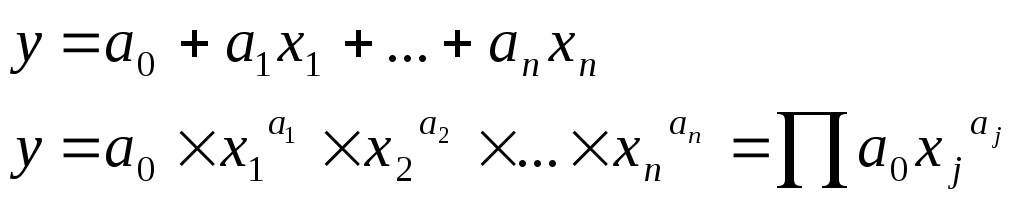
Свойства производственной функции:

если

если

Множество точек, удовлетворяющих уравнению постоянного выпуска, называются изоквантой (определяется взаимозаменяемость ресурсов).

Функция Коба-Дугласа

К – основные производственные фонды

L – численность.

Для характеристики эффективности производственных ресурсов применяются два основных показателя:

• средняя эффективность ресурса:

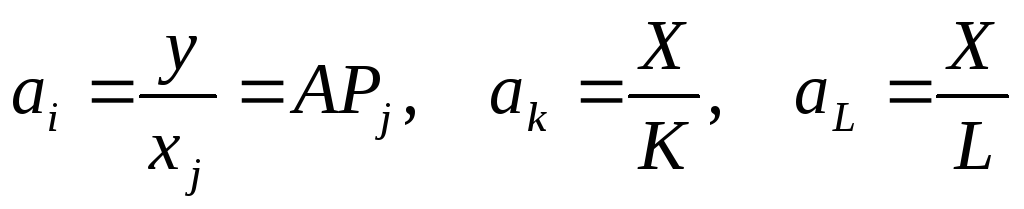
• предельная эффективность ресурса:

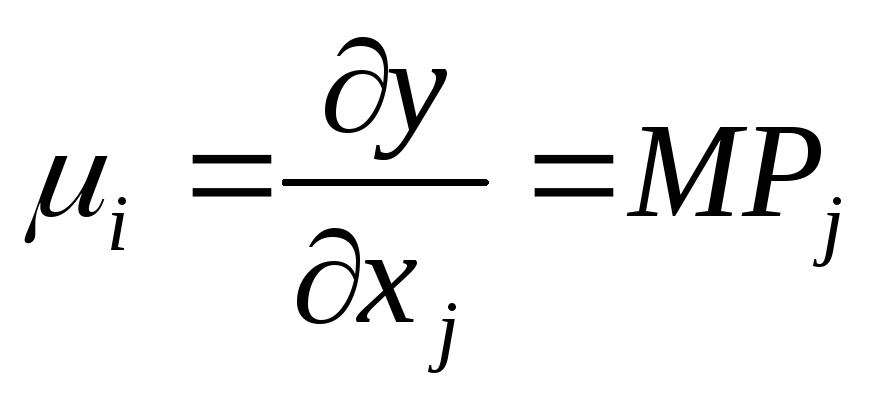
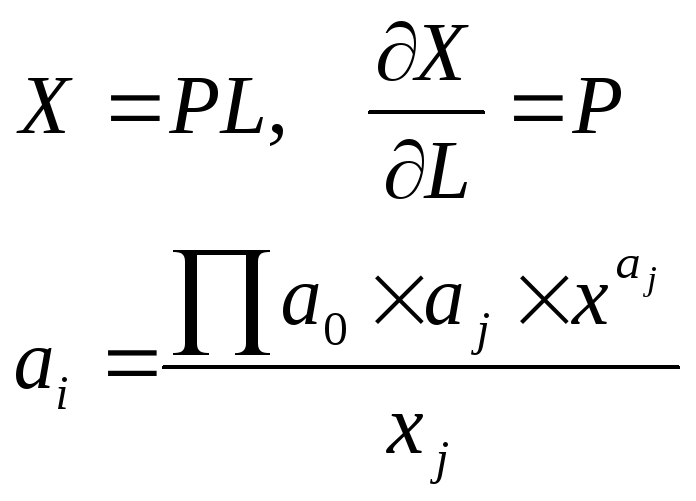
- так должно быть, иначе нет смысла

- то есть используемые ресурсы дают некоторую отдачу

С повышением потребления отдача снижается – закон убывающей отдачи, для которого

2. Отдача. Эластичность и взаимозаменяемость ресурсов.

Отдача от расширения масштаба производства характеризует поведение производственной функции в зависимости от пропорционального увеличения ресурсов.

n - ресурсов

Производственная функция характеризуется постоянной отдачей от масштаба производства

В общем случае отдача от расширения отдачи производства:

если n>1, то мы имеем дело с возрастающей отдачей от масштаба производства (эффект отдачи от масштаба производства);

если n=1 – постоянная отдача от масштабов производства;

если n<1 – убывающая отдача от расширения масштабов производства.

Локальные показатели измерения отдачи от расширения масштаба производства является показатель эластичности. Показатель эластичности выпуска продукции по отношению роста затрат j-го ресурса определяется:

- локальная эластичность по j-му ресурсу

если - коэффициент больше единицы.

Полная эластичность:

Рассмотрим эквивалентную взаимозаменяемость ресурсов:

При расчёте взаимозаменяемости ресурсов:

и тогда

Рассмотрим взаимозаменяемость двух ресурсов:

из этого следует, что предельная норма эквивалентной взаимозаменяемости ресурсов это есть: