Примеры и упражнения на базе среды matlab к разделу 1.
Ниже приводятся примеры, которые иллюстрируют основные теоретические положения, относящиеся к сфере математического моделирования цифровых систем. Каждый из примеров сопровождается листингом программного кода на языке MATLAB, реализующим необходимее построения. В ряде случаев даются необходимые комментарии.
Кроме того, здесь приводятся упражнения для самостоятельной работы. К некоторым из них прилагаются определенные рекомендации.
Пример
5_01. а) Необходимо сгенерировать
дискретный сигнал
в среде MATLAB, где
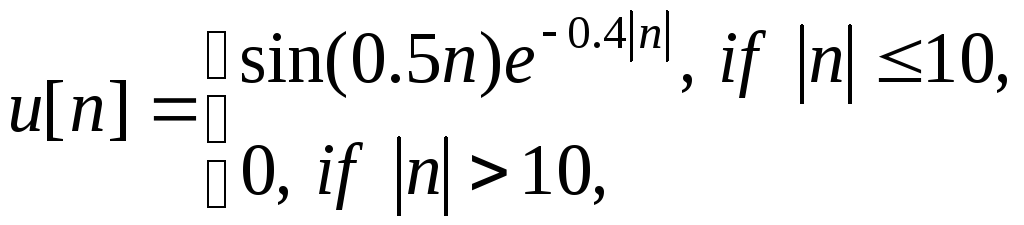
на сегменте
дискретного времени. Для построенной
конечной последовательности нужно
построить график решетчатой функции.
б)
Необходимо сгенерировать сдвинутый
ступенчатый единичный дискретный сигнал
на сегменте
,
где
,
и построить его графическое представление.
Пример выполняется с помощью программы, представленной в листинге 5.1. Обратим внимание на элегантный способ задания ступенчатого единичного сигнала. Результат работы программы по первому пункту показан на рис. 1.5.
Листинг 5.1
% Пример 5_01: Цифровые сигналы
clear;
% Базовые моменты времени
n1=-10:10;
% Заданные отсчеты сигнала
u1=sin(0.5*n1).*exp(-0.4*abs(n1));
u=[0 0 0 u1 0 0 0]; n=[-13 -12 -11 n1 11 12 13];
% График
figure(1); clf reset; h2=stem(n,u,'bo','fill');
set(h2,'LineWidth',2); grid on;
Xlabel('n'); ylabel('u[n]');
% Отсчеты единичного импульса
n1=-10; n2=10; n0=0;
nn=[n1:n2]; xx=[(nn-n0)>=0]; % !!!
% График
figure(2); clf reset;
h2=stem(nn,xx,'ro','fill');
set(h2,'LineWidth',2); grid on;
axis([-10,10,0,1.2]);
Xlabel('n'); ylabel('u[n]');
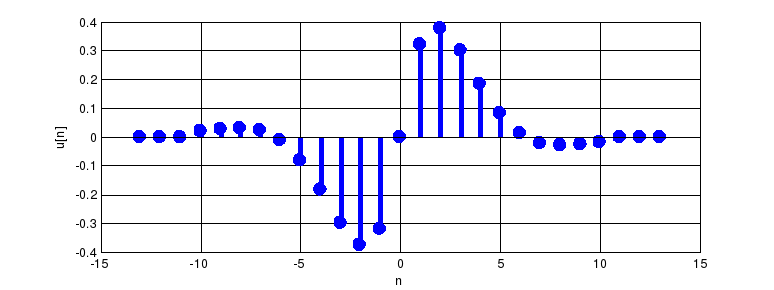
Рис. 1.5. График
функции
для примера 5_01.
Пример 5_02. Необходимо построить конечную импульсную характеристику DLTI-системы в виде последовательности
,
заданной в моменты
дискретного времени
.
Для применения формулы свертки нужно
сгенерировать две вспомогательные
последовательности: отраженную
последовательность
и сдвинутую последовательность
(
).
Все указанные последовательности должны быть представлены на отдельных графиках в едином окне функции plot среды MATLAB.
Данный пример можно выполнить с помощью программного кода на языке MATLAB, представленного в листинге 5.2.
Листинг 5.2
% Пример 5_02: Импульсная характеристика и свертка
clear;
% Моменты дискретного времени
n=-8:1:8;
% Импульсная характеристика
h=[0 0 0 0 0 0 0.1 0.2 0.4 0.5 0.6 0.8 0.7 0.5 0.2 0 0];
% Отражение от начала координат
h1=flipud(h'); h1=h1'; nn=length (h);
% Сдвиг вправо на 3 отсчета
h2=[0 0 0 h1(1:nn-3)];
% Графики последовательностей
figure(1); clf reset;
subplot(3,1,1); g1=stem(n,h,'bo','fill'); grid on;
set(g1,'LineWidth',2); axis([-8,8,0,0.9]);
title('1) impulse responce h(k)'); set(gca, 'XTickLabel',[]);
subplot(3,1,2); g2=stem(n,h1,'bo','fill'); grid on;
set(g2,'LineWidth',2); axis([-8,8,0,0.9]);
title('2) impulse responce h(-k)'); set(gca, 'XTickLabel',[]);
subplot(3,1,3); g3=stem(n,h2,'bo','fill'); grid on;
set(g3,'LineWidth',2); axis([-8,8,0,0.9]);
title('3) impulse responce h(-k+n), n=3');
Xlabel('k');
Результат работы приведенного фрагмента показан на рис. 1.3.
Пример
5_02. Необходимо построить реакцию
системы на входной сигнал
на отрезке времени
с отсчетами
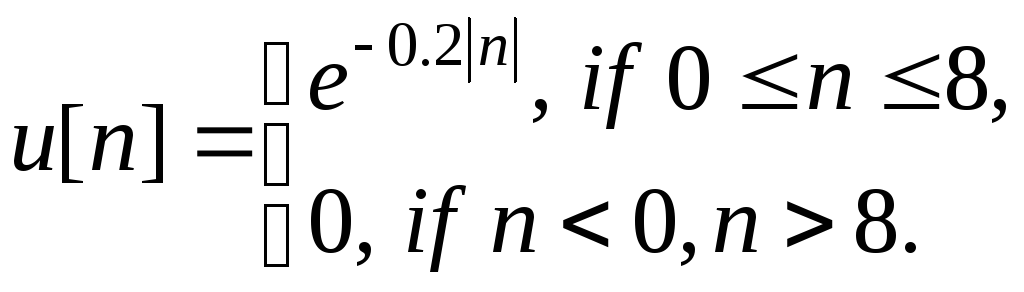
Построение
следует осуществить с помощью функции
conv
среды MATLAB для нахождения
свертки двух конечных последовательностей
и
.
При этом импульсная характеристика
задается конечной последовательностью
для моментов дискретного времени
.
Программный код для выполнения примера приведен в листинге 5.3.
Листинг 5.3
% Пример 5_03: Реакция на заданный входной сигнал
clear;
% Моменты дискретного времени
n=-5:22; nu=0:8; ni=0:9;
% Входной сигнал
u1=exp(-0.1*abs(nu));
u=[zeros(1,5) u1 zeros(1,14)];
% Импульсная характеристика
h1=[1 -1 2 3 -2 -1 -0.5 2 3 -1];
h=[zeros(1,5) h1 zeros(1,13)];
% Вычисление свертки
y1=conv(h1,u1);
y=[zeros(1,5) y1 zeros(1,5)];
% Графики последовательностей
figure(1); clf reset;
subplot(3,1,1); g1=stem(n,u,'bo','fill'); grid on;
set(g1,'LineWidth',2); axis([-5,22,0,1.2]);
title('1) input signal u[n]'); set(gca, 'XTickLabel',[]);
subplot(3,1,2); g2=stem(n,h,'bo','fill'); grid on;
set(g2,'LineWidth',2); axis([-5,22,-2.5,3.5]);;
title('2) impulse responce h[k]'); set(gca, 'XTickLabel',[]);
subplot(3,1,3); g3=stem(n,y(1:28),'bo','fill');
grid on;
set(g3,'LineWidth',2); axis([-5,22,-1,6]);
title('3) system responce y[n]');