36. Свойства производственной функции.

Производственная функция – функция, которая устанавливает количественную связь максимального объема выпуска продукции от производственных затрат.

1. ничего нельзя произвести если нет ресурсов:

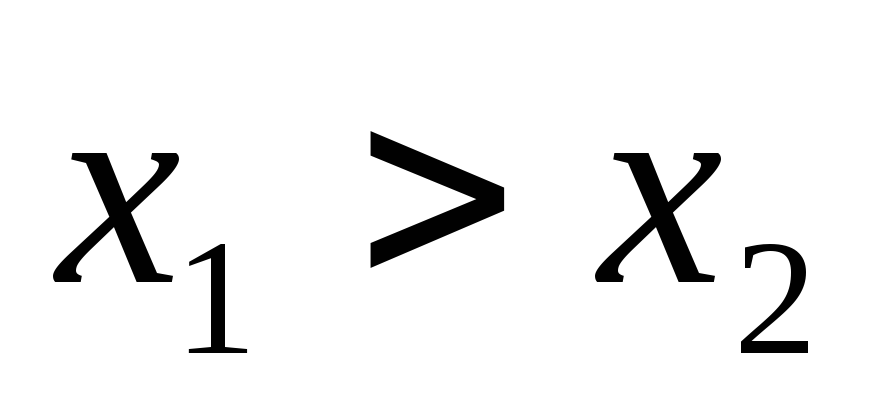2. Существует подмножество пространства затрат , называемые экономической областью, в которой увеличение любого вида затрат не сопровождается уменьшением выпуска продукции, т.е. если и - векторы затрат , то или , что значит, что чем больше затраты, тем больше производственные возможности, следовательно :

, где

- предельная производительность.

Для положительных производств будут рассматриваться положительные частные производные.

3. Существует выпуклое подмножество экономической области, в котором матрица Гэссе (матрица двух производных)

- отрицательно определена, т.е. вторая производная ,

Что говорит о том, что при увеличении затрат первого вида достигается такая область, в которой производительность падает.

4. Производственная функция характеризуется постоянной отдачей (доходом) от расширения масштаба производства, если выпуск продукции возростает в той же пропорции, что и затраты:

Производственная функция характеризуется возрастающей отдачей от расширения производства, если выпуск продукции возрастает в большей степени, чем затраты. В этом случае:

Производственная функция характеризуется убывающей отдачей от расширяемого масштаба производства, если выпуск продукции возрастает в меньшей степени, чем затраты.

Эластичность производства показывает изменение дохода при расширенном масштабе производства в заданной точке экономического производства:

37. Оптимизационная модель поведения фирмы

Допущение:

1. Производственная функция отражает только технологические условия производства (не учитывая внешнего воздействия)

2. Никаких внешних ограничений

3. На рынке совершенная конкуренция, при которой фирмы не могут влиять на цену реализации продукции, возможность свободного входа и выхода с рынка

38. Модель максимального выпуска продукции при заданных затратах

g=f(x)=f(x1…xn) и цены на факторы производства w=(w1…wn) и бюджет М на приобретение этих факторов производства.

Цель работы фирмы: f(x1…xn) -> max (x1…xn є С). (1)

(2)

Задача (1), (2) является задачей нелинейного программирования условной максимальной и может быть решена с использованием метода множителей Лагранжа или алгоритма Франка-Вульфа. Свойства оптимального решения:

1. В оптимальной точке х*=(х1*…хn*) при λ* выполняется условие:

Обозначает что предельные производительности факторов производства пропорциональные ценам на них.

2. Соотношение предельной производительности факторов производства = отношению их цен:

3. Предельная производительность факторов производства приходящаяся на одну денежную единицу в оптимальном плане в одинаковом для всех факторов производства:

39. Модель равновесия фирмы

Рассмотрим задачу максимизации прибыли фирмы при заданных ценах на продукцию р, на затраты производства w, и при заданном процессе производства. w=(w1…wn), f(x1…xn)=q. При этом критерии существования: П=Д-Z. П-прибыль, Д-доход. Доход=объем выпуска*на цену:Д=р*q. Z=w*q= Тогда П=р*f(x1…xn)- ->max - математическая модель равновесия фирмы.