3. Визначення стійкості укосу
У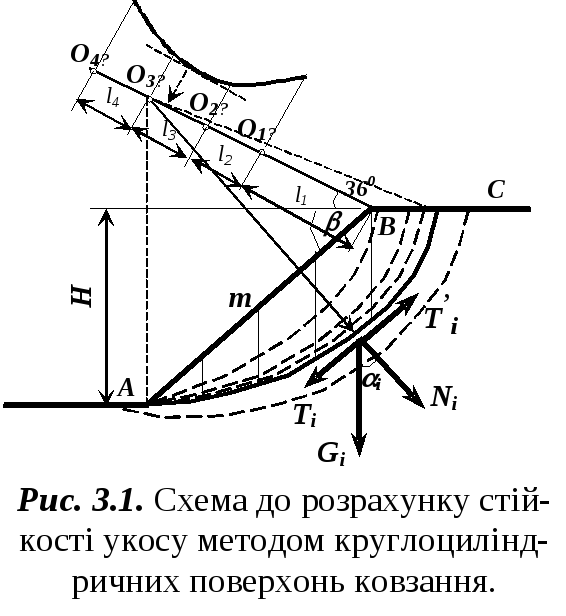
практиці визначення стійкості
укосу найчастіше
застосовують наближений метод
круглоциліндричних поверхонь ковзання.
Суть методу полягає в наступному:
в місцях мо-жливої
втрати стійкості грунту (рис 3.1)
прово-дять
круглоциліндричні поверхні, по яких
може відбуватися зсув, і визначають
відношення ут-римуючих
і зсуваючих
моментів сил.
Зрушуюча сила:
.
Утримуючі:
- сила, яка виникає за рахунок тертя;
- сила, яка виникає за рахунок зчеплення.
Тут
-
вага і-го
відсіку;
- кут нахилу поверхні ковзання
і-го відсіку до горизонту;
- довжина і-го відсіку.
Сума моментів зрушуючих сил
(3.1)
Сума моментів утримуючих сил
(3.2)
Розділивши
(3.1) на (3.2) і скоротивши
на
отримаємо коефіцієнт стійкості
укосу
(3.3)
Цю процедуру повторюють для інших
можливих поверхонь ковзання, для чо-го
міняють положення точки
.
Таким чином знаходять мінімальний
коефіцієнт стійкості
.
Розроблені методи, що дають змогу знайти
,
обмежуючись незначною кількістю
визначень
.
З верхньої точки укосу В проводять
похилу лі-нію під кутом
360 до горизонту
(рис. 3.1). На
цій лінії розміщують точки О1
О2 О3 О4
на відстанях
,
,
де
.
Ці точки прийма-ють за
центри обертання. Будують
сліди відповідних поверхонь ковзання,
для кож-ної з яких
розраховують значення коефіцієнта
стійкості за формулою (3.3).
Потім у відповідних точках відкладають
у деякому масштабі значення
у вигляді відрізків перпендикулярних
до лінії ВО. Через кінці цих
відрізків креслять плавну криву,
до якої проводять дотичну, паралельну
лінії ВО і точку дотику проектують
на цю ж лінію ВО. Для одержаної
п‘ятої точки О5
будують відповідну поверхню ковзання
і одержують мінімальне значення
коефіцієнта стійкості
.
Отримане значення
порівнюють з нормативним
,
де
- коефіцієнт надійності, який залежить
від класу капітальності будівлі і
приймається: 1,2
– для першого класу,
1,15
– для другого,
1,1
– для третього;
- коефіцієнт надійнос-ті,
який залежить від виду грунту
в основі і приймається для
пісків, окрім пилуватих 1,0;
для пісків пилуватих а також
пилувато-глинистих грунтів у
стабілізованому стані 0,9;
для пилувато-глинистих грунтів у
нестабілізованому стані 0,85;
для
скельних
грунтів: невивітрених
і слабовивітрених
1,0;
вивітрених
0,9;
сильновивітрених
0,85.
З практичного досвіду визначення стійкості методом круглоциліндричних поверхонь ковзання точку з найменшим коефіцієнтом стійкості можна знайти, провівши з нижньої точки укосу А вертикальний відрізок довжиною 2,5Н.
Приклад 3.1.
Визначити стійкість укосу методом
круглоциліндричних повер-хонь
ковзання. Висота укосу Н=6,0м,
довжина укосу Н=7,0м.
Характеристики грунту в укосі взяті
за результатами обчислень, виконаних
в задачах № 1 і № 2:
кН/м3
- для випадку, коли збільшення питомої
ваги погіршує умови роботи конструкції;
,
кПа
- для випадку, коли зменшення характеристик
погіршує умови роботи конструкцій.
Викреслюємо в масштабі схему укосу (рис. 3.2). Проводимо з нижньої точки укосу А вертикальний відрізок довжиною 2,5Н=2,5·6=15м. Подальші розрахунки ведемо в табличній формі (див. табл. 3.1).
Коефіцієнт стійкості укосу
Нормативний коефіцієнт стійкості
,
де
- для першого класу капітальності;
- в основі залягають пилувато-глинисті
грунти в стабілізованому стані.
О
скільки
,
то стійкість укосу забезпечена.
Таблиця 3.1
|
№ відсіку |
hi , м |
bi , м |
Вага відсіку, кН |
Δ hi м |
αi=arctgΔ hi/ bi град |
Ni =Gicos αi , кН |
Тi = Nitg φI , кН |
li = bi/cos αi , м |
Qi =cI li , кН |
Fi =Gisin αi , кН |
|
1 |
0,000 |
1,50 |
G1=0,5·1,211·1,5·19,21=17,45 |
0,075 |
2,86 |
17,43 |
7,75 |
1,502 |
25,08 |
0,87 |
|
1,211 |
||||||||||
|
2 |
1,211 |
1,50 |
G2=0,5(1,211+2,268)1,5·19,21=50,12 |
0,228 |
8,64 |
49,56 |
22,05 |
1,517 |
25,33 |
7,53 |
|
2,268 |
||||||||||
|
3 |
2,268 |
1,50 |
G2=0,5(2,268+3,166)1,5·19,21=78,29 |
0,388 |
14,50 |
75,80 |
33,73 |
1,549 |
25,87 |
19,60 |
|
3,166 |
||||||||||
|
4 |
3,166 |
1,50 |
G2=0,5(3,166+3,981)1,5·19,21=102,97 |
0,561 |
20,51 |
96,44 |
42,92 |
1,602 |
26,75 |
36,08 |
|
3,981 |
||||||||||
|
5 |
3,981 |
1,00 |
G2=0,5(3,981+4,266)1,0·19,21=79,21 |
0,481 |
25,69 |
71,38 |
31,77 |
1,110 |
18,54 |
34,34 |
|
4,266 |
||||||||||
|
6 |
4,266 |
1,50 |
G2=0,5(4,266+3,359)1,5·19,21=109,86 |
0,907 |
31,16 |
94,01 |
41,83 |
1,753 |
29,28 |
56,84 |
|
3,359 |
||||||||||
|
7 |
3,359 |
1,50 |
G2=0,5(3,359+2,181)1,5·19,21=79,82 |
1,179 |
38,17 |
62,75 |
27,93 |
1,908 |
31,86 |
49,33 |
|
2,181 |
||||||||||
|
8 |
2,181 |
2,00 |
G2=0,5·2,181·2,0·19,21=41,90 |
2,181 |
47,48 |
28,32 |
12,60 |
2,959 |
49,42 |
30,88 |
|
0,000 |
||||||||||
|
|
|
|
∑ |
6,000 |
|
|
220,63 |
|
232,13 |
235,47 |