рентген

11

Казанский государственный технический университет

им. А.Н.Туполева

Факультет физико-математической подготовки

Кафедра технической физики

КУРСОВАЯ РАБОТА

Рентгеноструктурный анализ. Определение постоянной

кристаллической решетки вещества.

по дисциплине

_____________Физика и диагностика поверхности__________________

_________________________________________________________________

Выполнил: ст. группы № _____________

________________________

Руководитель: __Манапов Р.А.___________

Оценка

<______ > { }

Принял: _____________ ( Манапов Р.А.)

“_____”___________2009 г.

г. Казань

Рентгеноструктурный анализ. Определение постоянной кристаллической решетки вещества.

1. Некоторые кристаллографические определения и обозначения.

В качестве схемы строения вещества принята пространственная решетка (ПР) или решетка Браве. ПР получаем, если исключим все особенности химической природы составляющих ее частиц - форму, размер и состав молекул, атомов или ионов и вместо частиц будем рассматривать точки (узлы решетки) - центры тяжести частиц. ПР характеризуется параллелепипидом повторяемости - элементарной ячейкой (ЭЯ). Параллельным переносом (трансляцией) ЭЯ в трехмерном пространстве строится ПР. Форма и размер ЭЯ характеризуются шестью константами: длинами ребер а, b, c и углами между ними  , , .

Рис.1. Пространственная кристаллическая решетка.

Для кубической решетки a= b= c и  = =  = 90⁰. Для построения такой решетки достаточно знать одну константу - a, называемую постоянной решетки. Постоянная решетки характеризует расстояние между идентичными атомами по осям координат. Существуют и более сложные решетки, в которых узлы расположены не только в вершинах ЭЯ. Такие решетки можно рассматривать как совокупность нескольких простых решеток, сдвинутых определенным образом одна относительно другой. Наиболее часто встречаются куб. решетки объемноцентрированные (ОЦК) и гранецентрированные (ГЦК). Решетку ОЦК можно представить как две простые, вложенные друг в друга так, что узлы одной находятся в центре ЭЯ другой. Решетку ГЦК - как 4 простые решетки, причем каждая вершина 2, 3 и 4 решеток находится в центре граней куба первой решетки. Следовательно, количество атомов, приходящихся на долю одной ЭЯ будет зависеть от типа решетки. Из рис. 2 видно, что в простой решетке на одну ЭЯ приходится один атом, так как любой узел в вершине принадлежит одновременно 8 соседним ячейкам (8 узлов х 1/8 атома = 1 атом). В ОЦК и ГЦК на одну ЭЯ приходится 2 и 4 атома.

Рис.2. Элементарные кубические ячейки: а - простая, b - ОЦК, с - ГЦК.

В ПР через отдельные группы атомов можно провести бесчисленное множество параллельных плоскостей. Совокупность параллельных атомных плоскостей называется семейством атомных плоскостей, а расстояние между ними - межплоскостным расстоянием - d. Число атомов входящих в ту или иную плоскость различно и тем меньше, чем меньше межплоскостное расстояние. Положение атомной плоскости в ПР определяется при помощи трех простых целых чисел (индексы Миллера). Они представляют собой величины, обратные отрезкам, отсекаемых плоскостью на осях координат. Индексы плоскости обозначаются буквами h, k, l и заключаются в круглые скобки (h, k, l). Нормаль к плоскости имеет те же индексы (индексы направлений), но заключенные в квадратные скобки [h, k, l]. На рис.3 показаны некоторые плоскости, принадлежащие различным семействам атомных плоскостей.

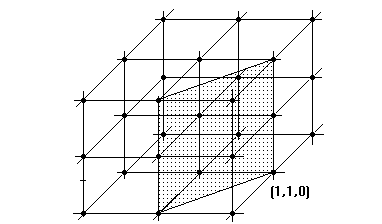
Рис. 3. Некоторые важные плоскости и их кристаллографические индексы.

Постоянная решетки, межплоскостные расстояния и индексы плоскости для кубической решетки связаны выражением:

.

2. Рентгеновское излучение.

Рентгеновское излучение возникает при бомбардировке какого -либо вещества электронами большой энергии. Для получения его используют специальные электровакуумные приборы - рентгеновские трубки, представляющие собой диод. Катод сделан из вольфрамовой проволоки в виде спирали. Спираль накаливается электрическим током и служит источником свободных электронов. Анод - массивный медный стержень, охлаждаемый водой и обращенный торцом к катоду. В торец анода впаивается пластинка какого-либо металла, называемого зеркалом анода. Под действием электрического поля, создаваемым приложенным к электродам трубки напряжением, свободные электроны с большой скоростью перемещаются к аноду и взаимодействуя с веществом зеркала анода резко тормозятся, в результате чего возникает рентгеновское излучение, состоящее из двух компонентов - тормозного и характеристического излучения. Тормозное излучение имеет непрерывный спектр вследствие того, что образование его происходит на разной глубине и к моменту торможения часть электронов теряет свою энергию вследствие потерь на ионизацию (в конечном счете - на тепло). Максимальную энергию имеют кванты, полученные при торможении электронов на самой поверхности зеркала анода:

eU = h = hc/ ,

где e- заряд электрона, U - напряжение на трубке,  - частота излучения, - длина волны, с - скорость света. Характеристическое излучение возникает при выбивании электронов из внутренних оболочек атомов зеркала анода и состоит из нескольких групп линий - серий, значительно отличающихся друг от друга по длине волны. Таких серий возможно 4 - K, L, M и N. Каждая серия состоит из определенного числа спектральных линий, которые обозначаются буквами греческого алфавита  , ,  c индексами 1, 2 и т.д. (например K_1 , K_2 , K_1 и т.д.) . Все линии спектра возникают одновременно, как только напряжение на трубке (а, следовательно, и кинетическая энергия электронов) достигает некоторого значения, называемого критическим потенциалом возбуждения данной серии - U_k. На рис. 4 схематически показано возникновение K- , L- и М-серий рентгеновского излучения:

Рис.4. Схема возникновения отдельных серий характеристического рентгеновского излучения.

Практическое значение в рентгеноструктурном анализе имеют лишь отдельные линии К- серии. При этом из соображений удобства проведения анализа, работу ведут на K_ -излучении, принимая, что _{ =} (_{1 +} _2)/2.

K_ -излучение поглощается селективным фильтром. В качестве фильтра берется вещество с порядковым номером в таблице Менделеева на единицу меньшим, чем порядковый номер вещества зеркала анода трубки (например, анод из Со - фильтр из Fe, анод из Cu - фильтр из Ni и т.д.). Приблизительное распределение энергии в рентгеновском спектре показано на рис. 5.

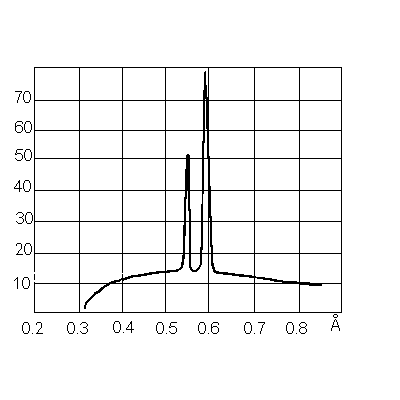
Рис. 5. Распределение интенсивности излучения рентгеновской трубки

3. Дифракция рентгеновских лучей.

Прохождение рентгеновских лучей через кристаллическое вещество сопровождается отклонением их от первоначального направления - дифракцией рентгеновского излучения. Сложную картину рассеивания рентгеновских лучей атомами допустимо рассматривать (Г.В.Вульф и отец и сын Брэгги) как отражение лучей от параллельных атомных плоскостей кристалла (рис. 6). Отражение в показанном на рис. 6 направлении будет происходить, если разность хода (отрезок ABC) лучей будет кратна длине волны, т.е. АВС = 2dsin = n где n - ряд целых чисел, т.е.

2dsin = n (Уравнение Вульфа-Брзгга).

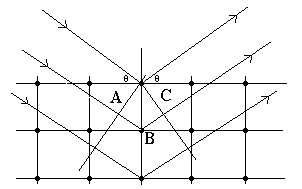
Рис. 6. К выводу уравнения Вульфа-Брэгга.

Каждое семейство атомных плоскостей будет давать ряд отражений, в зависимости от того, сколько целочисленных значений может принимать величина n, чтобы sin оставался меньше 1. Формула Вульфа-Брэгга позволяет:

1. Зная длину волны характеристических лучей и измерив углы скольжения можно вычислить межплоскостные расстояния - рентгеноструктурный анализ;

2. Зная межплоскостные расстояния и измерив углы скольжения можно вычислить длины волн отраженных рентгеновских лучей - рентгеноспектральный анализ.

4. Метод порошков (Дебая-Шеррера).

Поскольку кристаллические материалы в технике в основном поликристаллические, разработана методика исследования вещества в виде порошка или поликристалла. В силу беспорядочного расположения отдельных кристаллитов в таких веществах, всегда найдутся такие кристаллиты, у которых рассматриваемое семейство плоскостей будет удовлетворять условию Вульфа-Брэгга. Дифрагированные лучи будут образовывать семейство конусов, образованных дифракцией от соответствующих семейств атомных плоскостей с одинаковым межплоскостным расстоянием d. Регистрация отраженных лучей производится либо с помощью узкой фотопленки, уложенной по окружности, либо с помощью устройства для изменения угла скольжения (гониометр) и детектора рентгеновского излучения (сцинтилляционного или пропорционального счетчика). Оба метода имеют свои достоинства и недостатки, однако в силу легкости автоматизации измерений и обработки полученных дифрактограмм наиболее распространены приборы с регистрацией по второму способу - дифрактометры. Современные дифрактометры общего назначения (ДРОН) позволяют регистрировать дифрактограммы при:

1. Непрерывном автоматическом изменении угла дифракции (счетчик вращается с вдвое большей угловой скоростью) с записью интенсивности отраженных лучей;

2. Шаговом (с различным заданным интервалом) перемещении образца и детектора, при этом интенсивность регистрируется в течение заданного времени и результаты запоминаются.

Дифрактометрия используется при количественном фазовом анализе, прецизионном измерении периодов решетки, определении величины механических напряжений, при анализе формы и ширины интерференционного максимума, анализе текстур.

5. Обработка дифрактограмм и определение постоянной решетки.

По полученной дифрактограмме определяются межплоскостные расстояния, которые для кубического кристалла с постоянной решетки а связаны соотношением:

, для n=1, и

.

Объединяя эти два выражения, можно записать:

.

Отсюда следует, что для определения параметров решетки необходимо знать индексы плоскостей, участвующих в отражении рентгеновских лучей, т.е. проиндицировать рентгенограмму. Для каждой дифракционной линии, полученной при отражении от атомных плоскостей вещества, можно записать:

и т.д.

Или, исключая , имеем

Но индексы h, k, l - числа только целые, следовательно, и в правой части должно получиться отношение целых чисел. Вычислив sin² для всех линий, и разделив последовательно на sin²₁, получим ряд отношений:

В кубической решетке в зависимости от ее типа возможны три варианта отношений:

1. 1 : n : m : .... = 1 : 2 : 3 : ..., исключая числа 7, 15 и некоторые другие. Такой ряд отношений возможен при отражении от всех атомных плоскостей примитивной кубической решетки.

2. 1 : n : m : .... = 1 : 2 : 3 : ..., исключая числа 14, 30 и некоторые другие. Нетрудно заметить, что для чисел 7, 15 и некоторых других невозможно найти сумму квадратов трех простых чисел. Предположив, что решетка не простая, а объемноцентрированная, умножая числа ряда на 2, получаем новый ряд 2 : 4 : 6 : ... Умножение на 2 равносильно предположению о том, что первая дифракционная линия получена в результате отражения от второй атомной плоскости с индексом (0, 1, 1). Здесь уже любое число может быть представлено как сумма квадратов трех простых чисел.

3. 1 : n : m : .... = 1 : 1.33 : 2.66 : 3.66 : 4 : ... В этом ряду лишь некоторые числа являются целыми. Ищется множитель, который превращает полученное отношение в отношение целых чисел (например, используя множитель 3 получим 3 : 4 : 7 : 10 : ... Любое число в этих отношениях можно представить как сумму квадратов трех простых чисел, которые и будут искомыми индексами, например: 1 = 0² + 0² + 1² , 2 = 0² + 1² + 1² , 3 = 1² + 1² + 1² и т.д.

Определение параметра решетки.

Параметр или постоянную решетки вычисляют для каждой линии, затем берется среднее арифметическое. Значения а отличающиеся от средних величин больше чем на 0.03 А во внимание не принимаются.

Определение типа решетки.

В решетках разного типа отражения наблюдаются от различного сочетания атомных плоскостей. Существует следующее правило для определения типа решетки:

1. Если сумма индексов семейства плоскостей число четное, т.е. h + k + l = 2n, то решетка ОЦК.

2. Если индексы каждого семейства числа с одинаковой четностью, то решетка ГЦК.

3. Неподчинение первым двум правилам - примитивная решетка.

.

Практическая часть.

1. Построить дифрактограмму по полученным экспериментальным данным. Дифрактограммы получены с использованием излучения рентгеновской трубки с Fe-антикатодом (анодом). Для расчетов использовать длину волны К-излучения Fe: ₁ = 1.9399 А, ₂ = 1.9360 А, _ср/2 = 0.969 А.

2. Расшифровать дифрактограмму:

- определить углы 2 всех рефлексов,

- определить углы ,

- определить sin,

- определить межплоскостные расстояния d рефлексов,

- определить sin²,

- определить отношение sin²_i/ sin²₁ ,

- определить множитель, который преобразует отношения в ряд целых чисел,

- определить индексы h, k и l рефлексов,

- определить параметр ЭЯ как среднее значение по всем рефлексам и тип решетки Браве.

3. Определить вещество, сравнив вычисленные параметры с параметрами некоторых веществ, приводимых в таблице 2.

Исходные данные и результаты расчетов заносятся в таблицу, которая заполняется последовательно по столбцам.

№ п/п	Интен- сивность	2		sin	d	sin2	sin2n sin21	h, k, l	a
1
2
3
4
5

Вывод.

Таблица 2

Межплоскостные расстояния (d) и относительные интенсивности (I) линий некоторых поликристаллических веществ.

Ag		Al		Au
d	I	d	I	d	I
2.359 2.044 1.445 1.231 1.180 1.025	100 40 25 26 12 4	2.34 2.02 1.430 1.221 1.169 1.012 0.929	100 47 22 24 7 2 8	2.35 2.039 1.442 1.230 1.177 1.020	100 53 33 40 12 6
Co		Cu		Fe
d	I	d	I	d	I
2.04 1.77 1.253 1.066 1.021 0.886	100 44 22 22 5 3	2.09 1.81 1.278 1.090 1.044 0.904	100 46 20 17 5 3	2.01 1.428 1.166 1.010 0.904	100 15 38 10 8
Mo		Ni		Pb
d	I	d	I	d	I
2.225 1.574 1.285 1.113 0.995 0.908	100 21 39 11 17 7	2.03 1.76 1.246 1.062 1.017 0.881	100 42 21 20 7 4	2.86 2.48 1.75 1.493 1.429 1.238	100 50 31 32 9 2