Точкові оцінки

Статистичною оцінкою Ѳ* невідомого параметра Ѳ теоретичного розподілу називають функцію f( x_i,x₂, ... , x_n ) від спостерігаючих випадкових величин x_i, x₂, … , x_{n .}

Точковою називають статистичну оцінку, яка визначається одним числом Ѳ* =f(x₁, x₂, … , x_n)y, де x₁ ,x₂, … , x_n результати п спостережень над кількісною ознакою X (вибірка).

Незміщеною називають точкову оцінку, математичне сподівання якої дорівнює оцінюваному параметру, що оцінюється при будь-якому об’єму вибірки.

Зміщеною називають точкову оцінку, математичне очікування якої не дорівнює параметру що оцінюється.

Незміщеною оцінкою генеральною середньою (математичного очікування) є вибіркова середня

де x_і - варіанта вибірки, n_і –частота варіанта x_і, - об'єм вибірки. Зауваження 1. Якщо вихідні варіанти x_i – великі числа, то для спрощення розрахунку доцільно відняти від кожної варіанти одне і те ж число C, тобто перейти до умовних варіант u_i = x_i-C (у якості C вигідно прийняти число, близьке до вибіркової середньої; оскільки вибіркова середня невідома, число C вибирають «на око»). Тоді

= C + (Σn_iu_i)/n

Зміщеною оцінкою генеральної дисперсії служить вибіркова дисперсія

D_в = (n_i(x_i-)²)/n

ця оцінка є зміщеною, оскільки M[D_в] = (n-1/n)D_г

Більш зручна формула

D_в = ² – []² = (Σn_ix_i²)/n – [(Σn_ix_i)/n]²

Зауваження 2. Якщо вихідні варіанти x_i – великі числа, то доцільно відняти із всіх варіант одне і те ж число С, рівне вибірковій середньій або близьке до неї, тобто перейти до умовних варіантів u_i = x_i - C (дисперсія при цьому не зміниться).

Тоді

D_в(x) = D_в(u) = (Σn_iu_i²)/n – [(Σn_iu_i)/n]²

Зауваження 3. Якщо вихідні варіанти є десятковими дробами з k десятковими знаками після коми, то щоб уникнути дій з дробами, перемножують вихідні варіанти на стале число С=10^k, тобто переходять до умовних варіантів u_i=Cx_i. При цьому дисперсія збільшиться в С² разів. Тому, знайшовши дисперсію умовних варіант, треба розділити її на С²:

D_в(x) = D_в(u)/C²

Незміщеною оцінкою генеральної дисперсії служить виправлена вибіркова дисперсія

S²=n/(n-1)D_в=­Σn_i(x_i-)²/(n-1)

у умовних варіантах вона має вигляд

s_u² = (Σn_iu_i² – [Σn_iu_i]²/n)/(n-1)

причому якщо u_i = x_i – C, то s²x=s_u² ; якщо u_i = Cx_i , то s²x = s_u²/C²

Зауваження 4. При великому числі даних використовують метод

добутків або метод сум.

174. З генеральної сукупності добута вибірка об'єму n=50:

варіанту хi 2 5 7 10

частота пi 16 12 8 14

Знайти незміщену оцінку генеральної середньої.

175. З генеральної сукупності витягнута вибірка об'єму n=60:

хi 1 3 6 26

пi 8 40 10 2

Знайти незміщену оцінку генеральної середньої.

176. Знайти вибіркову середню по даному розподілу вибірки об'єму n=10:

хi 1250 1270 1280

пi 2 5 3

Розв’язання . Первинні варіанти — великі числа, тому перейдемо до умовних варіантів. ui= хi - 1270. У результаті отримаємо розподіл умовних варіант:

ui -20 0 10

пi 2 5 3

Знайдемо шукану вибіркову середню:

177. Знайти вибіркову середню по даному розподілу

вибірки об'єму n = 20:

хi 2560 2600 2620 2650 2700

пi 2 3 10 4 1

Вказівка. Перейти до умовних варіантів ui= пi -2620.

178. По вибірці об'єму n = 41 знайдена зміщена оцінка D_в = 3 генеральної дисперсії. Знайти незміщену оцінку дисперсії генеральної сукупності.

Розв’язання. Шукана незміщена оцінка рівна виправленій

дисперсії:

S² = D_в = = 3,075.

179. По вибірці об'єму n= 51 знайдена зміщена оцінка D_в = 5 генеральної дисперсії. Знайти незміщену оцінку дисперсії генеральної сукупності.

180. У результаті п'яти вимірювань довжини стрижня одним приладом (без систематичних помилок) отримані наступні результати (в мм): 92; 94; 103; 105; 106. Знайти: а) вибіркову середню довжину стрижня; б)вибіркову і виправлену дисперсії помилок приладу.

Розв’язання: а) Знайдемо вибіркову середню:

= 9 2 + ( 0 + 2 + 11 + 13 + 14)/5-=92+8 = 100.

б) Знайдемо вибіркову дисперсію:

D_в =x0 =[(92—100)²⁺ (94-~ 100)²+⁽103—100)²]/5+

+ [(105 —100)²⁺ (106—100)²]/5 = 34.

Знайдемо виправлену дисперсію:

181. У результаті чотирьох вимірювань деякої фізичної величини одним приладом (без систематичних помилок) отримані наступні результати: 8; 9; 11; 12. Знайти: а) вибіркову середню результатів вимірювань; би) вибіркову і виправлену дисперсії помилок приладу.

182. Знайти вибіркову дисперсію по даному розподілу

вибірки об'єму n=10:

хi 0,01 0,04 0,08

пi 5 3 2

Розв’язання. Для того, щоб уникнути дій з дробами

перейдемо до умовних варіантів ui= 100 хi . У результаті отримаємо розподіл

ui 1 4 8

пi 5 3 2

Знайдемо вибіркову дисперсію умовних варіант:

D_в (и) =

Підставивши в цю формулу умовні варіанти і їх частоти, отримаємо

D_в (и) = 7,21.

Знайдемо шукану вибіркову дисперсію первинних варіант:

D_в (X) = D_в(u)/1002 =7,21/10 000 = 0.0007.

183. Знайти вибіркову дисперсію по даному розподілу

вибірки об'єму n= 50:

xi 0,1 0,5 0,6 0,8

пi 5 15 20 10

Розв’язання. Перейти до умовних варіантів ui=10 хi

184. Знайти вибіркову дисперсію по даному розподілу

вибірки об'єму n = 50:

xi 18,4 18,9 19,3 19,6

пi 5 10 20 15

Рішення. Перейти до умовних варіантів ui=10 хi - 195

185. Знайти виправлену вибіркову дисперсію по даному розподілу вибірки n = 10:

xi 102 104 108

пi 2 3 5

Розв’язання. Перейдемо до умовних варіантів ui=хi - 104.

У результаті отримаємо розподіл

ui -2 0 4

пi 2 3 5

Знайдемо виправлену вибіркову дисперсію умовних варіант:

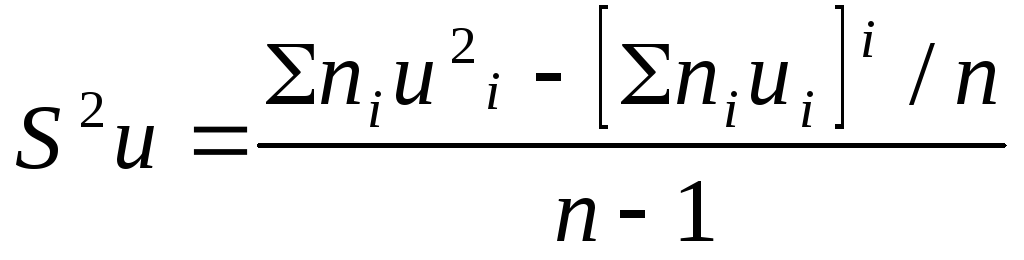
Підставивши в цю формулу умовні варіанти, їх частоти і об'єм

вибірки, отримаємо S²_u=6,93.

Всі первинні варіанти були зменшені на одне і те ж

постійне число З =104, тому дисперсія не змінилася, тобто

шукана дисперсія рівна дисперсії умовних варіант:

s²_x=s²_u=6,93.

186. Знайти виправлену вибіркову дисперсію по даному розподілу вибірки об'єму n = 100:

xi 1250 1275 1280 1300

пi 20 25 50 5

Розв’язання. Перейти до умовних варіантів ui=хi - 1275.

187. Знайти виправлену вибіркову дисперсію по

даному розподілу вибірки об'єму п=10:

xi 0,01 0,05 0,09

пi 2 3 5

Розв’язання. Для того, щоб уникнути дій з дробами, перейдемо

до умовних варіантів ui = lOO х_i . В підсумку отримаємо розподіл

ui 1 5 9

пi 2 3 5

Знайдемо виправлену вибіркову дисперсію умовних варіант

S²_x=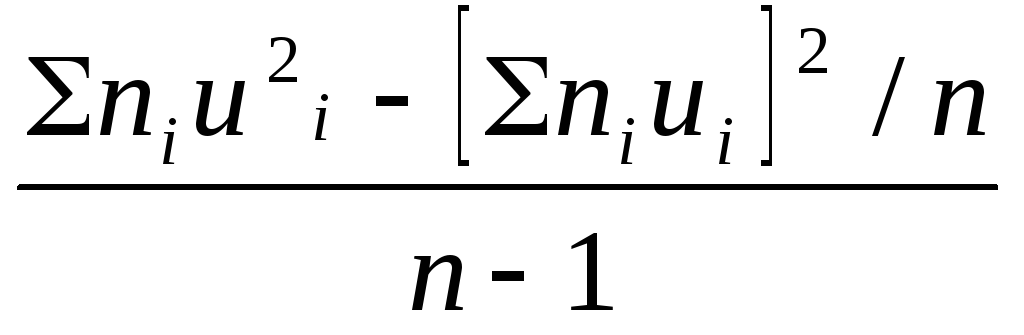

Підставивши в цю формулу дані задачі, отримаємо

S²_x =10,844.

Знайдемо шукану виправлену дисперсію первинних варіант:

S²_x = S²_x /1002 =10,844/10 000 ≈0,0085.

188. Знайти виправлену вибіркову дисперсію по даному розподілу вибірки об'єму n= 20:

xi 0,1 0,5 0,7 0,9

пi 6 12 1 1

Розв’язання. Перейти до умовних варіантів ui=10хi

189. Знайти виправлену вибіркову дисперсію по даному розподілу вибірки об'єму п = 10:

xi 23,5 26,1 28,2 30,4

пi 2 3 4 1

Розв’язання. Перейти до умовних варіантів ui=10хi -268.

190. З генеральної сукупності вибрана вибірка об'єму n = 60:

x_i 1 3 6 26

n_i 8 40 10 2

Знайти незміщену оцінку генеральної середньої.

191. Знайти вибіркову середню за даним розподілом вибірки об'єму n = 10:

x_i 1250 1270 1280

n_i 2 5 3

192. Нижче наведені результати вимірювання росту (у см) випадково відібраних 100 студентів.

Ріст 154-158 158-162 162-166 166-170 170-174 174-178 178-182

Число

Студентів 10 14 26 28 12 8 2

Знайти вибіркову середню і вибіркову дисперсію росту обстежених студентів. Вказівка. Знайти середини інтервалу і прийняти їх в якості

варіант.

193. Знайти вибіркову дисперсію за даним розподілом вибірки об'єму n =100:

x_i 340 360 375 380

n_i 20 50 18 12

Вказівка. Перейти до умовних варіант u_i = x_i – 360.

194. Знайти вибіркову дисперсію за даним розподілом вибірки об'єму n = 100:

x_i 2502 2804 2903 3028

n_i 8 30 60 2

Вказівка. Перейти до умовних варіант u_i = x_i – 2844.

195. Знайти виправлену вибіркову дисперсію за даним розподілом вибірки n = 10:

x_i 102 104 108

n_i 2 3 5

196. З генеральної сукупності добута вибірка об'єму п=12:

Варіанта

Частота

Оцінити з надійністю 0,95 математичне сподівання а нормально розподіленої ознаки генеральної сукупності за допомогою довірчого інтервалу.

197. За даними дев'яти незалежних рівноточних вимірювань деякої фізичної величини знайдені середнє арифметичне результатів вимірювань і «виправлене» середнє квадратичне відхилення s = 6. Оцінити дійсне значення вимірюваної величини за допомогою довірчого інтервалу з надійністю . Вважається, що результати вимірювань розподілені нормально.

Розв’язання. Дійсне значення вимірюваної величини дорівнює її математичному сподіванню а. Тому завдання зводиться до оцінки математичного сподівання (при невідомому а) за допомогою довірчого інтервалу

Всі величини, окрім t_y , відомі. За таблицею додатку 3 за

г = 0,99 і n = 9 знаходимо t_y = 2,36.

Підставивши = 30,1, t_y = 2,36, s = 6, n=9 в (*), отримаємо шуканий інтервал: 25,38 <α< 34,82.

198. За даними 16 незалежних рівноточних вимірювань деякої фізичної величини знайдені середнє арифметичне результатів вимірювань і «виправлене» середнє квадратичне відхилення s = 8. Оцінити дійсне значення вимірюваної величини з надійністю .

199. За даними вибірки об'єму n=16 з генеральної сукупності знайдено «виправлене» середнє квадратичне відхилення s= l нормально розподіленої кількісної ознаки. Знайти довірчий інтервал, що покриває генеральне середнє квадратичне відхилення про з надійністю 0,95.

Завдання зводиться до відшукання довірчого інтервалу

s(1 – q ) < σ < s(1+q) (якщо q<1) або 0 < σ < s (1+q) (якщо q>1) (*)

_{За заданим і n = 16 з таблиці додатку 4 знайдемо}

_{q=0,44. Оскільки, то, підставивши s = 1, в співвідношення (*), отримаємо шуканий довірчий інтервал 0,56 < σ < 1,44.}

_{200. За заданими вибірки об'єму п з генеральної сукупності нормально}

_{розподіленої кількісної ознаки знайдено «виправлене» середнє квадратичне відхилення s. Знайти довірчий інтервал, що покриває σ генеральне середнє квадратичне відхилення σ з надійністю 0,999, якщо: а) n =10, s = 5,1; б) n = 50, s=14.}

201. Проведено 12 вимірювань одним приладом (без систематичних помилок) деякої фізичної величини, причому «виправлене» середнє квадратичне відхилення s випадкових помилок вимірювань виявилося рівним 0,6. Знайти точність приладу з надійністю 0,99.Передбачається, що результати вимірювань розподілені нормально.

Розв’язання. Точність приладу характеризується середнім квадратичним відхиленням випадкових помилок вимірювань. Тому завдання зводиться до відшукання довірчого інтервалу, що покриває є із заданою надійністю .

Зо заданим і n = 12 з таблиці додатку 4 знайдемо

q=0,9. Підставивши s =0,6, q=0,9 в співвідношення (*), остаточно отримаємо

202. Проведено 10 вимірювань одним приладом (без систематичних помилок) деякої фізичної величини, причому «виправлене» середнє квадратичне відхилення s випадкових помилок вимірювань виявилося рівним 0,8. Знайти точність приладу з надійністю 0,95. Передбачається, що результати вимірювань розподілені нормально.