Теорема 2
Пусть
и
- квадратные матрицы
.
Тогда
.
Вычисление определителя с помощью разложения по строке (по столбцу)
Определение 24
Для квадратной
матрицы
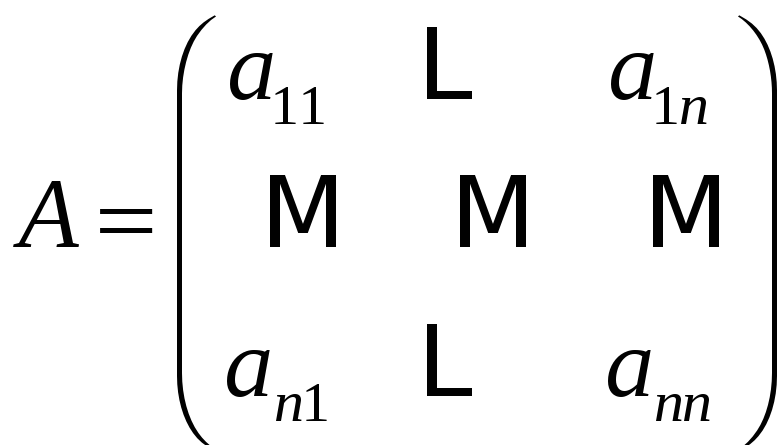минором
элемента
называется определитель матрицы,
получаемой из матрицы
вычеркиванием
-ой
строки и
-того
столбца.
Замечание
В определении
минора вычеркивается строка и столбец,
на пересечении которых стоит элемент
.
Определение 25
Алгебраическим
дополнением элемента
матрицы
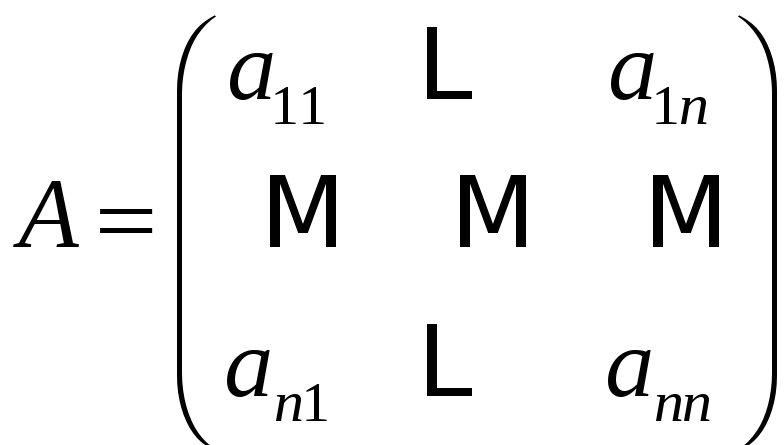называется число
.
Пример
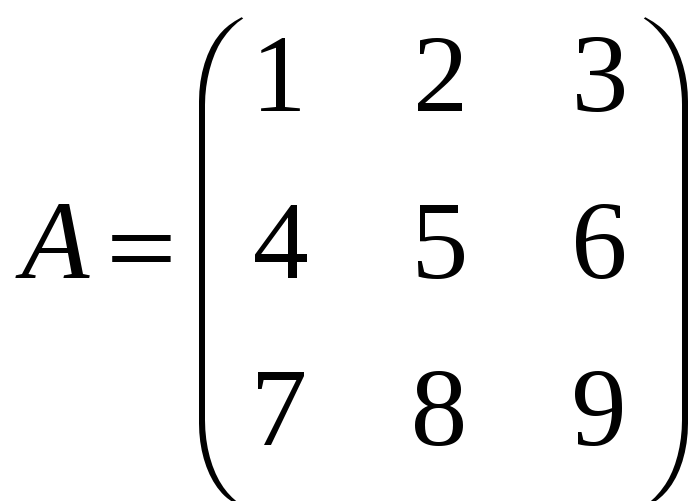
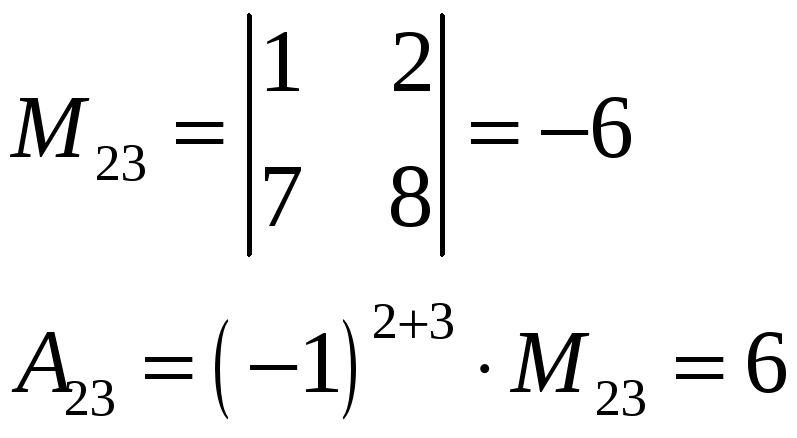
Лемма
Определитель
матрицы
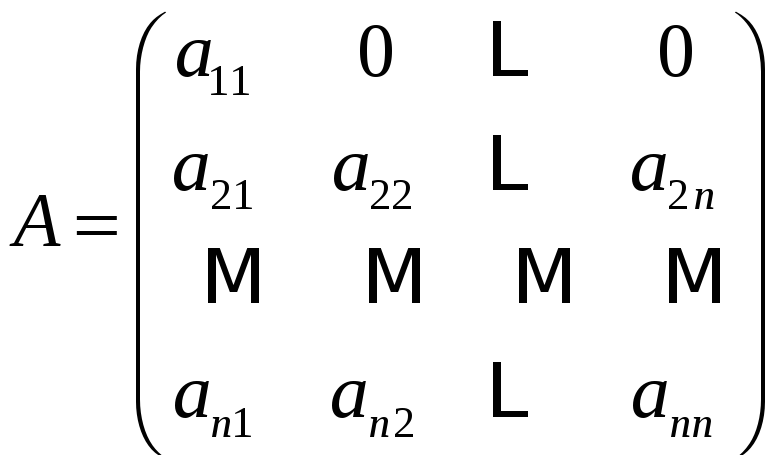равен
.
Доказательство
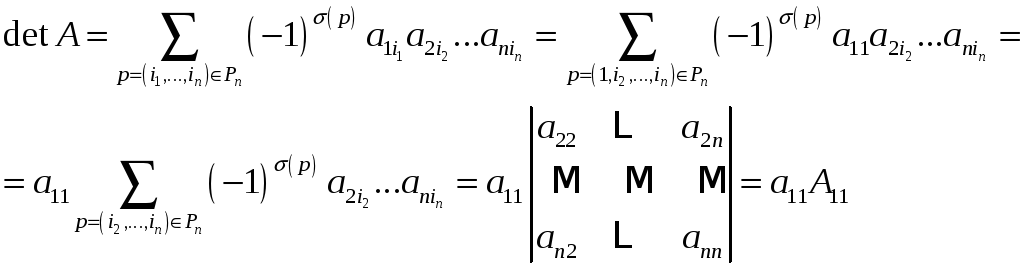
Лемма
Определитель
матрицы
,
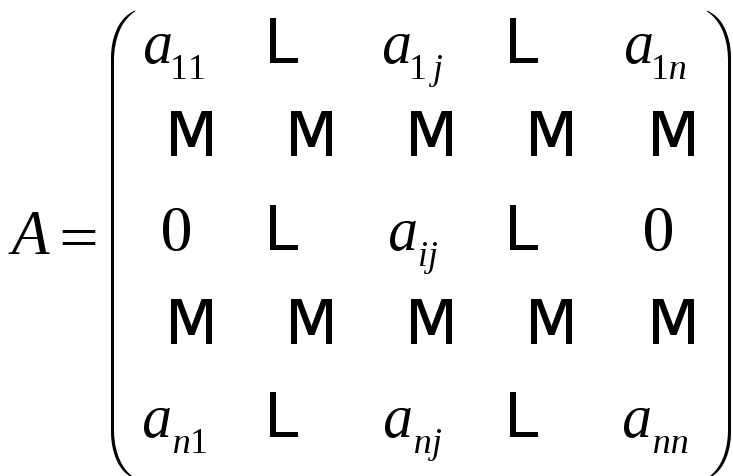в которой для фиксированного
,
при
,
равен
.
Доказательство
Переставим
последовательно строки
-ую
и
-ую,
затем
-ую
и
-ую
и т.д. Получим матрицу
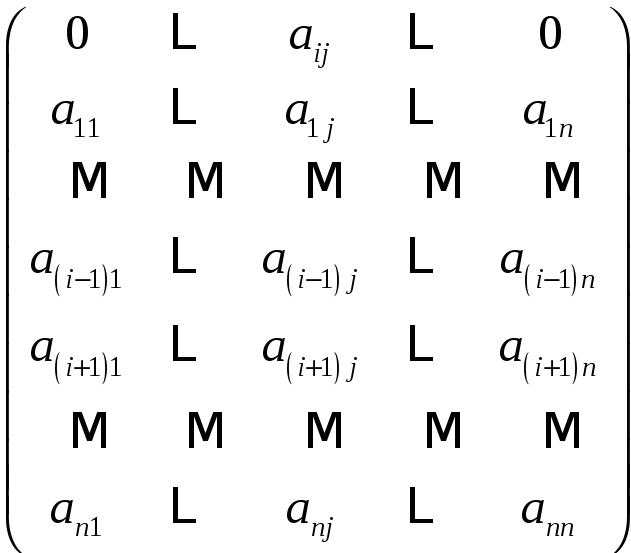
В полученной
матрице переставим последовательно
-ый
столбец с
-ым,
-ый
с
-ым.
Получим следующую матрицу:
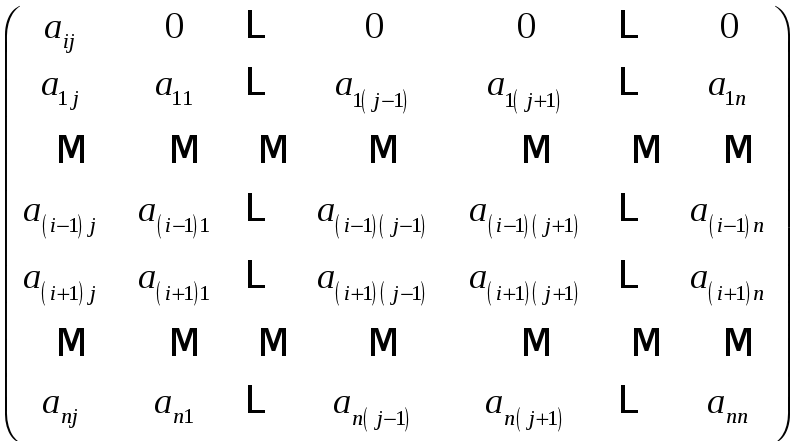
По предыдущей
лемме определитель этой матрицы равен
.
При перестановке строк и столбцов мы
сделали
перестановок, поэтому определитель
исходной матрицы равен
.
Теорема 3
Определитель
матрицы
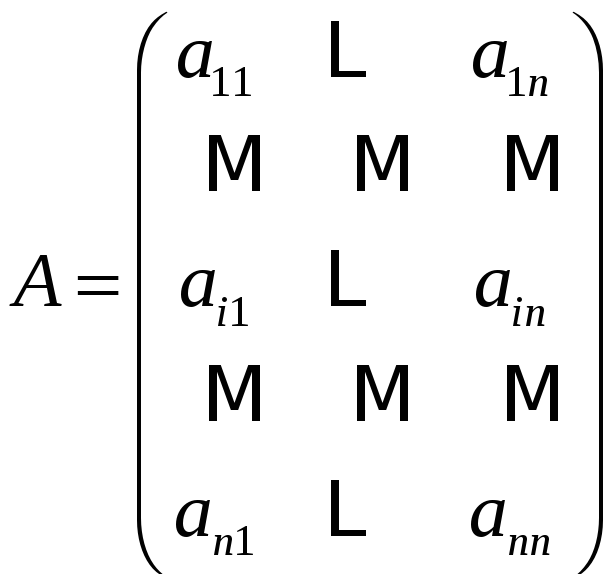может быть вычислен по формуле
.
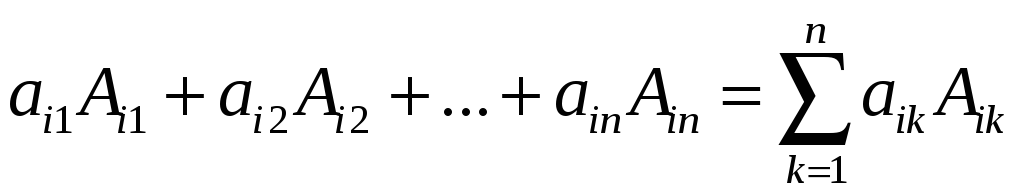Эта формула носит название разложения
по строке.
Доказательство
Строка
может быть представлена линейной
комбинацией строк
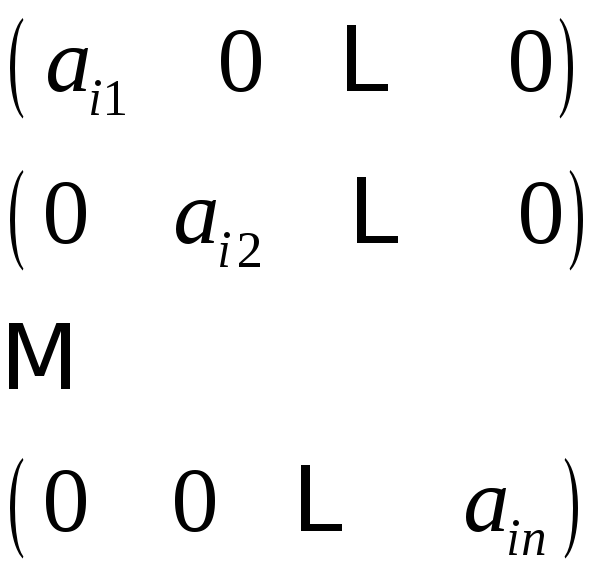
По следствию,
сделанному ранее и предыдущей лемме
получаем
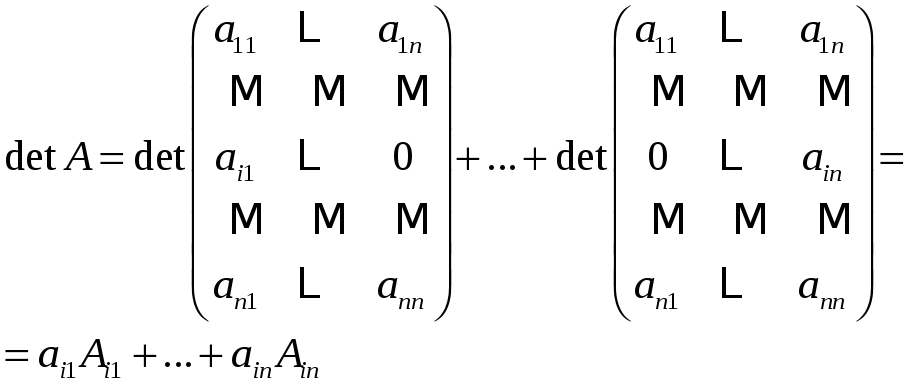
Теорема 4
Определитель
матрицы
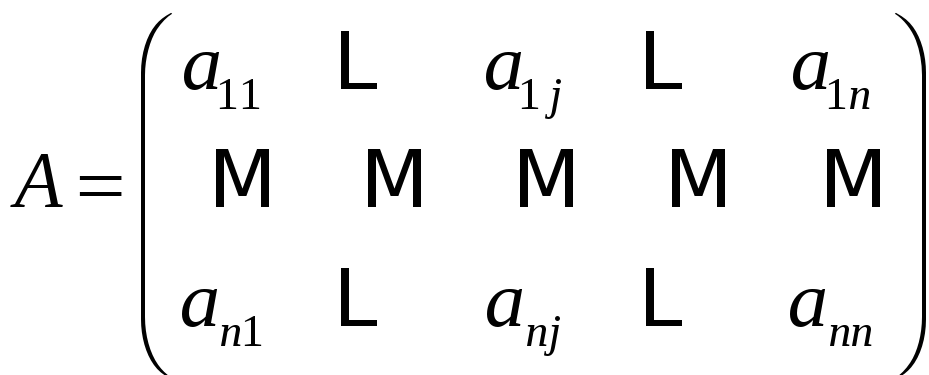может быть вычислен по формуле
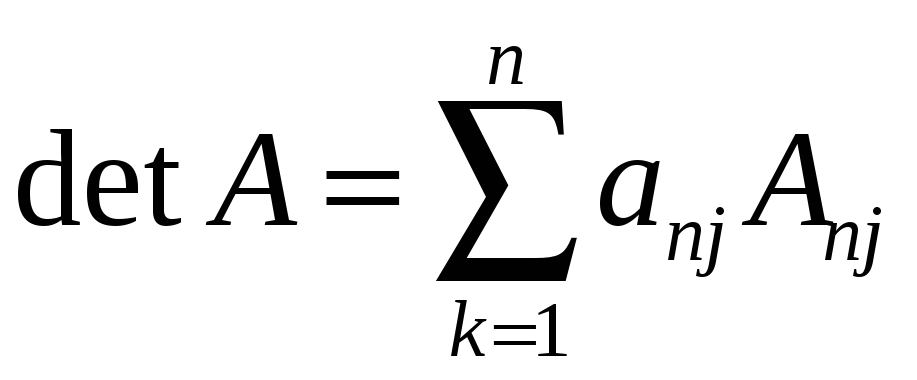(разложение по столбцу).
Пример
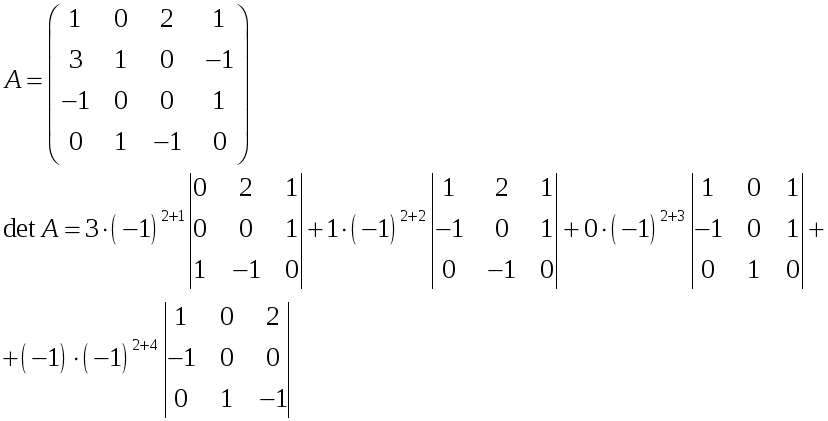Обратная матрица
Определение 26
Матрица
называется обратной к матрице
,
если
,
где
- единичная матрица.
Замечание
Матрицы
и
коммутируют. Матрицы
и
квадратные. Обратная матрица к матрице
обозначается
.
Свойства
Пусть матрицы
и
имеют обратные
и
.
Тогда
1)
2)
3)
Доказательство
1)
.
Значит матрица
является обратной к матрице
..
2)
3)
Значит
Теорема 5
Если матрица
имеет обратную, то обратная матрица
единственная.
Доказательство
Пусть
и
.
Тогда
.
Определение 27
Матрица, имеющая обратную матрицу называется обратимой.
Замечание
Существуют необратимые матрицы.
Теорема 6
Если матрица
- обратимая, то
.
Доказательство
Так как
обратима, то
такая, что
.
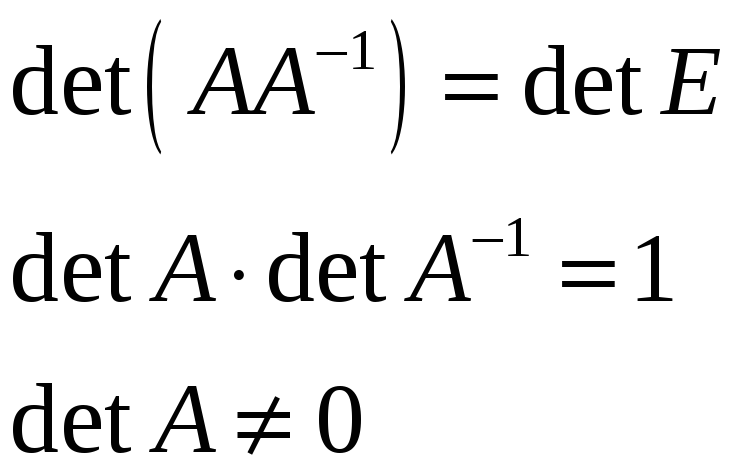
Лемма
Для квадратной
матрицы
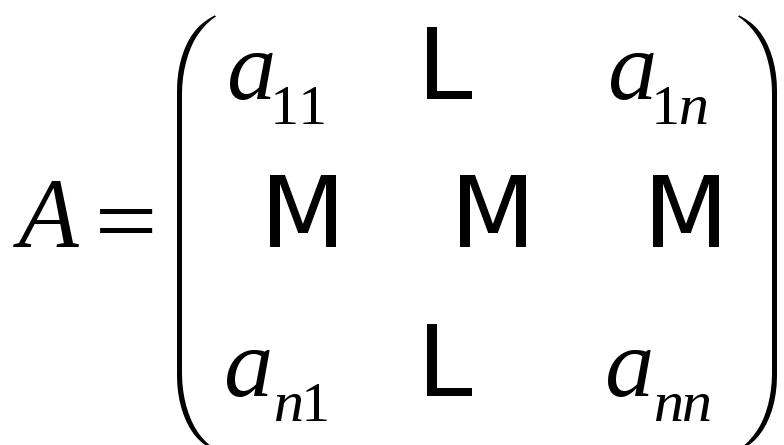выполняется
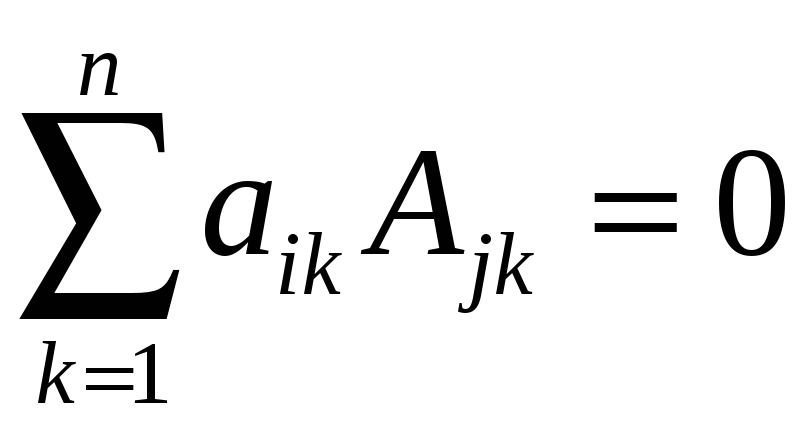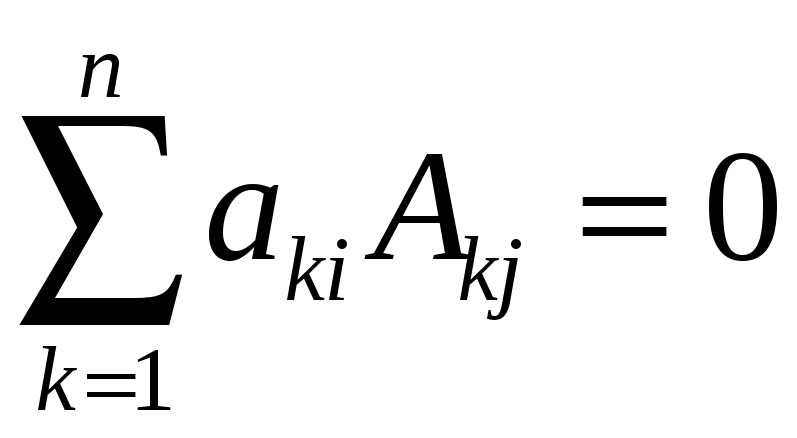при
при
.
Доказательство
Докажем, что
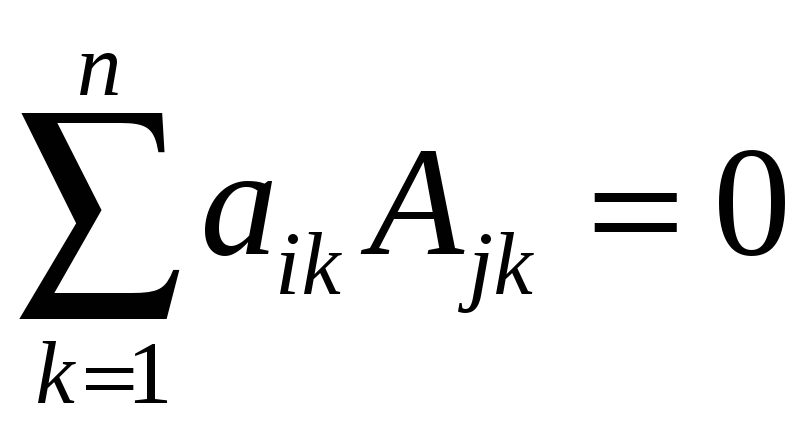при
.
Рассмотрим матрицу
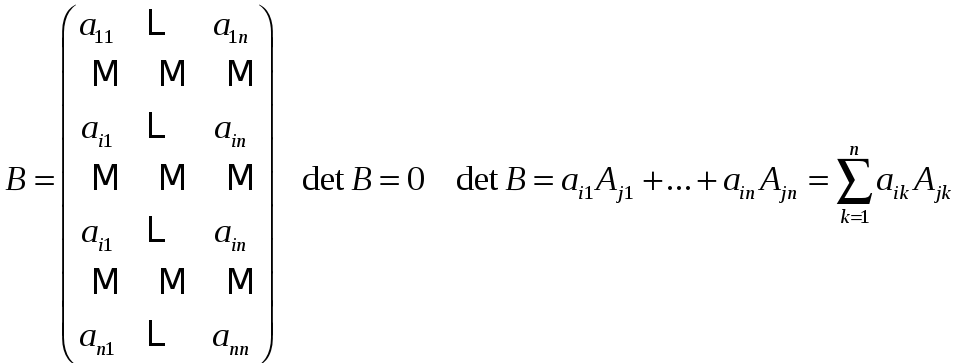
Теорема 7
Для матрицы
такой, что
обратная матрица может быть найдена по
формуле
,
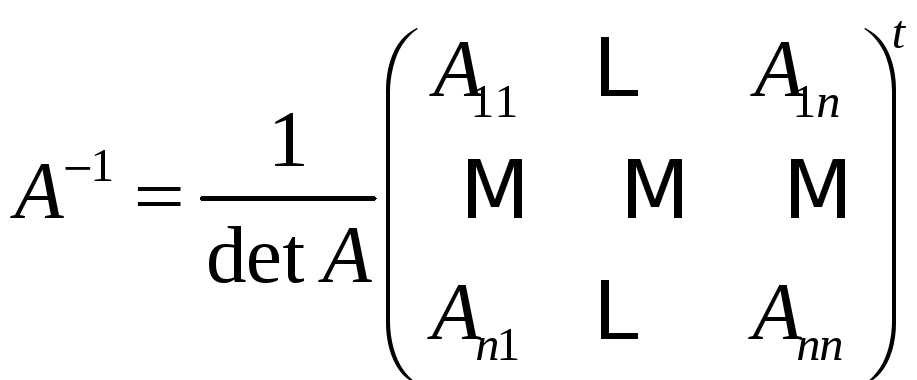где
- алгебраическое дополнение элемента
матрицы
.
Доказательство
Возьмем
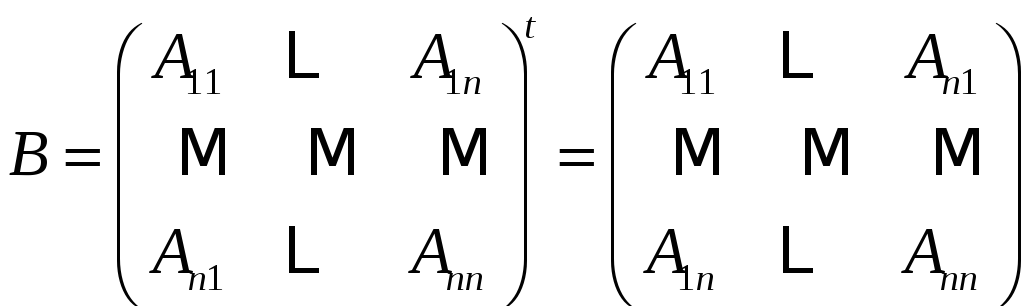
По лемме и теореме о разложении по строке
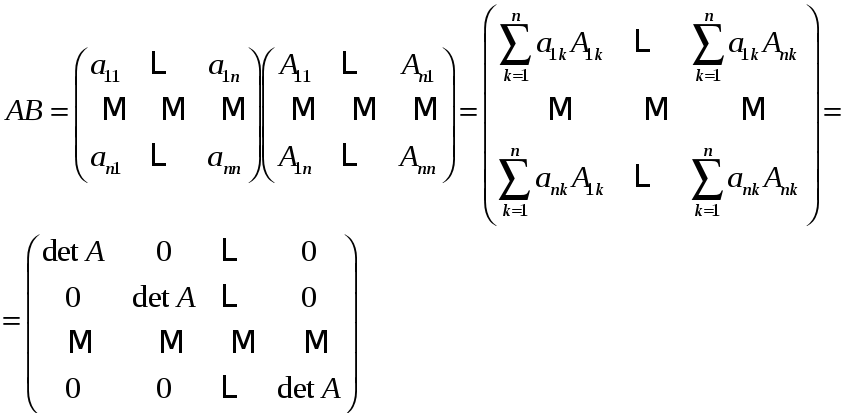
Поэтому
.
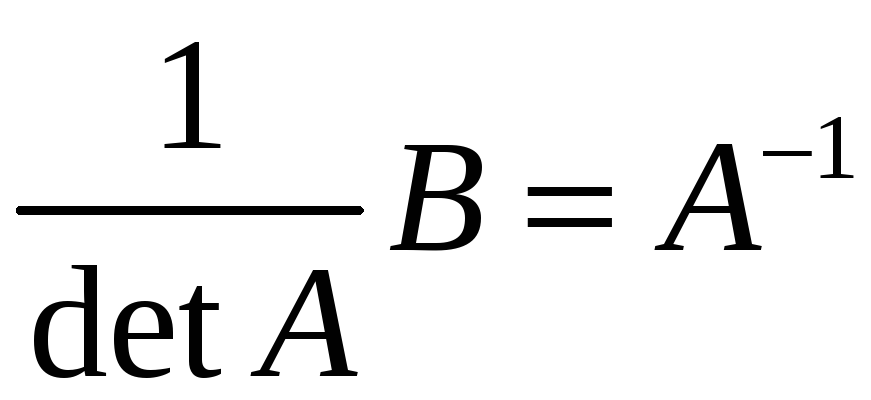Аналогично доказывается для
.