9. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.

Рассмотрим результат сложения двух гармонических колебаний одинаковой час­тоты , происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем

где  — разность фаз обоих колебаний, А и В — амплитуды складываемых колебаний. Уравнение траектории результирующего колебания находится исключением из выражений (145.1) параметра t. Записывая складываемые колебания в виде

и заменяя во втором уравнении cost на х/А и sint на , получим после несложных преобразований уравнение эллипса, оси которого ориентированы относите­льно координатных осей произвольно:

Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз .

Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Форма этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.

10. Затухающие колебания. Уравнение затухающих колебаний.

затухающие колебания — колебания, амплитуда которых из-за потерь энергии реальной колебательной системой с течением времени уменьшается.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

Решение уравнения рассмотрим в виде

где u=u(t). После нахождения первой и второй производных выражения и под­становки их получим

Решение уравнения зависит от знака коэффициента перед искомой вели­чиной. Рассмотрим случай, когда этот коэффициент положителен:

(если (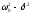)>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа ü+²и=0, решением которого является функция и=А₀cos(t+) (см. (140.1)). Таким образом, решение уравнения в случае малых затуханий ()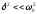

где

11. Дифференциальное уравнение затухающих колебаний осциллятора и его решение.

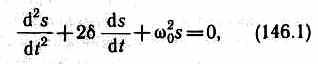
где s — колеблющаяся величина, описывающая тот или иной физический процесс, =const — коэффициент затухания, ₀ — циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

12. Циклическая (круговая) частота и период затухающих колебаний.

период затухающих колебаний

Циклическая (круговая) частота - это число полных колебаний в течении с:

. + амега в квадрате = амега нулевое в квад + бета в квад

13. Апериодический процесс.

Апериодический Процесс-переходный процесс в динамич. системе, при к-ром выходная величина, характеризующая переход системы от одного состояния к другому, либо монотонно стремится к установившемуся значению, либо имеет один экстремум (см. рис.). Теоретически может длиться бесконечно большое время. А. п. имеют место, напр., в системах автоматич. управления.

14. Закон изменения амплитуды затухающих колебаний.

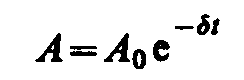— амплитуда затухающих колебаний,

а А₀ — начальная амплитуда. Промежуток времени =1/, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

15. Коэффициент затухания.

КОЭФФИЦИЕНТ ЗАТУХАНИЯ-количественная характеристика сопротивления колеблющейся системы колебательному движению.

16. Логарифмический декремент затухания и его связь с коэффициентом затухания.

Логарифмический декремент затухания - величина, показывающая скорость затухания собственных колебаний

логарифмическим декрементом затухания; N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. A(t) и А(t + Т) — амплитуды двух последовательных колебаний.

Логарифмический декремент затухания — по­стоянная для данной колебательной системы величина.

17. Изменение энергии осциллятора при затухающих колебаниях. Добротность осциллятора.

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

18. Вынужденные колебания. Уравнение вынужденных колебаний. Амплитуда и фаза вынужденных колебаний.

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

применяя впоследствии его решение для вынужденных колебаний конкретной физичес­кой природы (x₀ в случае механических колебаний равно F₀/m, в случае электромагнит­ных — U_m/L).

Решение уравнения равно сумме общего решения однородного урав­нения и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме . Заменим правую часть уравнения) на комплексную величину х₀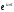

Частное решение этого уравнения будем искать в виде

Подставляя выражение для s и его производных в уравнение

получаем

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что =. Учитывая это, из уравнения (147.7) найдем величину s₀ и умножим ее числитель и знаменатель на

Это комплексное число удобно представить в экспоненциальной форме:

где

Следовательно, решение уравнения в комплексной форме примет вид

Его вещественная часть, являющаяся решением уравнения , равна

где А и  задаются, таким образом, частное решение неоднородного уравнения имеет вид

Решение уравнения равно сумме общего решения однородного уравнения

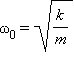– собственная круговая частота свободных колебаний, ω – циклическая частота вынуждающей силы.

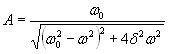-амплитуда