Зависимость анодного тока магнетрона от величины индукции магнитного поля
По мере увеличения В траектории будут искривляться все больше и при некотором “критическом” значении В=Вкр траектория электрона окажется касательной к поверхности анода (рис. Зв). При В>Вкр, кривизна траектории станет настолько значительной, что вылетев с катода, электрон будет описывать кривую, заканчивающуюся опять на катоде (рис. 3г). Его скорость в момент возвращения на катод уменьшится до нуля, после чего электрон начнет двигаться к аноду. Поскольку при этом ни один электрон не достигает анода, анодный ток Iа будет равен нулю.
Итак, при В<Вкр величина анодного тока не зависит от В, а при В >Вкр анодный ток вообще прекратится. При В= Вкр, происходит резкий спад (сброс) анодного тока до нуля (рис. Зв). Зная Вкр, можно найти отношение е/m.
Вывод рабочей формулы для расчёта удельного заряда электрона
Будем считать, что
В=Вкр
и, следовательно, траектория электрона
касательна к поверхности анода (рис.2).
Введём полярные координаты: радиус-вектор
r
(r=OC),
и угол поворота радиуса вектора
относительно вертикального направления
ОА.
Вектор скорости
электрона
можно разложить
на составляющую, направленную
перпендикулярно к радиусу, и составляющую
,
направленную вдоль радиуса. Считаем,
что при вылете из катода при r=О,
.
При r=b траектория электрона касательна к аноду. Следовательно, Vrb=О, Vφb=Vb
для точки касания при r=b можно записать на основании формулы:
,
(3) где
Ua-
разность потенциалов между анодом и
катодом
Отсюда, находим:
(4)
Для определения е/m
этого уравнения не достаточно, т.к.
неизвестна величина
.
Согласно второму закону динамики для
вращательного движения имеем:
(5)
Момент количества движения электрона в любой момент времени равен:
(6)
Сила Fе момент не создаёт, т.к. линия её действия проходит через точку О. Поэтому момент силы, действующей на электрон, задаётся только силой Fл (рис.2).
Так как, в нашем случае: Fл=еVВкр (см. формулу (2), тогда:
(7)
Из рис.3 видно, что
,
поэтому:
(8)
Произведение
можно
записать так:
(9)
тогда из уравнения (5) с учётом (6) и (9) получим:
(10)
Это выражение представляет равенство производных двух функций. Т.к. функции, производные которых равны, могут отличаться лишь аддитивной постоянной, можно записать:
mVφr
=
еВкр
r2+С
(11)
Постоянная С может быть определена из начальных условий. При r=0, Vφ=0.
Тогда
еВкра2+С=0,
откуда:
С=-
еВкра2,
Подставляя значение С в (11), найдём зависимость Vφ от радиуса для любой точки траектории:
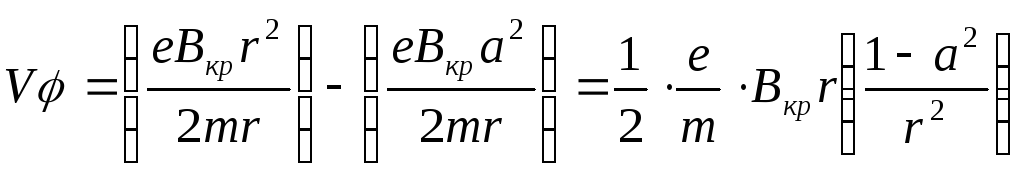(12)
При
:
(13)
Возводя Vφb в квадрат и подставляя в (4), получим:
(14)
Из этого квадратного уравнения можно найти е/m. Так как решение е/m=0 нас не интересует, находим:
(15)