§27. Закон сохранения заряда.

Запишем уравнение Максвелла: . Подействуем на него оператором скалярно. Получаем:

Но дивергенция всякого ротора равна нулю, поэтому в результате получаем:

- уравнение непрерывности

Проинтегрируем обе части этого уравнения по некоторому объёму:

, где -единичный вектор нормали

определяет количество заряда выносимого через поверхность объёма. Если - острый, то заряд выносится из объёма и -положителен. Если тупой, то заряд приходит в объём и - имеет знак минус.

§28. Типы калибровок. Уравнения Даламбера для потенциалов

Перепишем уравнения Максвелла:

1.Калибровка Лоренца

Тогда уравнение первое уравнение Максвелла перепишется в следующем виде:

□- оператор Даламбера

□- уравнение Даламбера

Это уравнение есть – неоднородное дифференциальное уравнение в частных производных.

□- оператор гиперболического типа.

Для 4-го уравнения Максвелла имеем:

□

Все, имеющие физический смысл, результаты должны быть градиентно-инвариантыми:

В силу калибровки Лоренца получаем:

□

Т.е. функция должна удовлетворять однородному уравнению Даламбера (его ещё называют волновым уравнением)

2.Калибровка Кулона

- калибровка Кулона

Уравнение (А) перепишется в следующем виде:

- уравнение Пуассона.

Если же (в пустоте), то уравнение Пуассона принимает вид:

-уравнение Лапласа.

получаем, что функция должна удовлетворять уравнению:

3.Калибровка поперечных волн

Полагаем есть функция только координат.

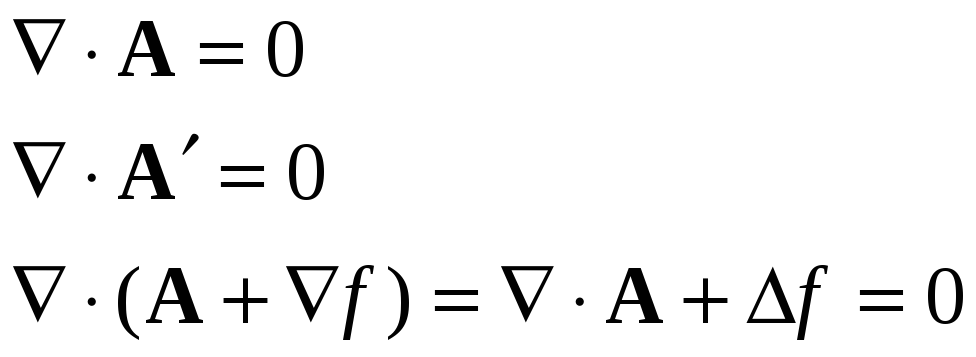
Значит функция должна удовлетворять уравнению:

- здесь k – волновой вектор

§29. Уравнения Максвелла в среде без учёта пространственно-временной дисперсии. Переход от микро к макро

С помощью этих уравнений можно описывать электромагнитное поле в среде. В среде будем ставить индекс «»=микро

включает в себя как связанные, так и свободные заряды в веществе. Каждой точке пространства ставится в соответствие функция . Это значит, что мы заменяем реальную среду моделью – сплошной средой, т.е. мы свойства разных точек «размазываем» по пространству. Существуют следующие способы описания сплошной среды на основе реальной среды:

1. Усреднение по некоторому физическому объёму и времени .

2. Статистическое усреднение. Считаем что у нас есть макроскопически-идентичный ансамбль систем(т.е. все внешние условия одинаковы). Здесь производятся измерения для отдельных ансамблей, а потом происходит усреднение. Этот способ более предпочтителен.

Усреднение будем обозначать символами «< >». Отметим, что усреднение коммутативно с дифференциальными операторами.

Итак, усредняем:

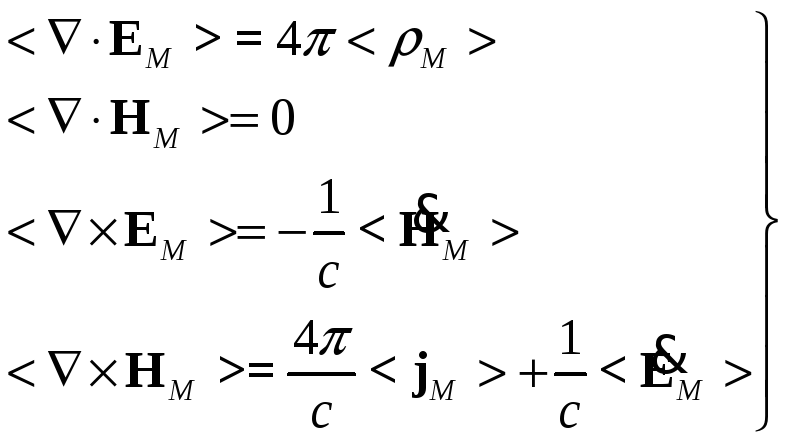
Среда под действием внешнего электромагнитного поля поляризуется, т.е. реагирует на внешнее воздействие. В случае, когда отсутствует пространственная дисперсия, поляризация характеризуется векторами электрической и магнитной поляризации . Можно показать, что и выражаются через :

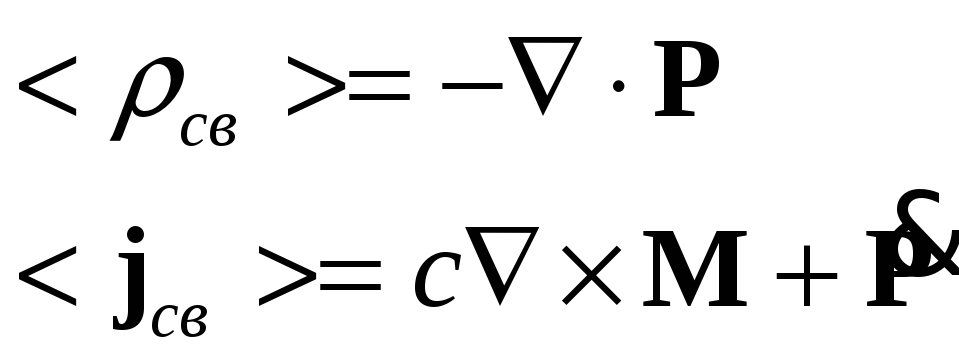
Введём обозначения: ;

Перенесём второе слагаемое из правой части в левую и объединим его с :

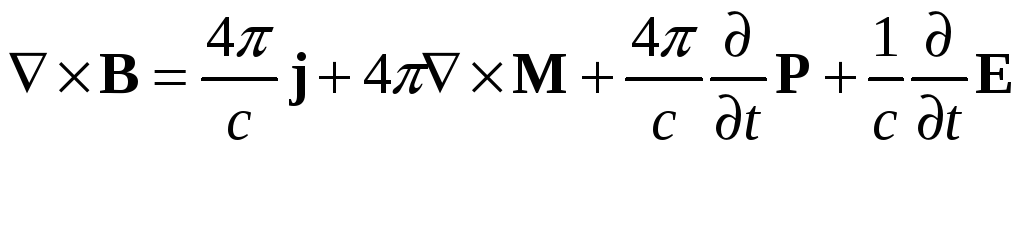
Итак, уравнения Максвелла для среды имеют вид: