Задачи по курсу «Теоретическая механика и теория поля» и их решение.

[ 1.] Наити функцию Лагранжа двойного плоского маятника , находящегося в однородном поле тяжести (ускорение силы тяжести g).

Решение. в качестве координат берём углы φ₁ и φ₂, которые нити l₁ и l₂ образуют с вертикалью. Тогда для точки m₁ имеем:

чтобы найти кинетическую энергию второй точки, выражаем её декартовы координаты x₂, y₂ (начало координат в точке подвеса, ось y – по вертикали вниз) через углы φ₁ и φ₂:

после этого получим:

окончательно:

2 . Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m₂, точка которого (с массой m₁ в ней) может совершать движения по горизонтальной прямой.

Решение. Вводя координату x точки m₁ и угол φ между нитью маятника и вертикалью, получим:

[3.] Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

Решение. В декартовых координатах x, y, z:

В цилиндрических координатах r, φ, z:

В сферических координатах r, θ, φ:

[4.] Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса материальной частицы.

Ответ: =-p_z

=0, =-p_y

5. Определить скобки Пуассона, составленные из компонент М.

Ответ: =-M_z, =-M_x , =-M_y.

6*. Показать, что

=0, ,

где φ – любая скалярная функция координат и импульса частицы.

Указание. Скалярная функция может зависеть от компонент векторов r и p только в комбинациях r²,p², . Поэтому

и аналогично для .

7*. Показать, что

=,

где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.

Указание. Произвольный вектор f(r, p) может быть написан в виде где - скалярные функции

8. Выразить амплитуду и начальную фазу колебаний через начальные значения x₀, v₀ координаты и скорости.

Ответ: ,

9 . Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.

Решение. Потенциальная энергия пружины (с точностью до малых величин высшего порядка) равна произведению силы F на удлинение δl пружины. при x<<l имеем:

,

так что U=Fx²/2l. Поскольку кинетическая энергия есть то

10. Найти частоту колебаний маятника, точка подвеса которого (с массой m₁ в ней) способна совершать движение в горизонтальном направлении.

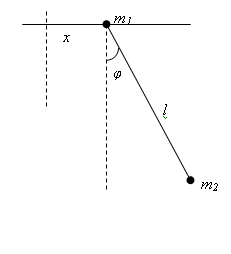
Решение. При φ<<1 находим:

Отсюда

.

1 1. Определить малые колебания двойного плоского маятника.

Решение. Для малых колебаний найденная в задаче 1 параграфа 5 функция Лагранжа принимает вид :

.

Уравнения движения:

После подстановки (23,6) :

Корни характеристического уравнения:

Ответ: .

При частоты стремятся к пределам и , соответствуют независимым колебаниям двух маятников.

12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

Решение.

13. Вычислить где p – постоянный вектор.

Решение.

14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы:

если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.

Решение. Умножим искомый интеграл на постоянный вектор р:

Так как вектор р произволен, то

.

Аналогично показывается, что

15. В равномерно заряженном шаре с объемной плотностью заряда имеется шарообразная полость, центр которой расположен на расстоянии а от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и .

Решение. Из принципа суперпозиции полей следует, что искомая напряженность поля равна разности напряженности электрического поля, создаваемого шаром без полости, и напряженности поля зарядов, заполняющих при этом полость.

Поле внутри полости

поле внутри шара (но вне полости)

поле снаружи шара

где - радиус-вектор, проведенный из центра шара к центру полости.

[16.]Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара. Объёмная плотность заряда равна , радиус шара R.

Решение.

при

при

17. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

Решение. Потенциал точечного заряда является решением уравнения

. (1)

Представим и в виде разложений в интеграл Фурье:

(2)

Подставляя соотношения (2) в уравнение (1) и приравнивая в подынтегральных выражениях коэффициенты при , получим

.

18. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону:

Решение. .

19. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

Решение. Предположив, что заряд расположен в начале координат, решим уравнения

Направим оси декартовой системы координат по главным осям тензора диэлектрической проницаемости. Тогда

Подставим соотношения (2) в уравнение (1):

Заменой уравнение приводится к виду

Здесь использовано свойство δ-функции:

Решение уравнения (4) имеет вид

где

20. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью j. Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

Решение. H=1/2

Экзаменационные вопросы по курсу «Теоретическая механика и теория поля».

[1.] Обобщенные координаты.

2. Описание эволюции системы в конфигурационном пространстве.

[3.] Принцип наименьшего действия в классической механике.

[4.] Уравнения движения Лагранжа.

5.Функция Лагранжа и ее свойства.

[6.]Функция Лагранжа простейших систем.

7. Интегралы движения (метод Лагранжа).

8. Свойства симметрии пространства и времени.

[9.] Законы сохранения.

10. Задача двух тел и сведение ее к эквивалентной одномерной.

11. Особенности движения частицы в центральном поле.

12. График эквивалентного одномерного потенциала.

[13.] Обобщенный импульс.

14. Функция Гамильтона и ее свойства.

15. Функции Гамильтона простейших систем.

[16.] Интегралы движения (метод Гамильтона).

[17.] Скобки Пуассона и их свойства.

18. Канонически сопряженные величины.

19. Описание эволюции системы в фазовом пространстве.

20. Малые колебания.

21. Свойства потенциальной энергии.

22. Колебания системы с одной степенью свободы.

[23.] Характеристическое уравнение.

24. Колебания системы с n-степенями свободы.

25.Дисперсионное уравнение.

[26.] Нормальные координаты.

27. Преобразование Лежандра и уравнения движения Гамильтона.

28. Динамические переменные в методах Лагранжа и Гамильтона.

[29.] Уравнения Максвелла для электромагнитного поля в вакууме.

[30.]Потенциалы электромагнитного поля в вакууме.

[31.]Градиентная инвариантность.

32. Закон сохранения заряда.

33. Объемная плотность точечного заряда.

34. Типы калибровок: Лоренца, Кулона, поперечных волн.

35.Уравнения Даламбера для потенциалов электромагнитного поля в вакууме.

36. Уравнения Максвелла для электромагнитного поля в среде без пространственно-временной дисперсии.

37. Потенциалы электромагнитного поля в среде.

38. Функциональные соотношения D=D(E), B=B(H), j=j(E) без учета пространственно-временной дисперсии.

39. Нелинейные, неоднородные и анизотропные среды.

40. Уравнения Максвелла для стационарного электромагнитного поля в среде.

41. Функция Грина уравнения Пуассона.

42. Некоторые задачи электростатики.

43. Некоторые задачи магнитостатики.

44. Приближение линейного тока.

[45.]Уравнения Максвелла для квазистационарного электромагнитного поля .

[46.]Условие квазистационарности поля и глубина его проникновения.

[47.] Уравнения Максвелла для электромагнитных волн в вакууме.

[48.] Волновое уравнение.

49. Решение волнового уравнения в случае плоской волны.

[50.]Плоская монохроматическая волна.

Экзаменационные вопросы по курсу «Теоретическая механика и теория поля».(план минимум)

1. Обобщенные координаты.

2. Принцип наименьшего действия в классической механике. Уравнения движения Лагранжа.

3. Функция Лагранжа простейших систем.

4. Законы сохранения.

5. Обобщенный импульс.

6. Канонически сопряженные величины.

7. Функции Гамильтона простейших систем.

8. Колебания системы с одной степенью свободы.

9. Характеристическое уравнение.

10. Уравнения Максвелла для электромагнитного поля в вакууме.

11. Потенциалы электромагнитного поля в вакууме.

12. Градиентная инвариантность.

13. Уравнения Максвелла для квазистационарного электромагнитного поля .

14. Условие квазистационарности поля и глубина его проникновения.

15. Уравнения Максвелла для электромагнитных волн в вакууме.

16. Волновое уравнение.

17. Плоская монохроматическая волна.

Экзаменационные задачи по курсу «Теоретическая механика и теория поля».(план минимум)

1. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

2. Определить скобки Пуассона, составленные из компонент М.

3. Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара . Объемная плотность заряда равна , радиус шара R.

4. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью j. Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

5. Показать, что постоянное однородное магнитное поле B можно описывать векторным потенциалом А=.

68