[§41.] Плоская монохроматическая волна.

Если волна монохроматическая, то - волна одной частоты .

Введём параметр - волновое число.

Введём волновой вектор , направленный по нормали к фронту волны. Тогда:

- плоская монохроматическая волна, идущая вдоль вектора .

§42. Уравнения Максвелла в случае плоской монохроматической волны в вакууме.

Уравнения Максвелла в случае электромагнитных волн в вакууме имеют вид:

Т.к. поля и имеют зависимость ~, то

где , тогда:

В результате для плоских монохроматических волн операторы:

Тогда уравнения Максвелла для плоских монохроматических волн имеют вид:

вводим единичный вектор , тогда

Тогда векторы создают правовинтовую систему. Здесь - вектор нормали к фронту распространения волны.

§43. Разложение электромагнитных полей по плоским монохроматическим волнам.

Разложим :

где , а - амплитуда данной монохроматической волны, присутствующей в электромагнитном поле, т.е. это вес волны.

§44. Калибровка Лоренца в случае однородной изотропной среды.

Калибровка Лоренца в случае вакуума:

В случае однородной изотропной среды калибровка Лоренца примет вид:

Задачи по курсу «Теоретическая механика и теория поля»

[1.] Наити функцию Лагранжа двойного плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g).

2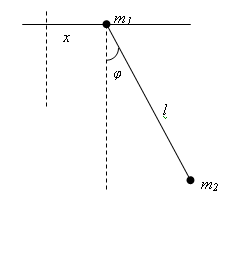. Найти функцию Лагранжа плоского маятника, находящегося в однородном поле тяжести (ускорение силы тяжести g) с массой m2, точка которого (с массой m1 в ней) может совершать движения по горизонтальной прямой.

[3.] Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.

[4.] Определить скобки Пуассона, составленные из декартовых компонент импульса р и момента импульса материальной частицы.

5. Определить скобки Пуассона, составленные из компонент М.

6*. Показать, что =0, , где φ – любая скалярная функция координат и импульса частицы.

7*. Показать, что =fn, где f – векторная функция координат и импульса частицы, а n – единичный вектор в направлении оси z.

8. Выразить амплитуду и начальную фазу колебаний через начальные значения x0, v0 координаты и скорости.

9. Найти частоту колебаний точки с массой m, способной двигаться по прямой и прикреплённой к пружине, другой конец которой закреплён в точке А на расстоянии l от прямой. Пружина, имея длину l, натянута с силой F.

10. Найти частоту колебаний изображенного на рисунке 4 маятника, точка подвеса которого (с массой m1 в ней) способна совершать движение в горизонтальном направлении.

11. Определить малые колебания двойного плоского маятника.

12. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

13. Вычислить где p – постоянный вектор.

14. Пользуясь теоремой Остроградского-Гаусса, вычислить интегралы: если объем, который охватывает замкнутая поверхность, равен V; A – постоянный вектор.

15. В равномерно заряженном шаре с объемной плотностью заряда имеется шарообразная полость, центр которой расположен на расстоянии а от центра шара. Найти напряженность электрического поля внутри полости, внутри шара и снаружи шара. Радиусы шара и полости равны соответственно R и .

[16.] Определить напряженность электрического поля внутри и снаружи равномерно заряженного шара . Объемная плотность заряда равна , радиус шара R.

17. Определить коэффициенты разложения потенциала точечного заряда в интеграл Фурье.

18. Найти потенциал, создаваемый зарядом, распределенным в бесконечной среде по закону :

19. Определить потенциал точечного заряда е, находящегося в однородной анизотропной среде с заданным тензором диэлектрической проницаемости.

20. Найти напряженность магнитного поля внутри цилиндрической полости цилиндрического проводника, по которому течет ток, равномерно распределенный по его сечению с плотностью j. Оси цилиндра, образующего полость, и цилиндрического проводника параллельны и находятся друг от друга на расстоянии а.

[21.] Показать, что постоянное однородное магнитное поле B можно описывать векторным потенциалом А=.